Вариант 1
1.
С помощью двойного интеграла вычислить
площадь фигуры, ограниченной линиями
.
2.
Определить массу пирамиды, образованной
плоскостями
,
,
если плотность в каждой точке равна
аппликате этой точки.
3.
Пользуясь формулой Остроградского,
вычислить
,
где S
– внешняя сторона поверхности пирамиды,
ограниченной плоскостями
4.
Найти циркуляцию вектора
по окружности
.
Вариант 2
1.
Найти массу тела, ограниченного
поверхностями
,
если плотность в каждой точке равна
аппликате этой точки.
2.
Вычислить
,
где L
– верхняя половина окружности
.
3.
Выяснить, будет ли интеграл
зависеть от пути интегрирования и
вычислить его по линии AB,
соединяющей точки
.
4.
Вычислить
,
где S
– внешняя сторона треугольника,
образованного пересечением плоскости
и координатными плоскостями.
Вариант 3
1.
Изменив порядок интегрирования, записать
данное выражение в виде двойного
интеграла
.
Вычислить интеграл.
2.
Найти массу дуги кривой
,
если плотность в каждой точки равна
квадрату ее абсциссы.
3.
Вычислить
,
где L
– дуга параболы
,
расположенная над осью
,
пробегаемая по ходу часовой стрелки.
4.
Применяя формулу Остроградского,
вычислить
,
где S
– внешняя сторона поверхности, образуемой
плоскостями
.
Вариант 4
1.
Найти массу половины круга R
с центром в начале координат, лежащей
в области
,
если плотность равна квадрату полярного
радиуса.
2.
Вычислить объем тела, ограниченного
поверхностями
.
3.
Вычислить
,
где L
– отрезок прямой между точками
и
.
4.
Найти площадь поверхности части конуса
,
заключенного внутри цилиндра
.
Вариант 5
1. Вычислить объем тела, ограниченного поверхностями .
2.
Вычислить массу дуги кривой
,
лежащей в первой четверти, если плотность
в каждой ее точки равна абсциссе этой
точки.
3.
Найти массу полусферы
,
если поверхностная плотность в каждой
точке пропорциональна квадрату расстояния
этой точки до начала координат.
4.
Найти циркуляцию векторного поля
вдоль замкнутого контура, полученного
от пересечения сферы
координатными плоскостями в первом
октанте.
Вариант 6
1. С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями .
2.
Вычислить массу тела, ограниченного
поверхностями
,
если плотность в каждой точке
пропорциональна ординате этой точки.
3.
Вычислить
,
где L
– дуга кривой
.
4.
Вычислить поток вектора
через поверхность шара
.
Вариант 7
1.
Найти площадь фигуры, ограниченной
линиями
и
(вне параболы).
2.
Вычислить массу тела, ограниченного
поверхностями
,
если плотность в каждой точке равна
аппликате точки.
3.
Вычислить
по отрезку прямой
от точки
до точки
.
4.
Вычислить поток вектора
через поверхность шара единичного
радиуса с центром в начале координат.
Вариант 8
1.
Найти массу фигуры, ограниченной линиями
,
если плотность ее в каждой точке равна
ординате этой точки.
2.
Найти объем тела, ограниченного
поверхностями
и расположенного в первом актанте.
3.
Вычислить
,
где L
– кривая,
.
4.
Вычислить
,
где S
– внешняя сторона поверхности куба,
ограниченного плоскостями
.
Вычислить непосредственно и с помощью
формулы Остроградского
Вариант 9
1.
Построить
область, площадь которой выржается
интегралом
.
Вычислить этот интеграл. Поменять
порядок интегрирования.
2.
Определить объем тела, ограниченного
поверхностями
,
если плотность в каждой точке
пропорциональна аппликате этой точки.
3. Вычислить , где l – дуга кривой .
4.
Вычислить
,
где S
– внешняя сторона поверхности
,
отсеченной плоскостями
.
Вариант 10
1.
Найти объем тела, ограниченного
поверхностями
2.
Вычислить
по параболе
от точки
до точки
.
3.
Вычислить
,
применяя формулу Грина, где
– контур треугольника с вершинами в
точках
,
,
,
пробегаемый против часовой стрелки.
4.
Вычислить
,
где
– поверхность конуса
,
ограниченного плоскостью
.
Вариант 11
1. С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями .
2.
Определить массу сферического слоя
между поверхностями
,
если плотность в каждой точке обратно
пропорциональна расстоянию точки от
начала координат.
3.
Вычислить массу поверхности
,
ограниченной плоскостями
,
если поверхностная плотность в каждой
точке равна абсциссе этой точки.
4.
Найти циркуляцию вектора
по замкнутой кривой, составленной из
верхней половины эллипса
и отрезка оси Ох.
Вариант 12
1.
Вычислить
где область D
ограничена
прямыми
.
2. Вычислить объем тела, ограниченного поверхностями .
3.
Вычислить массу дуги кривой
от t
= 0 до t
= 1, если
плотность равна
.
4.
Вычислить массу поверхности
,
заключенной между плоскостями
,
если поверхностная плотность
пропорциональна
.
Вариант 13
1.
Вычислить
где
- область, ограниченная цилиндром
и плоскостями
.
2.
Найти массу дуги
,
если плотность в каждой ее точке обратно
пропорциональна абсциссе этой точки:
.
3.
Применяя формулу Грина, вычислить
,
где С
– окружность
(в положительном направлении).
4.
Найти площадь поверхности
,
расположенной над плоскостью хОу.
Вариант 14
1.
Определить объем тела, ограниченного
поверхностями
.
2.
Найти массу дуги винтовой линии
,
если плотность ее в каждой точке
пропорциональна аппликате этой точки:
.
3.
Вычислить
.
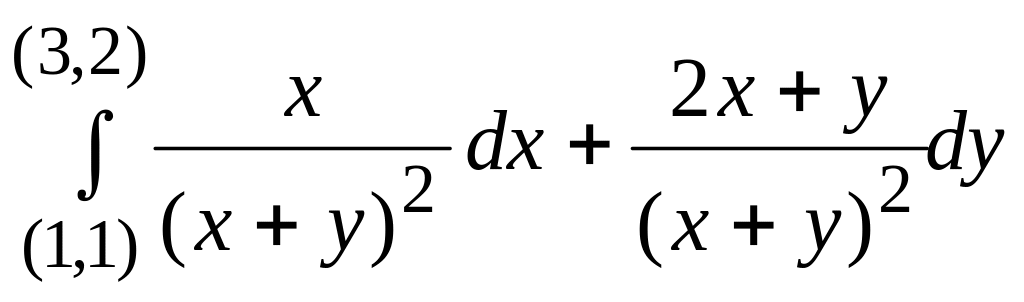4.
Используя формулу Остроградского,
вычислить
через поверхность шара
.
Вариант 15
1.
Определить массу полушара
,
если плотность его в каждой точке равна
аппликате этой точки.
2.
Вычислить
,
где L
– дуга кривой
от
до
.
3.
Вычислить
,
где С
– треугольник, сторонами которого
являются прямые
.
Доказать, что данный интеграл по любому
замкнутому контуру равен нулю.
4.
Найти площадь части поверхности
,
вырезанной цилиндром
и расположенной в первом октанте.
Вариант 16
1.
Вычислить
,
где область D
– кольцо между окружностями радиусов
e и
1
с центром в начале координат.
2.
Вычислить массу тела, ограниченного
поверхностями
если плотность в каждой точке равна
абсциссе этой точки.
3.
Вычислить
,
где S
– верхняя сторона поверхности
,
отсеченная плоскостями
4.
Найти циркуляцию поля
по окружности
.
Вариант 17
1.
Вычислить
,
где D
– круг
2.
Вычислить массу одной арки циклоиды
если плотность в каждой точке кривой
равна ординате точки.
3.
Вычислить
от точки А(0,
0) до точки В(1,
2) по кривой
.
4.
Вычислить с помощью формулы Остроградского
,
где S–внешняя
поверхность тела, ограниченного
поверхностями
Вариант 18
1.
Вычислить площадь фигуры, ограниченной
линиями
