
- •1 Краткое описание алгоритмов
- •1. Формирование математической модели
- •2. Графический метод решения задач линейного программирования
- •3. Решение математических задач симплексным методом
- •5. Решение двойственной задачи
- •6. Построение опорных планов шестью методами
- •7. Проверка опорного плана на оптимальность методом потенциалов
- •8. Метод дифференциальных рент
- •9. Решение задач о кратчайших расстояниях
- •10. Сетевое планирование и управление
- •12. Решение задач оптимальной загрузки оборудования
- •13. Задача оптимального раскроя
- •14. Решение задач оптимальной очерёдности обработки деталей
- •15. Решение задач выбора венгерским методом
- •2 Подробное изложение алгоритмов
- •2.1 Формирование математической модели
- •2.2 Графический метод решения задач линейного программирования
- •2.3 Решение математических задач симплексным методом
- •2.5 Решение двойственной задачи
- •2.6 Построение опорных планов шестью методами
- •2.7 Проверка опорного плана на оптимальность методом потенциалов
- •2.8 Метод дифференциальных рент
- •2.9 Решение задач о кратчайших расстояниях
- •2.10 Сетевое планирование и управление
- •2.12 Решение задач оптимальной загрузки оборудования
- •2.13 Задача оптимального раскроя
- •2.14 Решение задач оптимальной очерёдности обработки деталей
- •2.15 Решение задач выбора венгерским методом
2.8 Метод дифференциальных рент
В каждом столбце матрицы определяется и выделяется наименьшее Cij. Затем, начиная с первого столбца, в выделенные клетки заносятся максимально возможные поставки (см. Таблица 35). Если при распределении в выделенной клетке не остаётся ни мощности, ни спроса, то заносится нулевая поставка.
По окончании распределения проверяется, исчерпана ли мощность и удовлетворен ли спрос. В этом случае задача решена. В противном случае вычисляются небалансы и знаки строк.
Если вся мощность распределена, а спрос в выделенных клетках строки не удовлетворен, то строка считается отрицательной (при этом поставщик считается недостаточным). В последний столбец заносится недостающий спрос со знаком «-», строка считается отрицательной.
Если спрос во всех выделенных клетках строки удовлетворен, а мощность не исчерпана, то строка считается положительной (при этом поставщик считается избыточным). В последний столбец заносится избыточная мощность со знаком «+», строка считается положительной.
Суммарный неудовлетворённый спрос должен быть равен суммарной нераспределенной мощности, это называется нераспределенным остатком. Суммарные небалансы заносятся в последнюю клетку последнего столбца.
В каждом столбце определяется разность между наименьшим Cij в положительной строке и выделенным Cij, эта разность записывается в последнюю строку. Данная разность не определяется в тех столбцах, в которых хотя бы один выделенный элемент находится в положительной строке. Выделяется наименьшая разность, она называется промежуточной рентой.
Таблица 35 – Первая таблица поставок
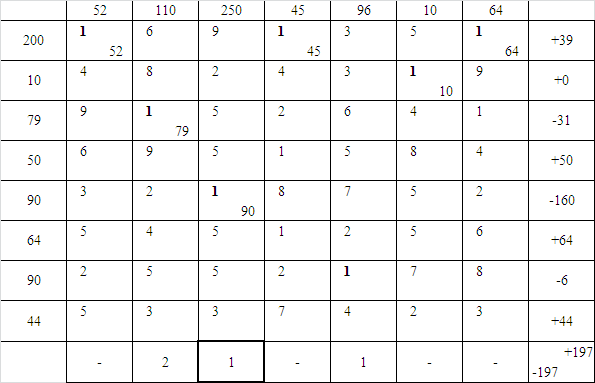
Составляется новая таблица (см. Таблица 36), в которую все Cij в положительных строках переносятся без изменений, а ко всем Cij в отрицательных строках прибавляется промежуточная рента.
В одной из бывших положительных строк определяется и выделяется Cij, равное числу, выделенному в этом столбце.
В новой таблице нужно пронумеровать выделенные клетки. Присвоить номер можно только той клетке, которая является единственной выделенной клеткой в столбце или строке. При нумерации каждой последующей выделенной клетки критерий чередуется: если первой пронумерована единственная в столбце выделенная клетка, то следующей нумеруется единственная в строке выделенная клетка, потом – в столбце, потом – в строке и, так далее, пока не будут пронумерованы все выделенные клетки. После этого вносятся поставки, строго придерживаясь нумерации.
Таблица 36 – Вторая таблица поставок

На каждой итерации добавляется одно и только одно выделенное число (см. Таблица 37, Таблица 38, Таблица 39, Таблица 40, Таблица 41, Таблица 42, Таблица 43, Таблица 44). Исключение: если в столбце появляются два выделенных числа, не равных друг другу, то убирается выделение того числа, которое было в отрицательной строке.
Небалансы от итерации к итерации уменьшаются до нуля или остаются неизменными. Нулевой небаланс свидетельствует о том, что план допустимый, задача решена.
При нулевом небалансе строки нуль является положительным, если строка связана с другой положительной строкой, и отрицательным, если строка связана с другой отрицательной строкой.
Таблица 37 – Третья таблица поставок
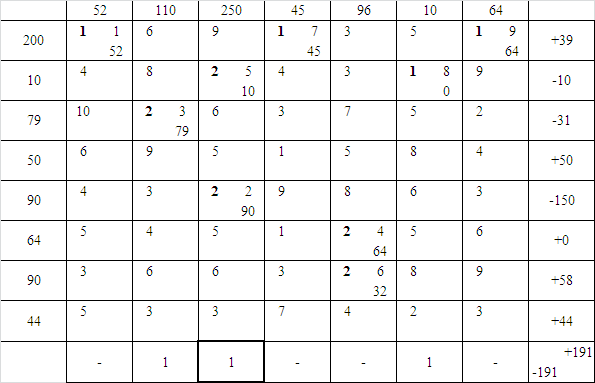
Таблица 38 – Четвёртая таблица поставок

Таблица 39 – Пятая таблица поставок
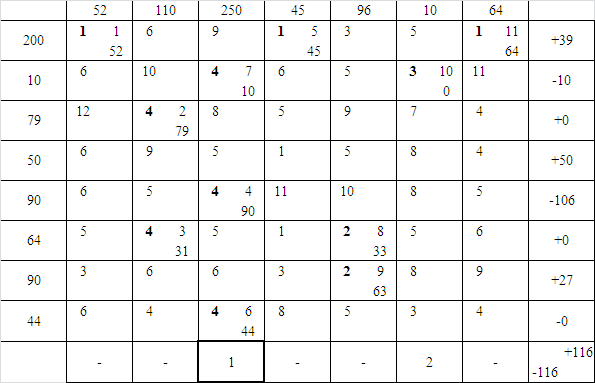
Таблица 40 – Шестая таблица поставок
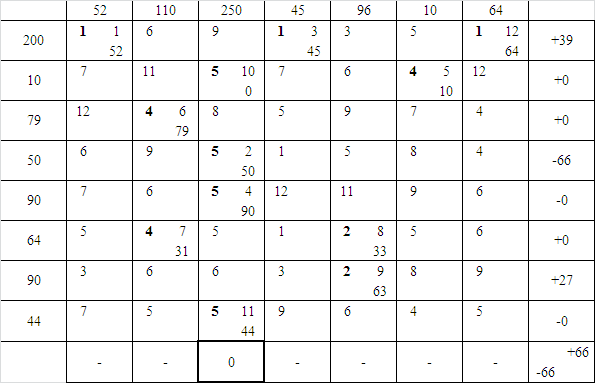
Таблица 41 – Седьмая таблица поставок
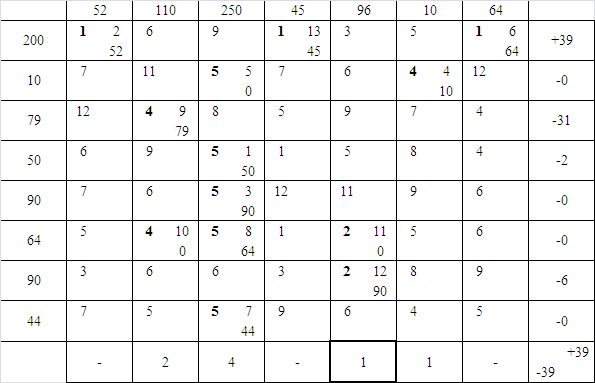
Таблица 42 – Восьмая таблица поставок

Таблица 43 – Девятая таблица поставок

Таблица 44 – Последняя таблица поставок
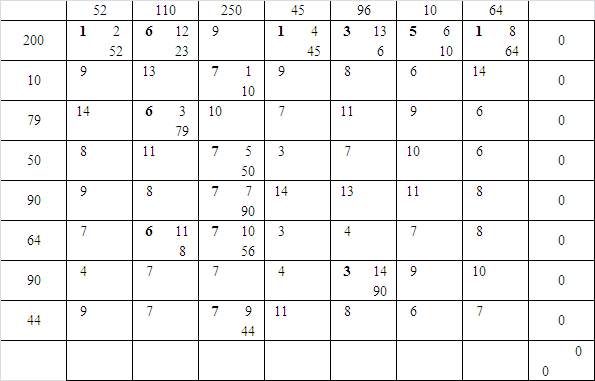
Fmin=1*52+2*23+…+3*44=1348
