13. Задача оптимального раскроя
Несколько видов деталей вырезаются из рулонов листовой стали. Известны размеры деталей и рулонов. Требуется изготовить определённое количество деталей при наименьших затратах. Определяется семь вариантов раскроя. Количество стальных отходов составляет целевую функцию, которую нужно минимизировать. Из требуемого количества деталей и параметров раскроя составляются ограничивающие уравнения. Далее задача решается симплексным методом.
14. Решение задач оптимальной очерёдности обработки деталей
Даны два станка (А и В) и некоторое количество деталей. Сначала каждая деталь обрабатывается на станке А, а затем - на станке В. Известно время обработки каждой детали на каждом станке. Если обработка детали на станке А уже завершилась, а обработка предыдущей детали на станке Б ещё продолжается, то возникает простой. Нужно организовать порядок обработки деталей так, чтобы общий простой был минимальным. Для этого используется алгоритм Джонсона: в зависимости от времени обработки детали на том или ином станке она перемещается в начало или конец очереди, в результате общий простой уменьшается.
15. Решение задач выбора венгерским методом
Изначально имеется квадратная матрица. На предварительном этапе получается новая матрица, в каждой строке и в каждом нуле которой есть нуль. От итерации к итерации добавляется по одному независимому нулю. Каждая итерация начинается с первого и заканчивается вторым этапом, между которыми может быть произвольное число третьих этапов. Задача считается решённой, когда количество независимых нуле равно количеству столбцов матрицы.
2 Подробное изложение алгоритмов
2.1 Формирование математической модели
Требуется перевезти некоторое количество единиц однородного товара из различных складов к нескольким магазинам. Каждому из этих магазинов требуется определённое количество товаров. Каждый из складов может выделить определённое количество товаров. Вводятся следующие обозначения (см. Таблица 1):
m – количество складов
n – количество магазинов
ai – общее количество единиц товара на i-ом складе
bj – количество единиц товара, необходимого j-му магазину
xij – количество единиц товара, доставляемого с i-го склада в j-ый магазин
Предполагается, что Σai= Σbj.
Требуется определить xij - сколько товара доставить с каждого склада в каждый магазин.
Таблица 1 – Условные обозначения
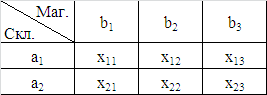
Система ограничений |
{ |
a1=x11+x12+x13 a2=x21+x22+x23 b1=x11+x12 b2=x12+x22 b3=x13+x23
|
cij – стоимость перевозки единицы товара из i-го склада в j-ый магазин, предполагая, что зависимость стоимости перевозки от количества товара линейная.
Требуется составить такой план перевозок, чтобы денежные затраты были минимальные.
Целевая функция:
C11*x11+
C12*x12+
C13*x13+
C21*x21+
C22*x22+
C23*x2==>Fmin
При этом xij>=0:
Система ограничений |
{ |
x11>=0 x12>=0 x13>=0 x21>=0 x22>=0 x23>=0 |
2.2 Графический метод решения задач линейного программирования
Коэффициенты при неизвестных целевой функции являются координатами вектора C, исходящего из начала отсчёта.
Zmin=8x1+4x2
На основании каждого ограничения строится прямая, выделяющая две полуплоскости.
{ |
2x1-3x2<=2 3x1-x2<=-2 5x1+2x2>=25 |
x1>=0, x2>=0
Областью решения является общее значение всех полуплоскостей.
Далее строится перпендикуляр, после чего нужно двигаться по направлению вектора, пока последняя точка A области решения не коснется перпендикуляра (см. Рисунок 1). Если область решений неограниченна, то решений нет.
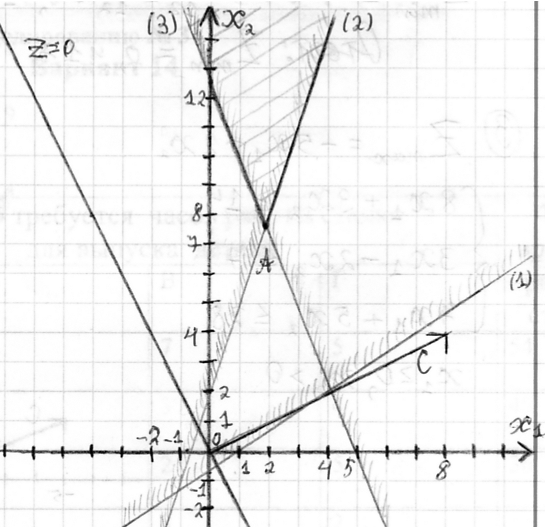
Рисунок 1 – Итоговые графики
Затем определяются координаты найденной точки, для этого при необходимости составляется система уравнений.
Далее определяется значение целевой функции в этой точке.
Zmin=8*1,91+4*7,73=46,18
Полученное значение является ответом.