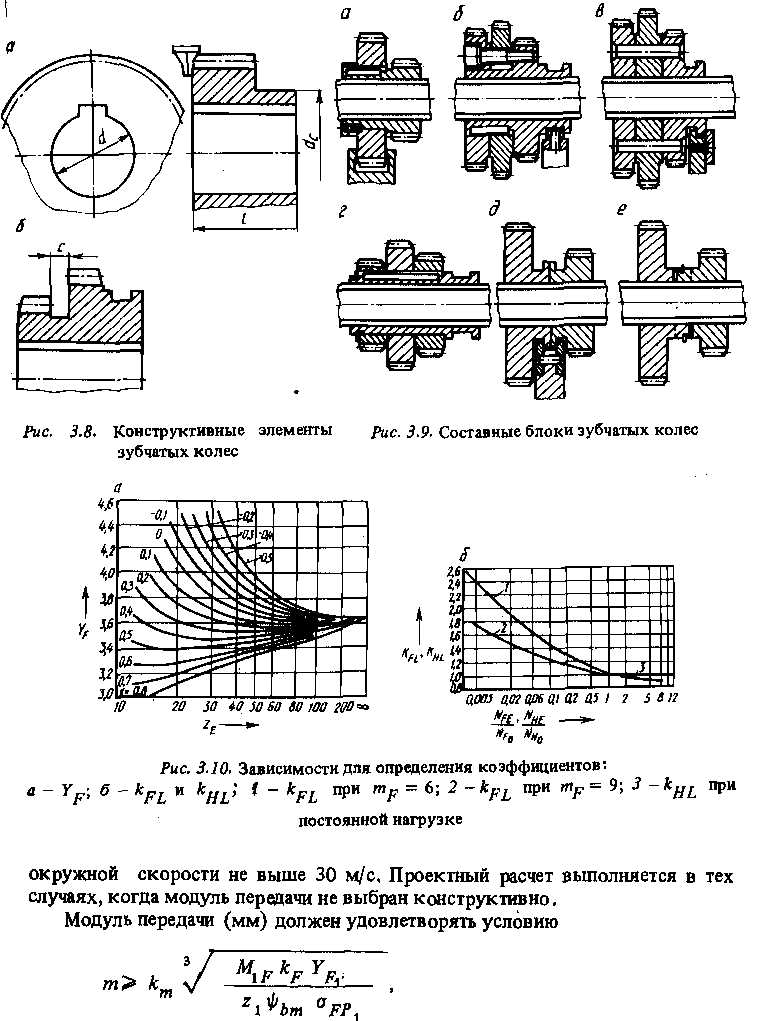
3.4. Цилиндрические зубчатые передачи

Конструкции зубчатых колес. Шлифованные или хонингованные стальные прямозубые колеса можно применять при окружной скорости передачи до 16 м/с, косозубые — при скорости до 30 м/с. Нешлифованные прямозубые ко­леса пригодны, когда окружная скорость передачи не выше 6 м/с, косозу­бые - до 16 м/с. Передаточное число цилиндрической передачи в главном при­воде станка должно находиться в интервале от 0,25 до 2,в приводе подачи — от 0,2 до 2,8.

Число зубьев некоррегированного зубчатого колеса должно быть не меньше 18. Ширину венца принимают равной 6—10 модулям (меньше для подвиж­ных колес). Во избежание поломок колес толщина стенки между шпоночным пазом и впадиной зуба должна быть больше двух модулей. Диаметр ступицы d_c.обычно равен 1,6d (рис. 3,8,а). Длину I выбирают исходя из необходимости обеспечить прочность шпоночного или шлицевого соединения колеса с ва­лом, снизить габариты и массу узла, а также с учетом соотношения 0,8d ≤ l ≤..1,5d.

В цельных блоках зубчатых колес предусматривают выточку для выхода долбяка шириной с (рис. З.8.б):

Модуль колеса, мм 1...2 2,5.,4 4.„5

с,мм 5 6 7

Составные блоки по сравнению с цельными имеют меньшую длину и массу, В них можно соединять колеса из разных материалов, со шлифованными венцами. При ремонте допускается замена только одного вышедшего из строя венца. Венцы составных блоков, работающие при импульсных нагрузках (в приводах фрезерных станков), более долговечны, что объясняется их самоустановкой благодаря коротким ступицам и более равномерному распределе­нию нагрузки по длине зуба.

Ряд способов соединения зубчатых колес в составные блоки приведен на рис. 3,9. Насадное колесо может быть помещено на ступице основного, в ка­честве которого используется колесо меньшего диаметра (рис.3.9,а, б).Кру­тящий момент на насадное колесо передается шпонкой, цилиндрическими штифтами, зубчатой муфтой, В осевом направлении оно фиксируется установочным винтом, пружинным кольцом, винтом. Колеса могут быть установле­ны непосредственно на валу (рис, 3,9, в, д, е) и соединены между собой с по­мощью развальцованных штифтов, охватывающей составной вилки, пружин­ного кольца, резьбы. Колеса составного блока могут быть установлены на об­щей втулке (рис. 3.9, г). Этот способ применяется, когда у насадных колес нет ступиц, а наименьшие из них имеют значительное число зубьев.

Зубчатые колеса с венцом, приклеенным к ступице, экономически эффек­тивны, когда их венцы изготовляются централизованно, а ступицы индиви­дуально.

Проектный расчет цилиндрических зубчатых передач на выносливость зубьев при изгибе. Изложенная ниже методика соответствует отраслевому руководящему материалу [ 82] ■ Она пригодна для расчета стальных силовых цилиндрических зубчатых колес с модулем 1,5-.12 мм, образующих передачи внешнего зацепления, работающие в закрытых корпусах со смазыванием при

где к_m — вспомогательный коэффициент; к_m = 13 для прямозубых передач, к_т= 12 для косоэубых; M_lF — исходный расчетный крутящий момент на шестерне; k_F — коэффициент нагрузки для шестерни: меньшие значения относятся к зубчатому колесу, расположенному между опорами сим­метрично; Y_F1- коэффициент, учитывающий форму зуба и выбираемый по рис. 3. 10, а в зависимости от эквивалентного числа зубьев (для прямозубых колес z_E = z); z₁. - число зубьев шестерни; ψ_bm - отношение ширины колеса b к модулю т ; σ_FP1 - допускаемое напряжение для мате­риала шестерни, МПа.

Допускаемое напряжение на изгиб (МПа) (3.1).

где . σ_{Flim b}.— предел выносливости материала зубьев, МПа (табл. 3.13);

k_FL. - коэффициент режима нагружения и долговечности, учитывающий влия­ние режима нагружения на длительный предел выносливости при изгибе:

m_F.- показатель кривой усталости; N_F0.- — базовое число циклов перемены напряжений при изгибе; N_fE — эквивалентное число циклов перемены напря­жений. Для зубчатых колес, подвергаемых цементации или нитроцементации, принимают для зубчатых колес с другой термообработкой Если при частоте вращения п._i (об/мин) зубчатое колесо работает в течение t_i. часов, за расчетный срок службы пе­редачи t_∑ суммарное число циклов перемены напряжений в зубе

Если нагрузка постоянна, принимают. N_FE = N_∑ . Если же нагружение сту­пенчатое и при нагрузке М _1i число циклов перемены напряжений в зубе рав­но п_{ц i}.

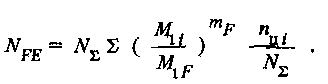
Если .коэффициент к_FL.,определяют по графику (рис. 3.10, б).

о

При берут (если т_р = 9) или ( если m_F =6). При принимают Значения к_FL для других случаев приведены в [82].

Для реверсивных зубчатых передач допускаемое напряжение уменьшают на 25 % по сравнению с вычисленным по зависимости (3.1)

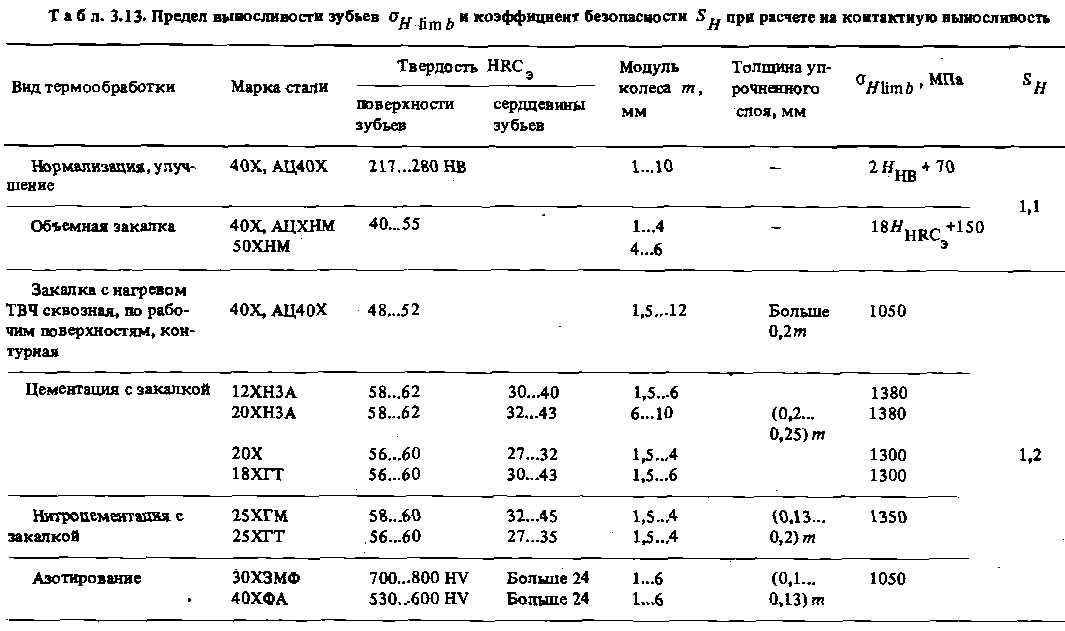
Проектный расчет передач на контактную выносливость зубьев. Исходя из заданного передаточного числа u (u≥ 1) и отношения ψ_bd . рабочей ширины венца передачи b_w к начальному диаметру шестерни .d_w1 определяют, соблюдается ли соотношение

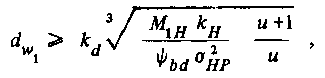
где к. - вспомогательный коэффициент; k_d = 770 для прямозубых пере­дач, .k_d = ЗбО для косозубых передач; к_н —коэффициент нагрузки:

Допускаемое контактное напряжение для прямозубых передач опреде­ляют раздельно для шестерни и колеса по зависимости

(3.2)

Здесь σ_{Hlim b}.— базовый предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов перемены напряжений (табл. 3.13); .S_H - коэффициент безопасности (табл. 3.13).

В качестве допускаемого контактного напряжения для косозубой переда­чи принимают условное напряжение

Проверочный расчет цилиндрических зубчатых передач на выносливость зубьев при изгибе. Удельная расчетная окружная сила (Н)

где F_Ft - расчетная окружная сила, Н; b - ширина венца по основанию зуба; k_Fv - коэффициент, учитывающий динамическую нагрузку в зацеплении, которая возникает вследствие колебаний масс колес и ударов в зацеплении (табл, 3.14); к_Fβ. - коэффициент, учитывающий неравномерность распределе­ния нагрузки по ширине венца, которая возникает вследствие погрешностей изготовления колес, упругих деформаций валов, зазоров в подшипниках (табл. 3.15); к_Fa.- коэффициент, учитывающий при расчете косозубых передач распределение нагрузки между зубьями: к_Fa. = 0,7...0;9, если коэффициент осевого перекрытия колес берут равным у _β для прямозубых колес, если ε_β ≤ 1; M_lF- расчетный крутящий момент, Н-м; d₁-делительный диаметр шестерни, мм.

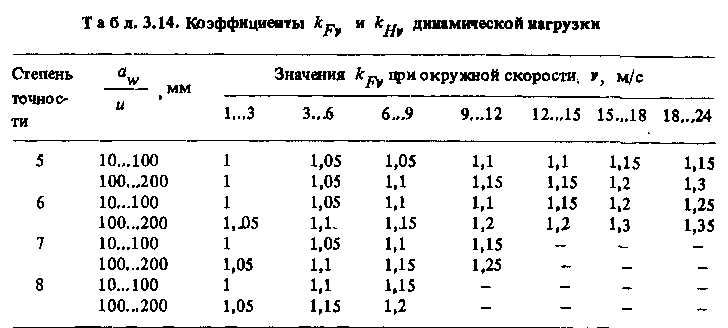
Примечания: 1. Коэффициенты к_Fv приведены для нормально и тяжело нагруженных зубчатых передач {F_t / b.> 50 Н/мм).

2. Значения k_Fv для косозубых колес следует определять путем уменьшения в 2 раза динамической надбавки, учитываемой для прямозубых колес, Например, если для прямозубых колес к_Fv = 1,2, то для косозубых к_Fv = 1,1,

3. Коэффициенты к_Ну для прямозубых колес, имеющих зубья с твердостью поверхностей H₁ > 350 НВ и Н_г > 350 НВ, совпадают с коэффициентами к_Fv.

2. Коэффициенты к_Ну для прямозубых колес при Н₂ < 350 следует определять уменьшением в 2 раза динамической надбавки, взятой по таблице.

3. Коэффициенты к_Ну для косозубых колес gри Н₁ > 350 НВ и Н.₂> 350 НВ следует определять уменьшением в 2 раза динамической надбавки, взятой по таблице, в при Н₂ < 350 -уменьшением этой надбавки в 4 раза.

Расчетное напряжение изгиба зубьев

где Y_F — коэффициент формы зуба; Y_ε — коэффициент, учитывающий пере­крытие зубьев при расчете прямозубых передач (первоначально принимают Y_ε = 1 и таким образом напряжение определяют в предположении, что нагруз­ка передается одной парой зубьев); Y_β. — коэффициент, учитывающий наклон

зуба при расчете косозубых передач: Y_β= 1 — β/140.

Допускаемое напряжение при расчете зубьев на выносливость при изгибе

(3.3)

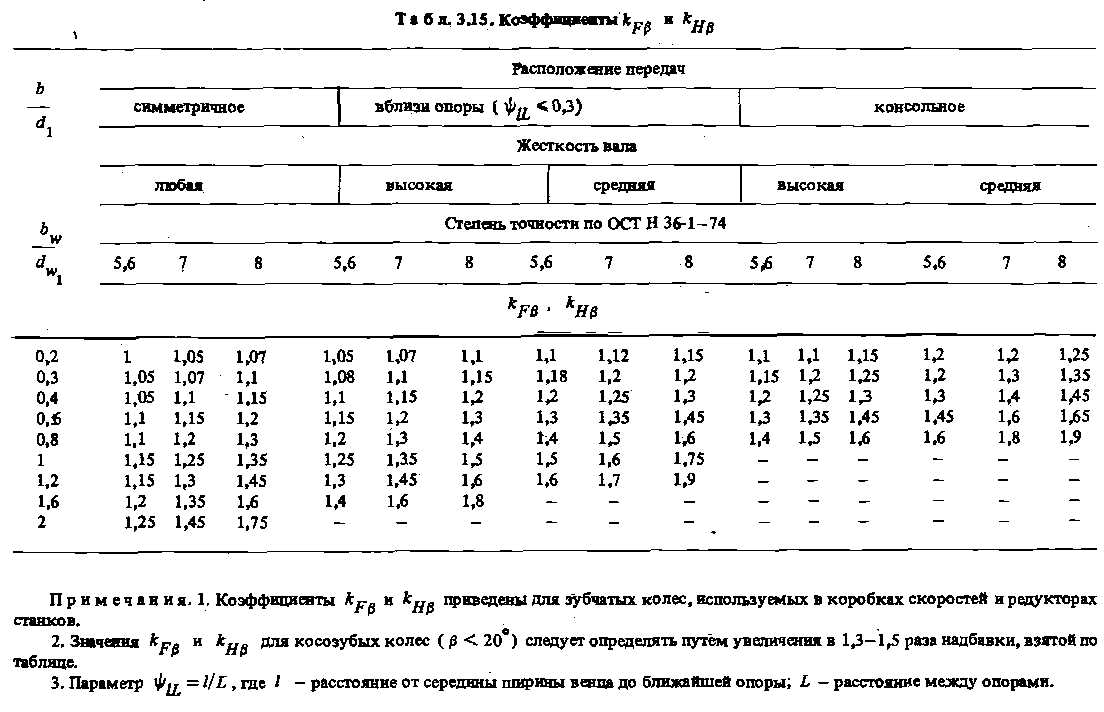
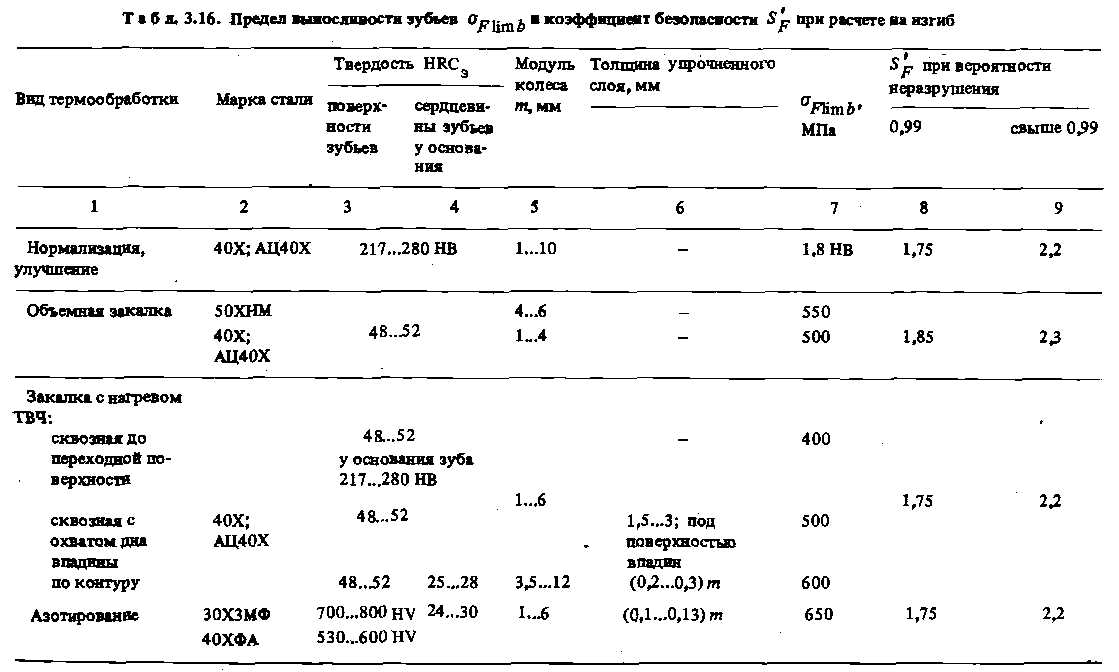
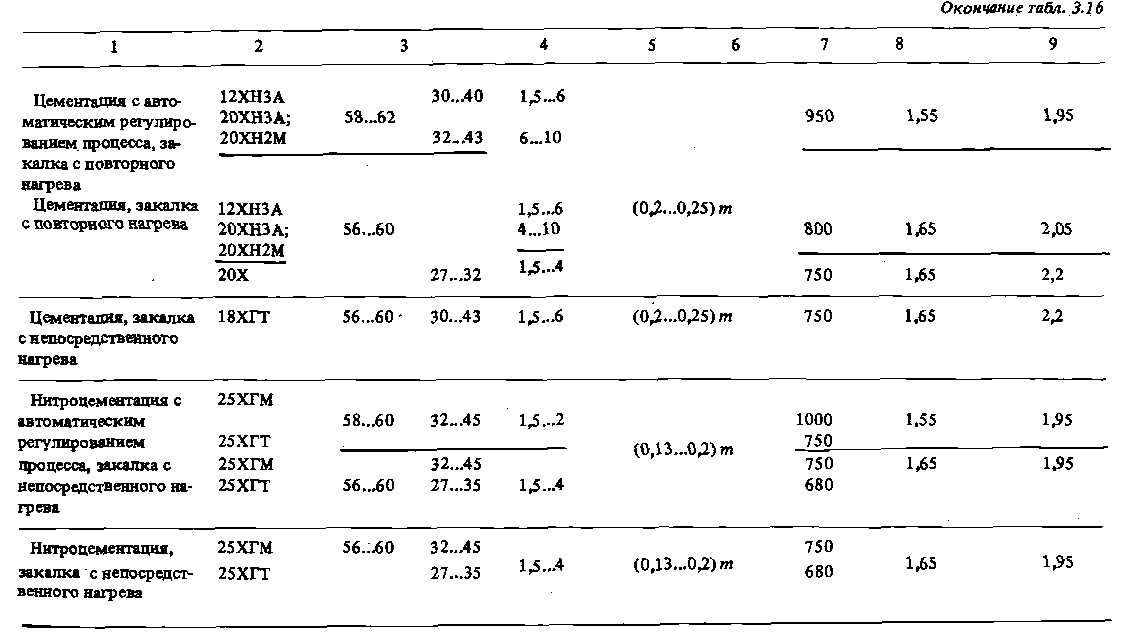
где. σ _{Flim b}.— - длительный предел выносливости зубьев при изгибе,соответст­вующий базовому числу от нулевых циклов перемены напряжений (табл. 3.16); к_Fg. - коэффициент, учитывающий влияние шлифования переходной поверхности зубьев: для нешлифованных зубьев принимают к_Fg = 1, для шлифованных - по табл. 3.17; к_Fa — коэффициент, учитывающий влияние уп­рочнения переходной поверхности зубьев в результате механической обработ­ки; при отсутствии такого упрочнения принимают к_F._а = 1,для зубьев, уп­рочненных дробью или роликами, - по табл. 3.18; к_Fc - коэффициент, учиты­вающий особенности работы зубьев при передаче реверсивной нагрузки: если нагрузка действует одинаково в противоположных направлениях, то для азо­тированных колес к_Fc = 0,85, для других колес к_Fc = 0,65...0,75; к_xF —коэффициент, учитывающий размеры зубчатого колеса: к_хF = 1 при d ≤ 300мм; к_x._F = 1...1.2 (d_a - 300)-10 ^-4 при 300 мм < d_a.<2000мм;

k_FL ~ коэффициент режима нагружения и долговечности; Y_s - коэффи­циент, отражающий чувствительность материала зубьев к концентрации напря­жений; Y_s = l,lm ^-0,09; Y_R — коэффициент, учитывающий параметры шероховатости переходной поверхности зуба: Y_R = 1,1.,.1,3 в случае шлифованной поверхности; Y_R = 1 в других случаях; S_p - коэффициент безопас­ности: S_p = S'_F. S,”_F (S'_F - коэффициент безопасности, учитывающий неста­бильность свойств материала зубчатого колеса и ответственность зубчатой пе­редачи (табл. 3.16); S'_p - коэффициент, учитывающий способ получения за­готовка зубчатого колеса: 5р = 1 для поковок и штамповок; S_F — 1,15 для заготовок из проката; S"_F = 1,3 для литых заготовок).

Допускаемое напряжение определяют по зависимости (3.3) раздельно для шестерни и колеса. Если хотя бы в одном случае расчетное напряжение σ_F превысит допускаемое, то для зубчатых колес 8-й и более высоких степеней точности проверяют возможность передачи нагрузки более чем одной парой зубьев. Для этого вычисляют параметр

где f_pbw — эффективная (действующая) погрешность основного шага зацеп­ления, мкм (табл. 3.19); b — ширина венца по основанию зуба, мм; F_Ft — исходная удельная окружная сила, Н/мм.

Если λ ≥ 1, то с учетом σ_F > σ_Fp допускают, что усталостный излом зуба возможен. Когда 0,7 ≤ λ < 1, считают, что нагрузка передается более чем одной парой зубьев, и повторно определяют расчетное напряжение при у_е = λ. Если λ < 0,7, то повторный расчет выполняют при λ = 0,7,

Расчет передач на контактную выносливость зубьев. Удельная расчетная окружная сила

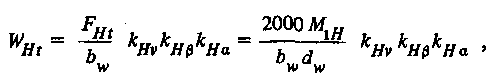
где F_Hl - исходная расчетная окружная сила, Н; к_Ду - коэффициент, учиты­вающий динамическую нагрузку в зацеплении (см.табл, 3.14); к_н -коэф­фициент, учитывающий неравномерность распределения нагрузки по ширине венца (см. табл. 3.15) ; к_На - коэффициент, учитывающий при расчете косозубых колес распределение нагрузки между зубьями:

и - степень точности зубчатой передачи; v - окружная скорость в зацеплении, м/с; M_1H - исходный расчетный крутящий момент, передаваемый зацепле­нием, Нм; b_w- рабочая ширина венца передачи, мм; d_w - начальный диаметр зубчатого колеса, мм.

Расчетное контактное напряжение

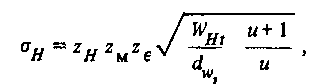
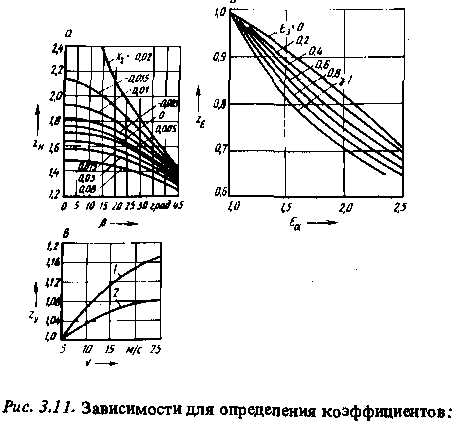
где z_H - коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления и определяемый по рис. 3.11, а в зависимости от угла наклона зубьев β и суммарного коэффициента смещения X_∑ :z_H =- 1,76 для прямозубых передач при а = 20° и Х_∑ = 0; z_M - коэффициент,

учитывающий механические свойства материалов сопряженных зубчатых ко­лес: z_M = 274 для колес из стали с Е₁ =Е_г = 21,5 ∙ 10⁴ МПа; z_e - коэффициент,

учитывающий суммарную длину контактных линий и определяемый по рис. 3.11, б в зависимости от коэффициента торцового перекрытия

и коэффициента осевого перекрытия - передаточное чис — начальный диаметр шестерни, мм.

Допускаемое контактное напряжение для прямозубых передач

где z_R - коэффициент, учитывающий параметр шероховатости поверхностей зубьев; z_R = 1 при R_a ≤ 1,25 мкм, z_R = 0.90…0.95 в остальных случаях; z_v — коэффициент, учитывающий окружную скорость и и определяемый по рис. 3.11, в; k_L, - коэффициент, учитывающий влияние смазочного материа­ла; к_L = 1; к_xH- коэффициент, учитывающий размеры зубчатого колеса;

I ффициент режима нагружения и долговечности:

(3.4)

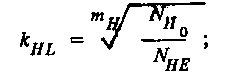
N_H0 базовое число перемены циклов напряжений (рис. 3.12): при твердости поверхностей зубьев более 56 HRC ; N_HE — эквивалентное чис­ло циклов перемены напряжений; при ступенчатом нагружении

при постоянном нагружении N_HE = N_z .

Если коэффициент k_HL определяют по графику на рис. 3.10,6. При N_HE > N_H0 и переменном нагружении k_HL = 1, при постоянном нагружении его определяют по зависимости (3,4), с т_и = 24 (при этом К,, принимают не менее 0,9).