8. Детальное описание отдельных функций
A FUNCTION OF (#,A,B,C,...)
Замечание: Эта функция создается автоматически инструментом построения диаграмм, и ее использование не предполагается при написании уравнений модели
A FUNCTION OF отражает только наличие связей между переменными, она не описывает форму связи и, следовательно, не может быть вычислена. Эта функция недоступна в Редакторе Уравнений. В Текстовом Редакторе за уравнением, использующим функцию A FUNCTION OF, могут следовать одно или два уравнения, содержащие синтаксические ошибки или неполные причинные списки. В отличие от других функций, у функции A FUNCTION OF неопределенное число аргументов.
ACTIVE INITIAL(active eq, initial eq) − различает активные и начальные уравнения.
Эта функция описывает действующее уравнение для вычисления переменной во время имитации, кроме ситуации задания начальных условий − тогда она выдает начальное уравнение. Эта функция обычно используется для разрыва замкнутых циклов вычисления значений переменных.
Замечание: В редакторе формул (Equation Editor) функция ACTIVE INITIAL вводится автоматически, если выбрать тип Auxiliary (Дополнительная переменная) и подтип Initial.
ACTIVE INITIAL (входн. ед., входн. ед.) --> те же ед.
Пример.
Capacity = Integ (capacity adjust, target capacity)
target capacity = Capacity*adjust from utilization
Здесь начальное значение переменной Capacity требует значения переменной target capacity, которое, в свою очередь, требует значения Capacity. Поэтому для переменной target capacity должно использоваться уравнение:
target capacity = ACTIVE INITIAL (Capacity*adjust from utilization, 100)
Это позволит присвоить переменной Capacity начальное значение 100; первое значение target capacity будет равно Capacity*adjust from utilization, т.е. в общем случае не будет равно 100; начальное выражение используется только для вычисления начальных значений переменных состояния (уровней).
DELAY1 (input, delay time) – экспоненциальная задержка.
DELAY1I (input, delay time, initial value) – экспоненциальная задержка с заданным начальным значением.
Значение функции DELAY равно задержанному значению входной переменной. Экспоненциальная задержка первого порядка эквивалентна следующим уравнениям:
DELAY1=LV/delay time
LV=INTEG (input-DELAY1,input*delay time)
Таким образом, если входная переменная input принимает значения 50, 55, 60, и т.д., а время задержки составляет 3, то переменные LV и DELAY1 будут принимать значения:
-
Time
input
LV
DELAY1
0
50
150
50
1
55
150
50
2
60
155
51.6667
3
65
163.3333
54.4444
Функция DELAY1I отличается тем, что можно произвольно задать начальное значение LV:
DELAY1I=LV/delay time
LV=INTEG (input-DELAY1I,initial value*delay time)
См. также: DELAY3, DELAY3I, SMOOTH, SMOOTH3
DELAY1 (ед., время) --> единицы.
DELAY1I (ед., время, ед.) --> единицы.
Единицы измерения входных переменных соответствуют единицам измерения выходных переменных. Время задержки должно быть кратным временному шагу (TIME STEP) и измеряться в тех же единицах. Для функции DELAY1I единицы измерения начальных значений должны соответствовать единицам измерения входной переменной.
DELAY3 (input, delay time) – экспоненциальная задержка третьего порядка.
DELAY3I (input, delay time, initial value) – экспоненциальная задержка третьего
порядка с начальным значением.
Действие функции эквивалентно уравнениям:
DELAY3=LV3/DL
LV3=INTEG (RT2-DELAY3,DL*IN)*)
RT2=LV2/DL
LV2=INTEG (RT1-RT2,LV3)
RT1=LV1/DL
LV1=INTEG (input-RT1,LV3)
18
DL=delay time/3
*)Для функции DELAY3I это уравнение имеет вид:
LV3=INTEG (RT2-DELAY3I,initial value*DL)
Для единиц измерения справедливы те же ограничения, что и у функции DELAY1. Наглядно действие функции DELAY3 иллюстрирует следующий пример:
S = STEP (10,40)
DS = DELAY3 (S,20)
DSI = DELAY3I (S,20,5)
Функция STEP (10,40) генерирует импульс на 40-м шаге с амплитудой 10. Приводимый ниже график показывает, как трансформируется этот импульс в случае экспоненциальной задержки третьего порядка переменной S с помощью u функции DELAY3 и DELAY3I (c начальным значением 5) (Рис. 13).
Р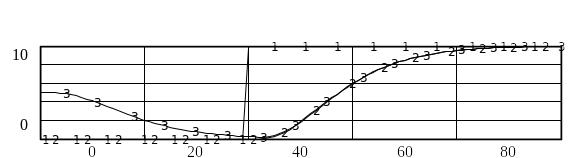
ис.
2. Иллюстрация выполнения функции DELAY3
EXP (X) − то же, что функция POWER (e,X), где e=2.718… EXP (безразмерн.) --> безразмерн. (аргумент должен быть безразмерным).
Примеры:
EXP(1.0) равняется 2.718282
EXP(0.0) равняется 1.0
EXP(-10.0) равняется 4.540E-5
EXP(10.0) равняется 22026.46
EXP(LN(10.0))равняется 10.0 (по определению)