1. Испытания и случайные события.

Испытания и события. Выше событие названо случайным, если при осуществлении определенной совокупности условий S оно может либо произойти, либо не произойти. В дальнейшем, вместо того чтобы говорить «совокупность условий S осуществлена», будем говорить кратко: «произведено испытание». Таким образом, событие будет рассматриваться как результат испытания.

Пример 2. В урне имеются цветные шары. Из урны наудачу берут один шар. Извлечение шара из урны есть испытание. Появление шара определенного цвета — событие.

Виды случайных событий. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. Этот частный случай представляет для нас наибольший интерес, поскольку используется далее.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Пример 4. Стрелок произвел выстрел по цели. Обязательно произойдет одно из следующих двух событий: попадание, промах. Эти два несовместных события образуют полную группу.

2. Сочетания. Число сочетаний и его свойства.

Определение 1. Пусть дано n-элементное множество. Любое k-элементное подмножества множества A называется k-сочетанием n-элементного множества.

Число k-сочетаний n-элементного множества обозначается .

Пример. Выпишем все 2-сочетания 4-элементного множества A={a,b,c,d}: {a;b},{a;c},{a;d},{b,c},{b,d},{c,d}.

Таким образом, .

Теорема 2. при k£n.

Доказательство. Из одного k-сочетания можно получить k! k-размещений n-элементного множества, потому что k элементов можно упорядочить k! способами. Поскольку каждое k-размещение есть не что иное, как упорядоченное k-сочетание, то всего k-размещений будет . С другой стороны k-размещений имеется .

Получили равенство или , и отсюда получаем искомую формулу: . Теорема доказана.

Так, , что согласуется с непосредственным подсчётом 2-сочетаний.

Теорема 3 (простейшие свойства сочетаний).

1)      2)      3)      ;4)      ;5)      , (m³1);

Доказательство.

1) , аналогично .

2) ,

аналогично .

3)      , то есть .

4)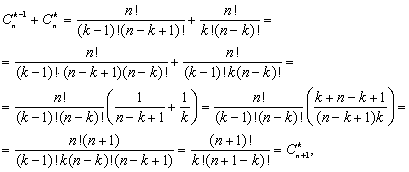 что и требовалось доказать.

5) Это равенство будем доказывать индукцией по m. При m=1 левая часть равна , правая часть равна , то есть при m=1 доказываемое равенство выполняется. Допустим равенство выполняется при m=l , то есть .

Докажем равенство при m=l+1, то есть докажем равенство .

В самом деле,

 (по индуктивному предположению),   по свойству 4). Пятое свойство доказано.

3. Классическое определение вероятности.

При большом числе n испытаний частота P*(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A, т.е. .    Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности).    Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.    Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события.    Очевидно, любое событие A и противоположное ему событие образуют полную группу.    Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A.    Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A.    Пусть события E1,E2, ..., EN в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N. Итак, мы приходим к следующему определению.    Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий: