Мономолекулярные параллельные реакции

Реакции, в которых исходные вещества превращаются одновременно по нескольким направлениям с образованием различных продуктов, называются параллельными. Общая схема такого превращения приведена далее

Скорость всего процесса может быть представлена как

Решение прямой кинетической задачи не составляет большого труда. Запишем дифференциальное кинетическое уравнение через текущую концентрацию

или через плотность глубины реакции

.

П роинтегрируем его :

(4.1)

Линеаризация экспериментальных данных в соответствующих координатах позволит определить сумму констант скоростей .

Выразим уравнение кинетической кривой для исходного вещества А:

.

Общая концентрация продуктов реакции будет равна:

С другой стороны, каждую из реакций можно охарактеризовать плотностями глубин и . Тогда

.

;

отношение концентраций продуктов постоянно и не зависит от времени.

Уравнение материального баланса можно записать как

.

Уравнения (4.2)  (4.4) выражают решение прямой задачи кинетики для параллельной реакции.

Чтобы решить обратную кинетическую задачу, нужно воспользоваться найденным из вышеприведенного рисунка значением суммы констант и соотношением

Если необходимо получить только один продукт, например В, то подбирают экспериментальные условия так, чтобы .

Мономолекулярные последовательные реакции

Это такие реакции, которые состоят из последовательных элементарных стадий. Промежуточные вещества, которые образуются в одной стадии, расходуются в последующей.

Обычно очень трудно рассчитать концентрацию промежуточного вещества в любое время. Аналитические выражения получены только для последовательных реакций с двумя односторонними мономолекулярными элементарными стадиями.

Это реакция типа:

Можно записать это в виде системы стадий:

закон скорости:

закон скорости :

где  скорости и константы скоростей первой и второй стадий реакции.

концентрации исходного вещества и концентрация промежуточного вещества. Это так называемые «текущие» концентрации, то есть концентрации в любой момент времени.

Решение прямой задачи кинетики

Для решения прямой задачи кинетики, то есть для нахождения зависимости концентрации от времени для любого участника реакции, предположим, что в предварительных опытах нам удалось найти константы скоростей каждой из стадий и мы точно знаем, что реакция описывается таким механизмом протекания.

Как обычно, чтобы найти в явном виде зависимость от времени нужно проинтегрировать дифференциальное кинетическое уравнение для первой стадии.

 дифференциальное кинетическое уравнение первой стадии;

 интегральное кинетическое уравнение первой стадии.

 уравнение кинетической кривой для исходного вещества.

Суммарная скорость образования промежуточного вещества равна алгебраической сумме скоростей образования вещества P в первой стадии и расходования его во второй стадии. Запишем это символами с учетом знаков

Для того, чтобы решить дифференциальное уравнение, преобразуем его следующим образом:

сгруппируем переменные, и умножим обе его части на величину (множитель Эйлера).

При этом нужно вспомнить, что в левой части

Теперь получим:

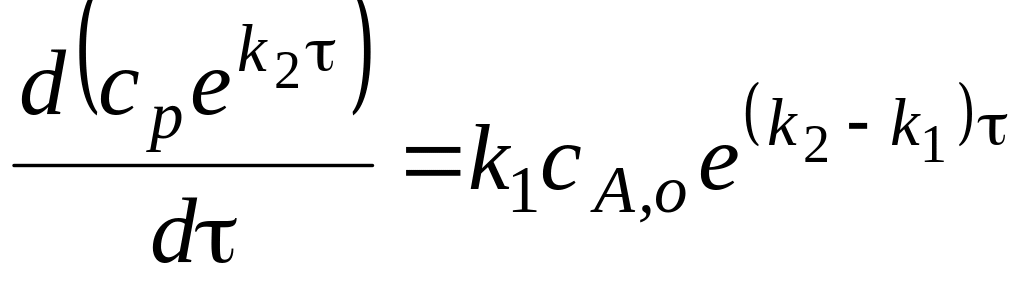
Интегрирование уравнения от 0 до и от 0 до приводит к выражению:

.

Теперь из уравнения легко выразить в явном виде зависимость концентрации промежуточного вещества от времени

.

Уравнение кинетической кривой для продукта последовательной реакции можно получить как интегрированием соответствующего дифференциального уравнения, так и по уравнению материального баланса, так как выражения кинетической кривой для исходного вещества и для промежуточного продукта мы только что вывели. Этот способ проще , им и воспользуемся:

В любой момент времени

Следовательно, легко получить:

Общий вид кинетических кривых представлен на рисунке

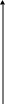
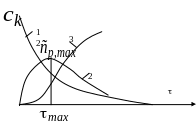
1 – зависимость концентрации исходного вещества от времени

2 – зависимость концентрации промежуточного вещества

3 – зависимость концентрации продукта последовательной реакции

Как видно из рисунка, на кинетической кривой промежуточного вещества имеется максимум, а на кинетической кривой продукта – вначале некоторый период с очень малой скоростью реакции- так называемый, индукционный период. В этот период идет в системе накопление промежуточного продукта, его еще мало и конечного продукта в системе почти нет. Легко видеть из расположения кривых, что максимум на кривой промежуточного продукта совпадает по времени с точкой перегиба на кривой конечного продукта. Кстати, кинетическая кривая такого вида, какой имеет кинетическая кривая конечного продукта, называется s-образной кривой. Часто такие кривые наблюдаются при автокаталитических реакциях.

Конечно, если мы говорим о максимумах и о точках перегиба, то имея, уравнения линий, мы легко найдем координаты максимума и координаты точки перегиба.

Например, найдем координаты максимума на кинетической кривой промежуточного продукта и проанализируем, от каких факторов зависят высота максимума и время достижения максимума.

Для этого нужно вспомнить, что в точке максимума первая производная уравнения кривой равна нулю.

Отсюда, можно получить выражение для времени максимума:

, где

Теперь можно найти и максимальную концентрацию промежуточного вещества.

Преобразуем показатели степени, учитывая, что

Анализируя полученные координаты максимума на кинетической кривой промежуточного вещества, можно сделать вывод, что высота максимума не зависит от абсолютных значений констант скоростей стадий, а зависит лишь от их соотношения. С ростом отношения , максимум на кривой смещается к началу координат и становится ниже.

Рассматривая решение прямой задачи, мы считали, что предварительно решили обратную. Она действительно, решается довольно просто.

Решение обратной задачи кинетики

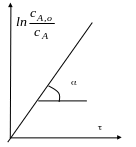
Константу скорости первой стадии

найдем линеаризацией экспериментальных данных по первой стадии

.

Величину константы скорости второй стадии найдем из соотношения

Анализ расположения кинетических кривых в зависимости от соотношения констант скоростей стадий

а) Если , то есть скорость превращения промежуточного вещества значительно выше скорости его возникновения, то

В этом случае можно говорить, что формально реакция протекает в одну стадию с константой скорости без образования промежуточного вещества

0

б) Если , то есть скорость образования промежуточного вещества значительно выше скорости его расходования, то

0

0.

То есть высота максимума на кривой промежуточного вещества не будет зависеть от значения констант.

В этом случае реакцию формально также можно представить как одностадийную, причем расход промежуточного вещества и образование конечного продукта будут характеризоваться константой скорости