Глава 4 случайные величины

В этой главе Вы сведете знакомство с новым и очень важ­ным понятием случайной величины.

Давайте вспомним вкратце содержание предыдущих глав. В первой главе Вы познакомились с простейшим спо­собом вычисления вероятности события — непосредствен­ным подсчетом доли благоприятных случаев. Только-только Вы освоились с этим способом, Вас постигло разочарова­ние: оказалось, что он применим далеко не всегда, а только в тех (сравнительно редких!) задачах, где опыт сводится к схеме случаев, т. е. обладает симметрией возможных ис­ходов. Зато в следующей главе Вы научились приближенно находить вероятность события по его частоте; на опыт ни­каких ограничений уже не накладывалось. Только-только Вы немножко освоились и с этим способом, как Вас опять постигло разочарование: оказалось, что не он является в теории вероятностей основным! В третьей главе («Основ­ные правила теории вероятностей») Вы, наконец-то, дошли до методов, которые, как следует из заглавия, являются в этой науке основными! «Наконец-то, — думаете Вы, — удалось мне добраться до самых основ, до самой сути! Боль­ше разочарований уже не будет!» Увы, Вас ждет еще одно (на этот раз последнее!) разочарование. Дело в том, что аппарат событий, с которым мы до сих пор имели дело, в современной теории вероятностей... не является основным!

— А какой же аппарат является основным? — кипя от негодования, спросите Вы. — И на кой черт Вы заставляли .меня знакомиться с не основным аппаратом?

— Беда в том, — смиренно ответим мы, — что без того, что Вы уже изучили, невозможно даже подступиться к сов­ременному аппарату.

— А что это за аппарат?

— Аппарат случайных величин.

Эта глава и будет посвящена основному понятию сов­ременной теории вероятностей — понятию «случайной ве­личины», разновидностям случайных величин, способам их описания и манипулирования с ними. О случайных вели­чинах мы будем говорить не так подробно, как о событиях, а более в «описательном» духе — здесь математический ап­парат, если бы мы им вздумали воспользоваться, оказался бы более сложным и мог бы оттолкнуть начинающего. А мы как раз хотим облегчить начинающему его «первые шаги». Итак, познакомимся с понятием случайной величины.

Случайной величиной называется величина, которая в результате опыта может принять то или другое значение, неизвестно заранее — какое именно.

Как всегда в теории вероятностей, определение «смут­новатое», содержит упоминание о какой-то неопределен­ности, неизвестности... Чтобы овладеть понятием случай­ной величины, надо к нему попросту привыкнуть. Для этого рассмотрим примеры случайных величин.

1. Опыт состоит в бросании двух монет. Число гербов, которое при этом появится, — случайная величина. Ее возможные значения: 0,1,2,3. Какое из них она примет — заранее неизвестно.

2. Ученик идет сдавать экзамен. Отметка, которую он получит, — случайная величина. Ее возможные значения: 2,3,4,5.

3. В группе студентов 28 человек. В какой-то день ре­гистрируется число неявившихся на занятия. Это — слу­чайная величина. Ее возможные значения: 0, 1, ..., 28.

— Ну, нет! — скажете Вы. — Все 28 человек никак заболеть (прогулять) не могут.

— Да, это практически невозможное событие. А кто Вам сказал, что все значения случайной величины должны быть одинаково вероятны?

Все приведенные в примерах случайные величины при­надлежат к типу так называемых дискретных. Дискретной называется такая случайная величина, возможные значе­ния которой отделены друг от друга какими-то интервала­ми. На оси абсцисс эти значения изобразятся отдельными точками.

Бывают случайные величины другого типа, которые на­зываются непрерывными. Значения таких случайных ве­личин сплошь заполняют какой-то участок числовой оси. Границы этого участка иногда бывают четкими, а иногда расплывчатыми, неопределенными. Рассмотрим несколько примеров непрерывных случайных величин.

1. Промежуток времени между двумя отказами («сбоя­ми») вычислительной машины. Значения этой случайной величины сплошь заполняют какой-то участок числовой оси. Нижняя граница этого участка вполне четкая - (0), а верхняя — расплывчатая, неопределенная, может быть найдена только в результате опыта.

2. Вес грузового поезда, подаваемого на станцию для разгрузки.

3. Высота подъема воды в половодье.

4. Ошибка, возникающая при взвешивании тела на аналитических весах (в отличие от предыдущих эта слу­чайная величина может принимать как положительные, так и отрицательные значения).

5. Удельный вес молока, берущегося на пробу в сов­хозе.

6. Время, проводимое учеником 8-го класса у телевизо­ра в течение дня.

Подчеркнем следующее: для того чтобы говорить о «слу­чайной величине» в том смысле, который приписывается этому понятию в теории вероятностей, необходимо уточ­нить, в чем состоит опыт, в результате которого случайная величина принимает то или другое значение? Например, в примере 1 непрерывной случайной величины надо указать, о какой машине идет речь, каковы ее возраст и условия экс­плуатации. В примере 4 надо уточнить, на каких весах про­изводится взвешивание? Какими разновесками? Необходи­мость уточнения условий опыта всегда надо иметь в виду, но, в целях краткости изложения, мы не всегда будем эти подробности оговаривать.

Обратим Ваше внимание на следующее обстоятельство. На самом деле все случайные величины, которые мы на­зывали «непрерывными», могут быть измерены только в каких-то единицах (минутах, сантиметрах, тоннах и т. д.) и в этом смысле, строго говоря, являются «дискретными». Например, случайную величину «рост человека» нет смысла измерять точнее, чем до 1 см; получается, в сущности, дис­кретная случайная величина со значениями, разделенными интервалом в 1 см. Но число таких значений очень вели­ко, и расположены они на оси абсцисс очень «тесно» — в таком случае удобнее рассматривать случайную величину как непрерывную.

Условимся в дальнейшем случайные величины обозна­чать большими буквами латинского алфавита, а их возмож­ные значения — соответствующими малыми (например, слу­чайная величина X, ее возможные значения x₁, х₂, ...), а самый термин «случайная величина» — иногда сокращать буквами СВ.

Итак, пусть перед нами СВ X с какими-то значениями. Естественно, что не все эти значения одинаково вероятны: среди них есть более и менее вероятные. Законом распределения случайной величины называется всякая функция, которая описывает распределение вероятностей между ее значениями. Мы познакомим Вас не со всеми формами законов распределения, а только с некоторыми, самыми простыми.

Закон распределения дискретной случайной величины может быть записан в виде так называемого ряда распре­деления. Так называется таблица, состоящая из двух строк: в верхней перечислены все возможные значения случайной величины: х₁, х₂, ..., х_п, а в нижней — соответствующие им вероятности : р₁, р₂, ..., р_п:

хi	х1	х2	……………	хn
pi	p1	p2	……………	pn

Каждая вероятность p_t есть не что иное, как вероятность события, состоящего в том, что СВ X примет значение х_i,:

P_i = P(X = х_i) (i = 1, ..., п).

Очевидно, сумма всех вероятностей p_i равна единице:

p₁₊ p_2+…..+ p_n=1

Эта единица как-то распределена между значениями СВ; отсюда и термин «распределение».

Пример 1. Производятся три независимых выстрела по мишени; вероятность попадания при каждом выстреле равна р =0,4. Дискретная СВ X — число попаданий в ми­шень. Построить ее ряд распределения.

Решение. Напишем в верхней строке ряда возмож­ные значения С В X: 0, 1, 2, 3, а в нижней — соответствующие им вероятности, которые обозначим р₀, р₁, р₂, p₃. Вычислять такие вероятности мы уже умеем (см. главу 3). Имеем:

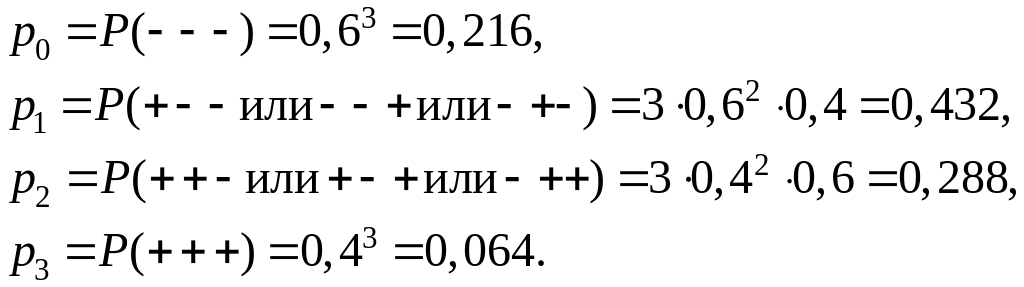
Проверим, равна ли сумма вероятностей единице: рав­на, значит, все в порядке. Ряд распределения СВ X имеет вид:

хi	0	1	2	3
pi	0,216	0,432	0,288	0,064

Пример 2. Спортсмен производит ряд попыток за­бросить мяч в кольцо. При каждой попытке (независимо от других) попадание в кольцо происходит с вероятностью р. Как только мяч попал в кольцо, попытки прекращаются. Дискретная СВ X — число попыток, которое придется про­извести. Построить ряд распределения СВ X.

Решение. Возможные значения СВ X : х₁= 1, х₂ = 2, ..., x_k = k, ... и т. д., теоретически — до беско­нечности. Найдем вероятности всех этих значений; р_i — это вероятность того, что мы попадем в кольцо при первой же попытке; она, очевидно, равна р: р_i = р. Найдем р₂ - вероятность того, что будут произведены две попытки. Для этого нужно совмещение двух событий:

1) при первой по­пытке мы не попадем в кольцо и

2) при второй — попадем.

Вероятность этого равна (1 — р)р. Аналогично находим р₃ = (1 — р)² р (первые две попытки не удались, а третья удалась), и вообще p_i = (1 — р)^i-1 р. Ряд распределе­ния СВ X имеет вид:

хi	1	2	3	…..	i	….
pi	p	(1 — р)р	(1 — р)2 р	…..	(1 — р)i-1 р	….

Заметим, что вероятности p_i образуют геометрическую прогрессию со знаменателем

(1 — р), поэтому такое рас­пределение вероятностей называется «геометрическим».

Теперь посмотрим, чем может характеризоваться рас­пределение вероятностей для непрерывной СВ. Для такой случайной величины, значения которой сплошь заполняют какой-то промежуток оси абсцисс, ряда распределения построить нельзя.

— Почему? — спросите Вы.

Отвечаем. Начнем с того, что нельзя записать даже верхнюю его строку, т. е. перечислить, одно за другим, все возможные значения СВ. Действительно, какую бы па­ру значений мы ни поставили рядом, между ними непремен­но найдутся еще значения *. Кроме того, на нашем пути встретится еще одна трудность: пытаясь приписать какую-то вероятность каждому отдельному значению непрерывной СВ, мы убедимся в том, что эта вероятность... равна нулю! Да, именно нулю — мы не обмолвились и постараемся Вас в этом убедить.

Вообразите себе, что перед нами целый пляж, усыпанный галькой. Нас интересует случайная величина X — вес отдельного камня.

Ну, что же — Давайте их взвешивать. Сначала начнем взвешивать с разумной точностью — до 1 г. Будем считать за 30 г вес всякого камня, который с точностью до 1 г равен 30 г. Получим какую-то частоту веса 30 г — какова она, мы сейчас не знаем, да это и неважно.

Теперь давайте усилим требования к точности — будем взвешивать камни с точностью до 0,1 г, т. е. считать ка­мень имеющим вес 30 г, если его вес с точностью до 0,1 г равен 30 г. При этом, очевидно, некоторые из камней, ко­торые мы при «грубом» взвешивании считали за тридцати­граммовые, отпадут. Частота события X = 30 (г), станет меньше. Во сколько раз? Примерно в 10.

А теперь еще повысим требования к точности — будем взвешивать камни с точностью до 1... мг! Частота появления веса 30 г станет еще в 100 раз меньше...

* Для лиц, знакомых с теорией множеств, прибавим: число этих значений несчетно.

А частота — родная сестра вероятности — прибли­жается к ней при большом числе опытов (камней на пляже много, так что в этом отношении мы можем быть спокойны— материал для взвешивания всегда найдется!). Какую же вероятность мы должны приписать событию, - состоящему в том, что вес камня будет ровно 30 г, ни на чуточку ни больше, ни меньше? Очевидно, нулевую - никуда не де­нешься !

Вы недоумеваете. Может быть, Вы даже возмущены! Вы ведь помните, что нулевой вероятностью обладают не­возможные события. А событие, состоящее в том, что не­прерывная СВ X примет какое-то значение х, возможно! Как же его вероятность может быть равна нулю?

Давайте вспомним хорошенько. Действительно, мы утверждали, что вероятность невозможного события равна нулю, и говорили совершенную правду. Но разве мы ут­верждали, что любое событие с нулевой вероятностью не­возможно? Нисколько! Теперь нам пришлось познакомить­ся с возможными событиями, вероятности которых равны нулю.

Не торопитесь. Давайте немного поразмышляем. За­будьте на минуту теорию вероятностей и просто вообразите себе на плоскости некоторую фигуру площади S. А теперь возьмем любую точку внутри фигуры. Чему равна площадь этой точки? Очевидно, нулю. Фигура, безусловно, состоит из точек; каждая из них обладает нулевой площадью, а вся фигура — ненулевой! Этот «парадокс» Вас уже не удив­ляет — просто Вы к нему уже привыкли. Вот так же надо привыкнуть и к тому, что вероятность попадания в каждую отдельную точку для непрерывной случайной величины в точности равна нулю *.

— Как же тогда можно говорить о распределении ве­роятностей для непрерывной случайной величины? — спросите Вы. — Ведь каждое из ее значений имеет одну и ту же вероятность: нуль!

Вы совершенно правы. О распределении вероятностей между отдельными значениями непрерывной СВ говорить не имеет смысла. А все-таки распределение и таких слу­чайных величин существует! Например, никому из Вас не придет в голову сомневаться, что значение роста человека 170 см вероятнее, чем 210 см, хотя и то, и другое значения возможны.

Тут нам придется ввести новое важное понятие: плот­ность вероятности.

Понятие «плотности» достаточно известно нам из фи­зики. Например, плотностью вещества называется его вес, приходящийся на единицу объема. А если вещество неод­нородно? Приходится рассматривать его местную плот­ность. Так же и в теории вероятностей мы будем рассмат­ривать местную плотность (т. е. вероятность, приходящуюся на единицу длины, в данной точке х).

* Следует оговориться, что бывают случайные величины особого, так называемого «смешанного», типа: кроме сплошного участка возмож­ных значений с нулевыми вероятностями, они имеют еще отдельные, особые значения с ненулевыми. Таких «хитрых» случайных величин мы с Вами рассматривать не будем, но знайте, что они существуют.

Плотностью вероятности непрерывной случайной ве­личины X называется предел отношения вероятности по­падания СВ X на малый участок, примыкающий к точке х, к длине этого участка, когда последняя стремится к нулю.

Понятие «плотности вероятности» легко выводится из родственного ему понятия «плотность частоты». Рассмотрим непрерывную СВ X (например, рост человека или вес камня на пляже). Давайте, прежде всего, произведем над этой слу­чайной величиной ряд опытов, в каждом из которых она принимает какое-то значение (например, измерим рост группы людей или же взвесим много камней). Нас интере­сует распределение вероятностей для нашей случайной ве­личины. Ну, что же, разобьем весь диапазон значений СВ X на какие-то участки (или, как говорят, «разряды»), например: 150—155 см, 155—160; 160—165,...., 190—195, 195—200. Подсчитаем, сколько значений СВ попало в каждый разряд*, разделим

.на общее число произведенных опытов — получим «частоту разряда» (очевидно, сумма частот всех разрядов должна быть равна единице). Теперь подсчитаем плотность частоты для каждого разряда, для чего раз­делим частоту на длину разряда (вообще говоря, длины раз­рядов не обязательно должны быть одинаковыми).

Если в нашем распоряжении достаточно большой массив статистических данных (порядка, скажем, нескольких сот, лучше — более), то, построив для нашей СВ плотность частоты, мы можем получить достаточное представление о распределении этой СВ — о ее плотности вероятности. При обработке такого статистического материала удобно, прежде всего, построить специальный

график, называемый гистограммой (рис. 2). Гистограмма строится следующим образом: на каждом разряде, как на основании, строится прямоугольник,

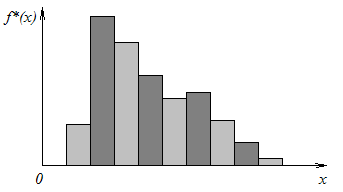
Рис. 2

площадь которого равна частоте разряда (а, значит, высота — плотности частоты). Очевидно, пло­щадь, ограниченная гистограммой, равна единице. По мере увеличения числа опытов N можно брать разряды все мень­шими и меньшими, при

этом «ступенчатый» характер ги­стограммы будет сглаживаться, и она будет приближаться к некоторой плавной кривой, которая называется кривой

* Если значение X попало в точности на границу двух разрядов, припишем по половине к каждому разряду

распределения (рис. 3).По оси ординат будет откладываться уже не плотность частоты, а плотность вероятности. Оче­видно, полная площадь, ограниченная кривой распределения, как и площадь ее «сестры» — гистограммы, — будет равна единице. А вероятность попадания

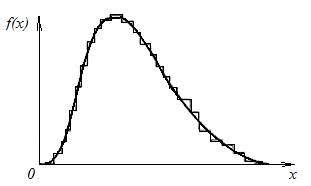
Рис. 3

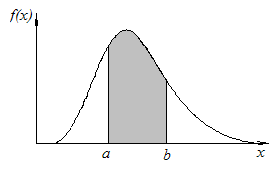
Рис. 4

СВ X на участок от а до b будет равна площади, опирающейся на этот учас­ток (рис. 4). Если обозначить плотность вероятности f(х), то вероятность попадания СВ X на участок от а до b вы­разится определенным интегралом:

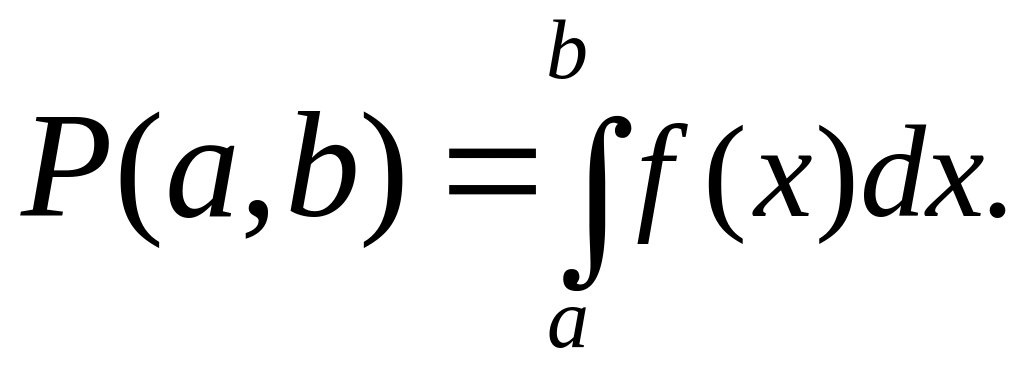
Таким образом, если не пожалеть времени и средств, интересующая нас плотность вероятности f(x) может быть определена как угодно точно по опытным данным. Но стоит ли овчинка выделки? Так ли уж нам нужно совершенно точно знать плотность f(x)? Очень часто нам этого не нужно: достаточно иметь лишь приближенное представление о законе распределения СВ X (ведь все вероятностные расчеты имеют по природе своей приближенный, «прикидочный» характер). А для того чтобы знать приближенно, «примерно», каков закон распределения СВ X, вовсе не нужно какого-то гран­диозного числа опытов, можно взять его довольно скромным, например 300—400, а иной раз и меньше. Построив гисто­грамму по имеющимся опытным данным, можно затем «вы­ровнять» ее с помощью той или другой плавной кривой (разумеется, такой, которая ограничивает площадь, равную единице). Теория вероятностей располагает целым набором кривых, удовлетворяющих этому условию. Некоторые из них обладают известными преимуществами перед другими, например, для них интеграл (1) легко вычисляется или для него оставлены таблицы. Или же условия возникно­вения нашей случайной величины подсказывают опреде­ленный тип распределения, вытекающий из теоретических соображений. Вдаваться здесь в такие подробности мы не будем — это дело специальное. Однако подчеркнем, что и при нахождении законов распределения случайных величин основное значение имеют не прямые, а косвенные методы, позволяющие находить распределения одних случайных величин не непосредственно из опыта, а через имеющиеся у нас данные о других случайных величинах, с ними свя­занных.

В осуществлении этих косвенных методов большую роль играет аппарат так называемых числовых характеристик случайных величин.

«Числовые характеристики» — это некоторые числа, характеризующие те или другие свойства, отличительные признаки случайных величин — например, среднее зна­чение, вокруг которого происходит случайный разброс, сте­пень этого разброса (как бы «степень случайности» случай­ной величины) и ряд других признаков. Оказывается, мно­гие задачи теории вероятностей можно решать, не прибегая (или почти не прибегая) к законам распределения, а поль­зуясь только числовыми характеристиками. Здесь мы по­знакомим Вас только с двумя (зато важнейшими!) числовы­ми характеристиками случайной величины: математи­ческим ожиданием и дисперсией.

Математическим ожиданием М [X] дискретной СВ X называется сумма произведений всех ее возможных зна­чений на соответствующие им вероятности:

М [X] = х₁р₁ + х₂р₂ + ... +х_пр_п, (1)

или короче, пользуясь знаком суммы:

(2)

где х₁, х₂, …, х_п — возможные значения СВ X, р_i — ве­роятность того, что СВ X примет значение x_i.

Как видно из формулы (2), математическое ожидание случайной величины X есть не что иное, как «среднее взве­шенное» всех ее возможных значений, причем каждое из них входит в сумму с «весом», равным его вероятности. Если число возможных значений СВ

(как в примере 2) бесконеч­но, то сумма (2) состоит из бесконечного числа слагаемых.

Математическое ожидание или среднее значение СВ является как бы ее «представителем», которым можно ее заменить при грубоориентировочных расчетах. В сущ­ности, мы так всегда и поступаем, когда в каких-нибудь задачах не учитываем случайности.

Пример 3. Найти математическое ожидание СВ X (число попаданий при трех выстрелах), рассмотренной в примере 1.

Решение. По формуле (2) имеем:

Для непрерывной СВ X тоже вводится понятие матема­тического ожидания, но, естественно, в формуле (2) сумма заменяется интегралом:

(3)

где f(х) — плотность вероятности непрерывной СВ X.

Теперь поговорим немного о математическом ожидании, о его физическом смысле и «генеалогии». Аналогично тому, как у вероятности есть «родная сестра» — частота, у мате­матического ожидания тоже есть родной брат (сестра? родственник?) — среднее арифметическое результатов на­блюдений. Так же как частота приближается к вероятности при большом числе опытов, так же с увеличением числа опытов среднее арифметическое наблюденных значений СВ приближается к ее математическому ожиданию.

Докажем это для дискретных СВ (думаем, что для не­прерывных Вы охотно примете это на веру!). Итак, пусть имеется дискретная СВ X с рядом распределения:

xi	x1	x2	…………..	xn
pi	p1	p2	…………	pn

Пусть произведено N опытов, в результате которых зна­чение х₁ появилось М₁ раз, значение х₂ — М ₂ раз и т. д. Найдем среднее арифметическое наблюденных значений СВ X; обозначим его :

Но есть не что иное, как частота события (X = х_i); обозначим ее

откуда

.

Мы знаем, что при увеличении числа опытов N частота события с практической достоверностью приближается к его вероятности p_i; значит, и среднее арифметическое наблюденных значений случайной величины при увеличении числа опытов с практической достоверностью будет сколь угодно близко к ее математическому ожиданию.

Подчеркнутое положение представляет собой одну из форм закона больших чисел (так называемую теорему Чебышева), играющую очень большую роль в практических при­ложениях теории вероятностей. Действительно, так же как неизвестную вероятность события можно приближенно определить по его частоте в длинной серии опытов, так же можно приближенно найти математическое ожидание СВ X как среднее арифметическое ее наблюденных значений:

(4)

Отметим специально, что для того чтобы вычислить по опытным данным математическое ожидание интересующей нас случайной величины, вовсе нет надобности знать ее закон распределения: просто надо вычислить среднее из всех результатов наблюдений.

Сделаем еще одно замечание: для того чтобы с удовлет­ворительной точностью найти математическое ожидание случайной величины, совсем не нужно столько опытов (порядка нескольких сот), как для построения гистограм­мы, а достаточно значительно меньшего числа (порядка десятков).

Теперь введем вторую важнейшую числовую характе­ристику случайной величины: ее дисперсию. Слово «дис­персия» в переводе значит «рассеивание» — дисперсия СВ характеризует как раз разброс (рассеивание) ее значений вокруг среднего. Чем больше дисперсия, тем «случайнее» случайная величина.

Дисперсия дискретной СВ X вычисляется так: из каж­дого возможного значения вычитается среднее (математи­ческое ожидание); полученное отклонение значения от среднего возводится в квадрат, множится на вероятность соответствующего значения, и все такие произведения суммируются; получается дисперсия, которую мы обозна­чим D[X ]:

или, короче,

(5)

Может возникнуть вопрос: а для чего нам понадоби­лось возводить отклонение от среднего в квадрат? Для то­го, чтобы избавиться от знака (плюс или минус). Разуме­ется, можно было бы от него избавиться, просто отбросив знак (взявши модуль отклонения), но получилась бы ха­рактеристика, гораздо менее удобная для вычисления и ма­нипулирования, чем дисперсия.

Пример 4. Найти дисперсию числа попаданий X в условиях примера 1.

Решение. По формуле (5) имеем:

Заметим, что формула (5) — не самая удобная для вы­числения дисперсии. Ее можно (и обычно удобно) вычис­лять по формуле:

(6)

т. е. дисперсия СВ равна математическому ожиданию ее квадрата минус квадрат математического ожидания.

Эту формулу легко вывести из (5) с помощью тождест­венных преобразований, но мы не будем на этом задержи­ваться. Лучше проверим ее справедливость на предыдущем примере:

.

Для непрерывных случайных величин дисперсия вы­числяется аналогично формуле (5), но, естественно, вместо суммы стоит интеграл:

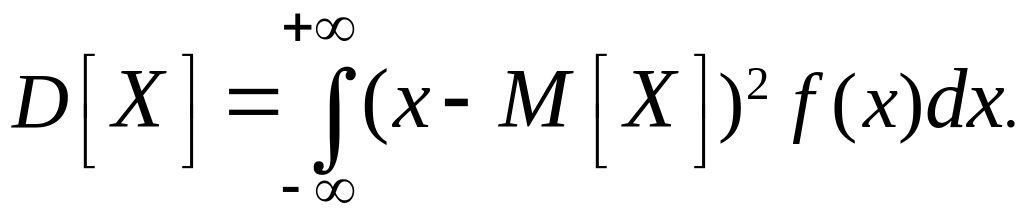(7)

Обычно удобнее бывает находить ее по формуле (6), которая для непрерывного случая даст:

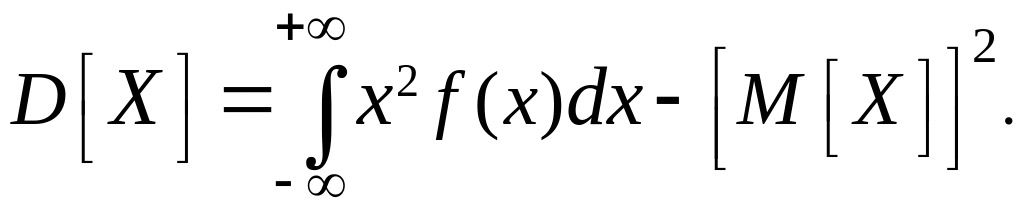(8)

Так же как для приближенного нахождения математи­ческого ожидания нет надобности в обязательном порядке знать закон распределения, так же можно приближенно найти и дисперсию непосредственно по результатам опы­тов, осредняя квадраты отклонений наблюденных значений СВ от их среднего арифметического:

(9)

где k — номер опыта; x_k — значение СВ, наблюденное в k-м опыте; N — число опытов.

Опять-таки удобнее вычислять дисперсию через «сред­ний квадрат минус квадрат среднего» по формуле:

(10)

Формулы (9) и (10) пригодны для грубоприближенной оценки дисперсии и при не очень большом числе опытов (лучше что-нибудь, чем ничего!) но, естественно, дают ее с не очень большой точностью. В математической статистике принято вводить в этом случае «поправку на малое число опытов», множа полученный результат на поправочный множитель . Разумеется, множить можно, но не нужно придавать этой поправке слишком большого значения, пом­ня о том, что при малом числе опытов все равно ничего хо­рошего из их обработки получить нельзя (как ни обрабаты­вай!), а при большом N поправоч-ный множитель близок к единице.

Дисперсия случайной величины как характеристика рассеивания имеет одну неприятную особенность: ее раз­мерность (как видно из формулы (5)) равна квадрату раз­мерности СВ X. Например, если СВ X выражается, скажем, в минутах, то ее дисперсия — в «квадратных минутах», что, согласитесь, не очень-то наглядно. Чтобы этого из­бежать, из дисперсии извлекают квадратный корень; по­лучается новая характеристика рассеивания — так на­зываемое «среднее квадратическое отклонение» (или, иначе, «стандарт»):

(11)

Среднее квадратическое отклонение — очень наглядная и удобная характеристика рассеивания. Она сразу же дает понятие о размахе колебаний СВ около среднего значения. Для большинства встречающихся на практике случайных величин с практической достоверностью можно утверждать, что они не отклонятся от своего математического ожидания больше чем на . Уровень доверия зависит от закона рас­пределения СВ, но во всех не искусственно придуманных случаях он довольно высок. Приведенное выше правило носит название «правила трех сигм».

Таким образом, если нам тем или другим способом удалось найти две числовые характеристики СВ X — ее математическое ожидание и среднее квадратическое от­клонение, мы сразу же получаем ориентировочное пред­ставление о том, в каких пределах могут лежать ее воз­можные значения.

Тут Вы можете спросить: если мы находили эти харак­теристики из опыта, кто нам мог бы помешать из того же опыта найти и пределы возможных значений?

Да, Вы совершенно правы, если эти характеристики на­ходятся непосредственно из опыта. Но не эти (прямые) методы нахождения числовых характеристик являются в теории вероятностей основными. Снова (уже в который раз!) мы скажем, что основными являются не прямые, а косвенные методы, позволяющие находить числовые ха­рактеристики интересующих нас случайных величин по числовым характеристикам других случайных величин, с ними связанных. При этом применяются основные правила действий с числовыми характеристиками; некоторые из них (разумеется, без доказательства) мы приведем здесь.

1. Правило сложения математических ожиданий: ма­тематическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых.

1. Правило сложения дисперсий: дисперсия суммы не­зависимых случайных величин равна сумме дисперсий сла­гаемых.

2. Правило вынесения неслучайного множителя из-под знака математического ожидания: неслучайную величину с можно выносить из-под знака математического ожидания, т. е. М [сХ] = сМ [X].

3. Правило вынесения неслучайного множителя из-под знака дисперсии: неслучайную величину с можно выносить из-под знака дисперсии, возводя ее в квадрат, т. е.

D [сХ] = с²D [X].

Все эти правила представляются довольно естествен­ными, кроме, может быть, последнего. Чтобы Вас убедить в его справедливости, возьмем такой пример. Пусть, ска­жем, мы удвоили случайную величину X. Ее математи­ческое ожидание, естественно, тоже удвоилось; отклонение отдельного значения от среднего тоже удвоилось, а квадрат этого отклонения учетверился!

Уже такого небольшого набора правил достаточно для того, чтобы решать некоторые интересные задачи, в чем Вы сейчас убедитесь.

Задача 1. Производится N независимых .опытов, в каждом из которых событие А появляется с вероятностью р. Рассматривается СВ X — число опытов, в которых появится событие А (короче, число появлений события А). Найти ма­тематическое ожидание и дисперсию случайной величины X.

Решение. Представим X в виде суммы N случайных величин:

(12)

где СВ X_k равна единице, если в k-м опыте событие А про­изошло, и нулю — если не произошло. Теперь применим к этому выражению правило сложения математических ожи­даний:

(13)

Так как опыты независимы, то случайные величины X_lt Х₂, ..., X_N также независимы. По правилу сложения дис­персий:

(14)

Теперь найдем математическое ожидание и дисперсию каждой из случайных величин X_k. Возьмем одну (любую) из них; это — дискретная СВ, имеющая два возможных значения: 0 и 1, с вероятностями (1 —р) и р. Математи­ческое ожидание такой СВ равно:

Дисперсию этой СВ найдем по формуле (6):

Подставляя в (13) и (14), получим решение задачи:

Задача 2. Производится N независимых опытов, в каждом из которых событие А происходит с вероятностью р. Рассматривается СВ Р* — частота события А в этой се­рии опытов. Найти приближенно диапазон практически возможных значений СВ Р*.

Решение. По определению частоты она равна числу X появлений события А, деленному на число опытов N:

Найдем числовые характеристики (математическое ожи­дание и дисперсию) этой случайной величины. Пользуясь правилами 3 и 4, получим:

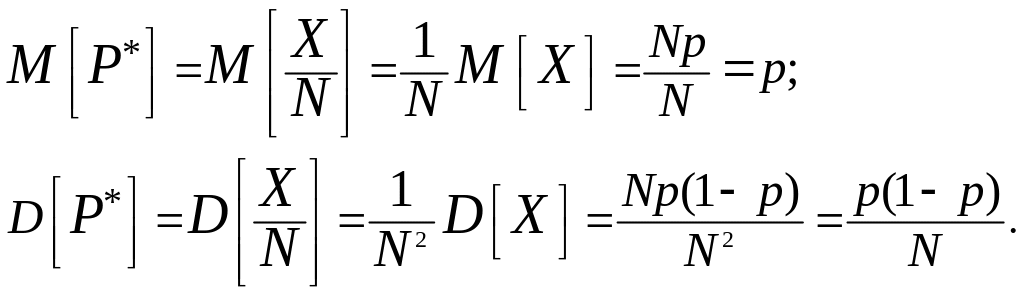
Извлекая корень квадратный из дисперсии, найдем среднее квадратическое отклонение :

А теперь воспользуемся «правилом трех сигм» и найдем приближенно диапазон практически возможных значений СВ Р*:

«Ба, да ведь это — наша старая знакомая! — вос­кликнете Вы, если были внимательны. — Ведь эту самую формулу нам демонстрировали для доверительного интер­вала, в который с вероятностью 0,997 уложится значение частоты события при большом числе опытов N. Наряду с ней (и даже предпочтительно) нам рекомендовали другую, где перед корнем стояла двойка, а не тройка, и та, помнит­ся, выполнялась с вероятностью 0,95. Формулы-то полу­чены. А вероятность откуда?»

Погодите, имейте терпение. Чтобы понять, откуда взя­лись вероятности 0,997 и 0,95, Вам нужно познакомиться с одним очень важным законом распределения — с так на­зываемым нормальным законом.

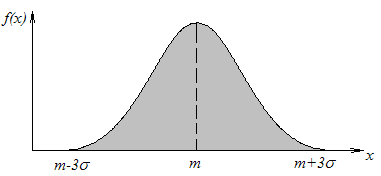
Рис. 5

Рассмотрим непрерывную случайную величину X. Го­ворят, что она «распределена по нормальному закону» (или «имеет нормальное распределение»), если ее плотность вероятности выражается формулой:

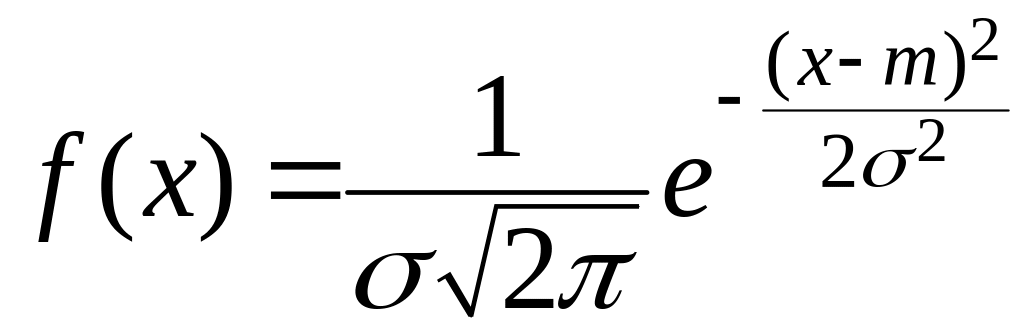(15)

где — известное Вам из геометрии число, а — так на­зываемое основание натуральных логарифмов ( 2,71828 ...). Кривая нормального закона имеет симмет­ричный, колоколообразный вид (рис. 5), достигая максиму­ма в точке т; по мере удаления от т плотность вероятности падает и в пределе стремится к нулю. Закон (15) зависит от двух параметров: и . Первый из них, т, как Вы, ве­роятно, догадались, есть не что иное, как математическое ожидание СВ X, а второй — — ее среднее квадратическое отклонение. При изменении т кривая f(х), не меняя своей формы, будет «ездить» туда-сюда вдоль оси абсцисс. Если же менять , кривая f(х) будет менять форму, стано­вясь при возрастании более «распластанной», а при умень­шении — более вытянутой вверх, «иглообразной».

Особая роль, которую играет нормальный закон в тео­рии вероятностей, связана с одним его замечательным свойством. Оказывается, если складывать большое число неза­висимых (или слабо зависимых) случайных величин, срав­нимых между собой по порядку своих дисперсий, то ка­ковы бы ни были законы распределения слагаемых, закон распределения суммы будет близок к нормальному — тем ближе, чем больше случайных величин складывается. При­веденное выше положение — это грубая формулировка так называемой «центральной предельной теоремы», играющей очень большую роль в теории вероятностей. У этой теоремы много различных форм, различающихся между собой условиями, которым должны удовлетворять случайные величины, чтобы их сумма с увеличением числа слагаемых «нормализовалась».

На практике очень многие случайные величины обра­зуются по «принципу суммы» и, значит, распределены нор­мально или почти нормально. Например, ошибки всевоз­можных измерений, представляющие собой сумму многих «элементарных», практически независимых, ошибок, выз­ванных отдельными причинами. По тому же закону распре­деляются, как правило, ошибки стрельбы, наведения, сов­мещения. Отклонения напряжения в сети от номинала так­же вызваны суммарным действием многих независимых причин, результаты действия которых складываются. Нор­мальному (или близкому к нему) закону подчиняются та­кие СВ, как суммарная выплата страхового общества за большой период, суммарное время простоя ЭЦВМ за год и т. д. Покажем, в частности, что такая интересная случай­ная величина, как частота события при большом числе опытов N, тоже имеет приближенно нормальное распре­деление. Действительно,

где X_k — случайная величина, равная единице, если в k-м опыте событие А появилось, и нулю, если не появилось. Отсюда видно, что частота Р* при большом числе опытов N есть сумма большого числа независимых слагаемых, при­чем каждое из них имеет одну и ту же дисперсию:

Отсюда заключаем, что частота Р* события А при боль­шом числе опытов N имеет приближенно нормальное рас­пределение.

Поскольку нормальный закон распределения часто встречается на практике, нередко приходится вычислять вероятность попадания СВ X, распределенной по нормаль­ному закону, в пределы участка (а, b). Интеграл (1) в этом случае не выражается через элементарные функции (как любят говорить студенты, «не берется»)- для его вычисления пользуются таблицами специальной функции — так назы­ваемой функции Лапласа:

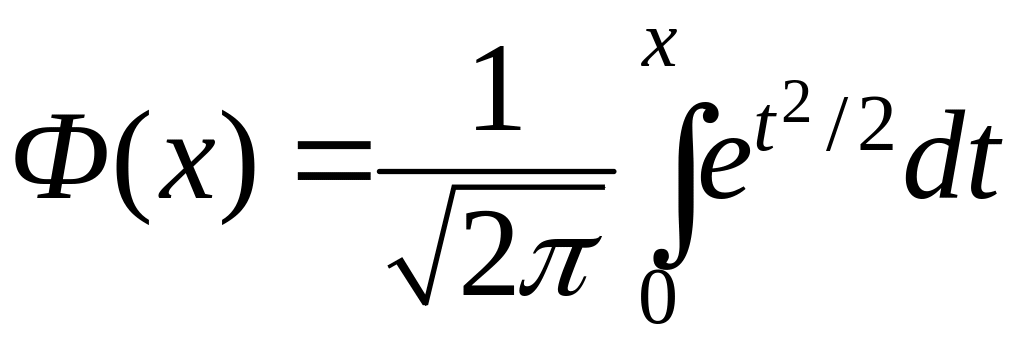
Краткие выдержки из таблиц функции Лапласа приведены в таблице

Таблица

x	Ф(х)	x	Ф(х)	x	Ф(Х)	x	Ф(х)
0,0	0,0000	1,0	0,3413	2,0	0,4772	3,0	0,4986
0,1	0,0398	1,1	0,3643	2,1	0,4821	3,1	0,4990
0,2	0,0793	1,2	0,3849	2,2	0,4861	3,2	0,4993
0,3	0,1179	1,3	0,4032	2,3	0,4893	3,3	0,4995
0,4	0,1554	1,4	0,4192	2,4	0,4918	3,4	0,4997
0,5	0,1915	1,5	0,4332	2,5	0,4938	3,5	0,4998
0,6	0,2257	1,6	0,4452	2,6	0,4953	3,6	0.4998
0,7	0,2580	1,7	0,4554	2,7	0.4965	3,7	0,4999
0,8	0,2881	1,8	0,4641	2,8	0,4947	3,8	0,4999
0,9	0,3159	1,9	0,4713	2,9	0,4981	3,9	0,5000

При можно принимать с точностью до 4 го знака после запятой Ф (х) = 0,5000.

При пользовании таблицей следует учитывать, что функ­ция Лапласа нечетная, т. е.

Ф (—х) = — Ф (х).

Вероятность попадания СВ X, имеющей нормальное рас­пределение с параметрами т и , в пределы участка (с, b) выражается через функцию Лапласа формулой:

(16)

Пример 5. Найти вероятность того, что СВ X, име­ющая нормальное распределение с параметрами :

а) отклонится от своего математического ожидания не боль­ше чем на 2 ; б) отклонится от него не больше чем на З .

Решение. Пользуясь формулой (16) и таблицей, найдем:

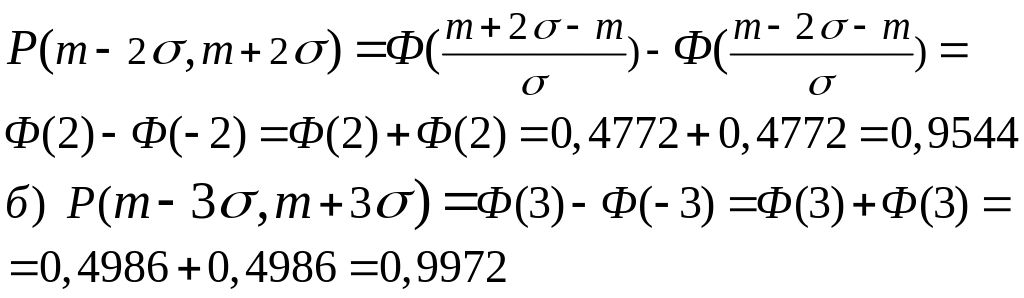
Так вот они, наконец, вычислены — две доверительные вероятности: 0,95 и 0,997, с которыми мы в главе 2 задавали доверительные интервалы для частоты события! Долгонько нам пришлось до них добираться...

Зато теперь, владея нормальным законом, мы можем решать некоторые поучительные задачи.

Пример 6. Поезд состоит из N = 100 вагонов. Вес каждого вагона—случайная величина с математическим ожи­данием m_q = 65 (т) и средним квадратическим отклонением _q = 9 (т). Локомотив может везти поезд, если его вес не превышает 6600 т; в противном случае приходится под­цеплять второй локомотив. Найти вероятность того, что этого делать не придется.

Решение. Вес поезда X можно представить как сум­му 100 случайных величин. Q_k — весов отдельных вагонов:

имеющих одно и то же математическое ожидание m_q = 65 и одну и ту же дисперсию D_q = ²_q = 81. По правилу сло­жения математических ожиданий:

М [X] = 100 • 65 = 6500.

По правилу сложения дисперсий:

D [X] = 100 • 81 = 8100.

Извлекая корень, найдем среднее квадратическое от­клонение: .

Для того, чтобы один локомотив мог везти поезд, нужно, чтобы вес поезда X оказался приемлемым, т. е. попал в пределы участка (0; 6600). Случайную величину X — сум­му 100 слагаемых можно считать распределенной нормально. По формуле (16):

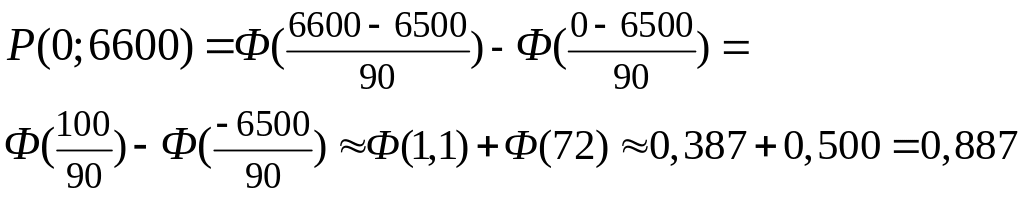
Итак, локомотив «справится» С поездом приблизительно с вероятностью 0,887.

Теперь давайте уменьшим число вагонов в поезде на два, т. е. возьмем N = 98. Подсчитайте сами вероятность того, что локомотив «справится» с поездом. Скорее всего результат подсчета Вас удивит: эта вероятность прибли­женно равна 0,99; значит, событие, о котором идет речь, практически достоверно! И всего-то для этого пришлось уб­рать два вагона...

Вот видите, какие любопытные задачки можно решать, имея дело с суммами большого числа случайных величин. Тут, естественно, возникает вопрос: а сколько это «мно­го»? Сколько нужно сложить случайных величин, чтобы закон распределения суммы уже «нормализовался»?

А это зависит от того, каковы законы распределения слагаемых. Бывают такие замысловатые законы, что нор­мализация наступает только при очень-очень большом числе слагаемых. Опять повторим: чего только не придумают математики! Но природа специально не устраивает нам та­ких пакостей. Обычно на практике для того, чтобы можно было пользоваться нормальным законом, бывает достаточ­но 5—6, ну 10, ну от силы 20 слагаемых (особенно если они имеют одно и то же распределение).

Быстроту, с которой «нормализуется» закон распре­деления суммы одинаково распределенных случайных ве­личин, можно проиллюстрировать на примере (тут Вам опять придется верить нам на слово — ничего не подела­ешь! Но до сих пор мы Вас не обманывали). Пусть имеется непрерывная СВ, распределенная с постоянной плотностью на участке (0; 1) (рис. 6). Кривая распределения имеет вид прямоугольника. Казалось бы, уж как непохоже на нормальный закон! А сложим две такие (независимые) случайные величины — получим новую СВ, распределен­ную по так называемому закону Симпсона (рис. 7). Тоже непохоже на нормальный закон, но уже лучше... А если сложить три такие равномерно распределенные случайные величины — получится СВ с плотностью, показанной на рис. 8, — кривая распределения состоит из трех отрезков парабол и по виду ужасно напоминает нормальный закон. А уж если сложить шесть равномерно распределенных слу­чайных величин — ни Вы, ни я, ни кто другой не сможет отличить кривую распределения от нормальной. На этом основан широко применяемый при моделировании случай­ных явлений на ЭЦВМ метод получения нормально распределенной случайной величины: достаточно сложить шесть независимых случайных величин, имеющих равномерное распределение на отрезке (0; 1) (кстати, датчиками таких случайных чисел оснащено в наше время большинство ЭЦВМ).

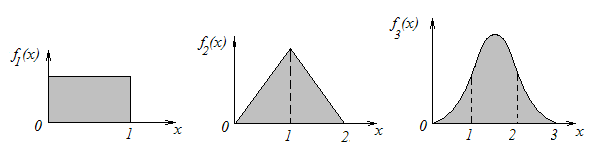
Рис. 6 Рис. 7 Рис. 8

И все-таки нельзя слишком увлекаться и сразу провоз­глашать нормальным закон распределения суммы нескольких случайных величин. Нужно сначала посмотреть (хотя бы в первом приближении), каковы их распределения. Если они, например, очень асимметричны, может понадобиться большое число слагаемых. В частности, нужно с некоторой осторожностью пользоваться правилом, что «при большом числе опытов частота события распределяется по нормаль­ному закону». Если вероятность события р в одном опыте очень мала (или, наоборот, очень близка к единице), для этого может понадобиться огромное число опытов. Кстати, сообщим Вам практический способ, позволяющий прове­рить, можно ли для частоты события пользоваться нор­мальным законом. Нужно по уже известному нам способу построить доверительный интервал для частоты события (с уровнем доверия 0,997):

и если он весь (оба его конца!) не выходит за разумные гра­ницы, в которых может лежать частота, и вероятность то­же (от 0 до 1), то можно пользоваться нормальным законом. Если же какая-нибудь из границ интервала оказывается за пределами отрезка (0, 1), то нормальным законом поль­зоваться нельзя. В таких случаях можно для приближенного решения задачи воспользоваться другим распределением — так называемым распределением Пуассона. Но разговор об этом распределении (так же, как и о ряде других, которых в теории вероятностей великое множество!) выходит за пределы наших «первых шагов».

В общем, в результате изучения нашей немудреного введения Вы, по-видимому, получили некоторое понятие о том, что такое теория вероятностей и чем она занимается. Возможно, что Вы получили к ней решительное отвраще­ние — в таком случае первое знакомство с ней станет для Вас и последним. Жалко, конечно, но ничего не поделаешь: есть люди (даже среди математиков!), органически не переносящие теории вероятностей.

Но возможно (для этого, в сущности, и написано введение), что тематика, методы и возможности теории вероятностей Вас заинтересовали. Тогда познакомьтесь с нашей наукой поподробнее (см. список литературы). Не будем скрывать, что углубленное знакомство с теорией вероят­ностей потребует от Вас умственных усилий, гораздо более серьезных, чем «первые шаги». Дальнейшие будут труднее, но зато и интереснее. Недаром говорит пословица: «корень учения горек, а плоды — сладки».