Глава 2 вероятность и частота

В предыдущей главе Вы познакомились с предметом теории вероятностей, с некоторыми ее основными понятия­ми (событие, вероятность события) и научились вычислять вероятности событий по так называемой «классической формуле»:

(1)

где п — общее число случаев, т_А — число случаев, бла­гоприятных событию А.

Однако из этого не следует, что Вы хорошо вооружены для применения теории вероятностей на практике. К сожа­лению, сфера применения классической формулы (1) не так обширна, как нам хотелось бы. Она пригодна только в тех опытах, которые обладают симметрией возможных исходов (сводятся к схеме случаев). А что это за опыты? Преимущественно относящиеся к области азартных игр, где симметрия обеспечивается специальными мерами. Так как в настоящее время профессия игрока не так уже рас­пространена (в давние времена это было иначе), практиче­ское значение формулы (1) для вычисления вероятностей очень ограниченно. Большинство опытов со случайным исходом, с которыми нам приходится иметь дело на прак­тике, не сводится к схеме случаев. Как же быть с вероят­ностями событий? Существуют ли они для таких опытов? А если существуют, как их вычислять?

Этим вопросом мы и займемся. Тут нам придется ввести в рассмотрение новое основное понятие теории вероятно­стей — понятие частоты события.

Будем подходить к нему несколько издалека. Предста­вим себе какой-то опыт, не сводящийся к схеме случаев, например бросание «неправильной», несимметричной иг­ральной кости ^*. Рассмотрим в этом опыте событие А — выпадение 6 очков. Так как опыт к схеме случаев не сво­дится, то формула (1) неприменима, и нельзя считать, что Р (А)=1/6. Чему же равна вероятность события А? Боль­ше она или меньше 1/6? И как ее найти хотя бы приближен­но? На такой вопрос легко ответит каждый разумный че­ловек. Он скажет: надо попробовать, побросать кость много раз подряд и посмотреть, насколько часто (в какой доле всех опытов) будет появляться событие А? Эту долю (или, в других терминах, «процент») появлений события А и можно принять за его вероятность.

^* Неправильность может быть достигнута, скажем, заделкой внутрь кости свинцового грузика, смещающего центр тяжести и увели­чивающего вероятность выпадения одних граней за счет других. Та­кого рода «фокусами», в целях обогащения, занимались в свое время профессиональные игроки в кости. Заметим, что предприятие было не­безопасным: игрока, у которого обнаруживалась фальшивая кость, нещадно избивали, а то и забивали насмерть.

А что? Наш «разумный человек», безусловно, прав! Сам того не зная, он воспользовался понятием «частоты события», которому мы сейчас и дадим точное определение.

Частотой события в серии из N опытов называется отношение числа опытов, в которых это событие произо­шло, к общему числу произведенных опытов.

Частоту события иначе называют его статистической вероятностью. Именно статистика массовых случайных явлений — база для определения вероятностей событий в опытах, не обладающих симметрией возможных исходов.

Условимся частоту события А обозначать Р*(А) (знак * ставится для того, чтобы отличить частоту от родственной ей вероятности Р (А). По определению

(2)

где N — общее число опытов, М_А — число опытов, в ко­торых появилось событие А (короче, число появлений события А).

Несмотря на внешнее сходство формул (1) и (2), они совершенно различны по существу. Формула (1) служит для теоретического вычисления вероятности события по заданным условиям опыта. Формула (2) служит для экспе­риментального определения частоты события; чтобы ею воспользоваться, необходим опытный, статистический ма­териал.

Давайте поразмышляем немного над природой частоты. Совершенно ясно, что между частотой события и его ве­роятностью существует некоторая

связь: более вероятные события, в общем, происходят чаще, чем маловероятные. Тем не менее понятия «частота» и «вероятность» отнюдь не тождественны. Сходство, «родство» между частотой и вероятностью проявляется тем заметнее, чем большее чис­ло опытов произведено. При малом числе опытов частота события в значительной мере случайна, может существен­но отличаться

от вероятности.

Например, при 10 бросани­ях монеты герб вполне может выпасть 3 раза, частота по­явления герба будет 0,3, что сильно отличается от вероят­ности 0,5. Однако при увеличении числа опытов частота события постепенно теряет свой случайный характер. Слу­чайные обстоятельства, сопровождающие каждый отдель­ный опыт, в массе опытов взаимно погашаются, и частота постепенно стабилизируется, приближаясь, с незначитель­ными колебаниями, к некоторой средней, постоянной ве­личине. Естественно предположить, что эта постоянная величина и есть не что иное, как вероятность события.

Разумеется, проверить это утверждение мы можем толь­ко для тех событий, вероятности которых могут быть вычислены по формуле (1), т. е. для опытов, сводящихся к схеме случаев. И что же? Утверждение оказывается правильным.

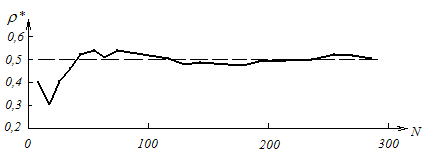
Рис. 1

Если не полениться, Вы можете сами его проверить на каком-нибудь простеньком примере. Проверьте, напри­мер, что при увеличении числа бросаний монеты частота появления герба будет приближаться к вероятности этого события 0,5. Бросьте монету 10, 20, ... раз (пока хватит терпения) и подсчитайте частоту появления герба в зави­симости от числа бросаний. Для экономии сил и времени можете применить «маленькую хитрость» — бросать моне­ты не по одной, а сразу десятками (разумеется, предвари­тельно встряхнув их хорошенько). Потом нанесите полу­ченные числа на график. У Вас получится нечто вроде зуб­чатой линии, изображенной на рис. 1. График рис. 1 по­лучен автором в результате 30-кратного бросания тщатель­но встряхнутого десятка копеечных монет. Может быть, у Вас хватит терпения произвести значительно большее число бросаний. Знайте, что в таких опытах Вы будете не одиноки: ими не брезговали и крупные ученые, интере­совавшиеся природой случайности. Например, знаменитый статистик К. Пирсон бросил монету 24 000 раз и получил при этом 12 012 гербов, что дает частоту, чрезвычайно близкую к 0,5. Неоднократно производились опыты и с бросанием игральной кости, и также давали частоты по­явления граней, близкие к 1/6. Таким образом, факт при­ближения частот к вероятностям можно считать эксперимен­тально проверенным.

Свойство устойчивости частот при большом числе од­нородных опытов — одна из наиболее характерных зако­номерностей, наблюдаемых в массовых случайных явлениях. Если мы повторяем (воспроизводим) один и тот же опыт много раз (причем обеспечена независимость исходов отдельных опытов), частота события становится все менее и менее случайной, выравнивается, приближается к постоянной. Для опытов, сводящихся к схеме случаев, мож­но непосредственно убедиться, что эта постоянная не что иное, как вероятность события. А если опыт к схеме слу­чаев не сводится, а частота обнаруживает устойчивость, приближается к постоянной? Ну, что же, примем, что правило остается в силе и назовем эту постоянную вероят­ностью события. Таким образом, мы ввели вероятности не только для событий и опытов, сводящихся к схеме случаев, но и для тех, которые к схеме случаев не сводятся, лишь бы в них наблюдалось свойство устойчивости частот.

Как же обстоит дело с устойчивостью частот? Все ли случайные явления эту устойчивость обнаруживают? Не все, но многие. Поясним эту далеко не простую мысль рас­суждениями. Постарайтесь хорошенько в них вникнуть: это избавит Вас от возможных ошибок в применении ве­роятностных методов.

Говоря выше об «устойчивости частот», мы предполага­ли, что можем неограниченное число раз повторять один и тот же опыт (бросание монеты, игральной кости и т. п.). Действительно, такой опыт ничто не мешает нам повторять сколько угодно раз — было бы время! А ведь бывает так, что «опыт» производим не мы сами, а только наблюдаем результаты тех «опытов», которые «ставит» за нас природа. В подобных случаях устойчивости частот заранее гаранти­ровать нельзя — в ней приходится каждый раз убеждаться.

Пускай, например, «опыт» состоит в рождении ребенка, и нас интересует вероятность события «рождение мальчика» («опытов» подобного рода природа ставит ежегодно огром­ное множество). Имеется ли в таких случайных явлениях устойчивость частот? Да, имеется. Экспериментально уста­новлено, что частота рождения мальчика очень устойчива, почти не зависит от географического положения страны, национальности родителей, их возраста и т. д. Эта частота несколько выше, чем 0,5 (приближенно равна 0,51)*. Свой­ством устойчивости частот (по крайней мере на не слиш­ком больших участках времени) обладают такие, например, случайные явления, как отказы технических устройств; брак на производстве; ошибки механизмов; заболеваемость и смертность населения; метеорологические, многие биоло­гические явления и т. д. Эта устойчивость и

позволяет с успехом применять вероятностные методы для изучения таких случайных явлений, для прогнозирования и управ­ления ими.

Наряду с этим существуют и такие случайные явления, для которых устойчивость частот сомнительна, а то и про­сто не существует. Это — такие явления, где бессмысленно говорить о большом количестве «однородных опытов», где не существует (или в принципе не может быть получен) достаточно обширный массив статистических данных. В подобных явлениях тоже могут наблюдаться те или другие события, вообще представляющиеся нам более или менее правдоподобными, но нет возможности приписать им какие-либо определенные вероятности. Например, вряд ли воз­можно (и вряд ли целесообразно!) вычислять вероятность того, что через три года женщины будут носить длинные юбки (или мужчины — длинные усы). Соответствующего массива статистических данных не существует; если рас­сматривать следующие друг за другом годы как «опыты», то их ни в каком смысле нельзя считать «однородными».

Другой пример, где еще менее осмысленно разговари­вать о вероятности события. Предположим, кто-то задался целью вычислить вероятность того, что на Марсе сущест­вует органическая жизнь. По-видимому, вопрос о том, существует она или нет, будет в ближайшие годы решен. Многие ученые считают наличие органической жизни на Марсе вполне правдоподобным. Но «степень правдоподо-

­

* При наличии некоторых особых условий (например, во время и после войны) эта частота по еще невыясненным причинам может откло­няться от многолетней устойчивой средней.

бия» еще не есть вероятность! Оценивая вероятность «на глаз», мы неизбежно оказываемся в мире туманных домыс­лов. Если мы хотим оперировать подлинными «вероятно­стями», мы должны опираться на достаточно обширную статистику. А можно ли говорить об обширном массиве статистических данных в этом случае? Разумеется, нет! Ведь Марс-то один!

Итак, уточним нашу позицию: о вероятностях событий в опытах, не сводящихся к схеме случаев, мы будем гово­рить только, если они относятся к категории массовых слу­чайных явлений, обладающих свойством устойчивости частот. Вопрос о том, обладают они им или нет, решается обычно на уровне здравого смысла. Можно ли достаточно много раз воспроизвести опыт, не меняя существенно его условий? Есть ли надежда собрать необходимую статистику? На эти вопросы должен ответить сам исследователь, собирающийся применить вероятностные методы в какой-то области.

Остановимся еще на одном вопросе, непосредственно связанном с предыдущим. Говоря о вероятности события в каком-то опыте, необходимо, прежде всего, тщательно оговорить основные условия опыта, которые предполага­ются фиксированными и не меняются при его повторении. Одна из самых частых ошибок в практическом применении теории вероятностей (особенно у начинающих) — это го­ворить о вероятности события, не уточняя условий опыта, о котором идет речь, и того «статистического массива» случайных явлений, в котором эта вероятность могла бы проявить себя в форме частоты.

Например, совершенно бессмысленно говорить о веро­ятности такого события, как «опоздание поезда». Сразу возникает ряд вопросов: Какого поезда? Откуда и куда он идет? Грузовой он или пассажирский? На какой железной дороге? и т. д. Только после уточнения всех этих подроб­ностей можно позволить себе рассматривать вероятность данного события как определенное число. Это мы преду­преждаем Вас о «подводных камнях», угрожающих тем, кто в теории вероятностей интересуется не только забав­ными задачками на «монеты», «кости» и «игральные карты», а хочет применять ее методы на практике, для достижения реальных целей.

Ну, а теперь предположим, что все эти условия выпол­нены: есть возможность произвести достаточно много одно­родных опытов, устойчивость частот — налицо. Тогда мож­но для приближенного определения вероятности события воспользоваться его частотой в длинной серии опытов. Ведь мы уже договорились, что при увеличении числа опы­тов частота события приближается к его вероятности. Как будто бы очень просто, а на деле — не очень. Соотношение между частотой и вероятностью довольно тонкое.

Поразмыслим немножко над термином «приближает­ся», который мы здесь употребили. Что это значит: «при­ближается»?

— Что за странный вопрос, — может быть, подумае­те Вы. — «Приближается» — значит становится все бли­же и ближе. О чем тут размышлять?

Нет, тут есть о чем размышлять. Ведь речь идет о слу­чайных явлениях, а в этих явлениях все по-особому, «не как у людей».

Когда мы говорим, что сумма членов геометрической прогрессии

при увеличении n стремится (неограниченно приближает­ся) к двум, это значит, что чем больше членов мы возьмем, тем ближе будет сумма к своему пределу, и это совершен­но достоверно. В области случайных явлений таких кате­горических утверждений делать нельзя. Да, частота собы­тия, вообще говоря, приближается к вероятности, но по-своему: не совсем наверняка, а почти наверняка, с очень большой вероятностью. Может оказаться, что частота со­бытия даже при очень большом числе опытов будет сильно отличаться от вероятности. Но вероятность этого очень мала, тем меньше, чем большее число опытов произведено.

Пусть, например, мы бросили монету N=100 раз. Спро­сим себя, может ли случиться, что частота появления герба будет сильно отличаться от вероятности Р (А)=0,5, на­пример, будет равна нулю? Для этого надо, чтобы герб не появился ни разу. Такое событие теоретически возможно (не противоречит законам природы), но вероятность его очень-очень мала. В самом деле, вычислим эту вероятность (к счастью, решать такие простые задачи мы уже умеем). Подсчитаем общее число случаев п. Каждая монета может выпасть двумя способами: гербом или решкой. Любой спо­соб выпадения каждой монеты может сочетаться с любым способом выпадения каждой из остальных. Отсюда общее число случаев 2¹⁰⁰. Благоприятен нашему событию (не­ появление ни одного герба) только один случай; значит, вероятность его равна 1/2¹⁰⁰. Это — величина чрезвычай­но малая, ее порядок — число с 30 нулями после запятой. Событие с такой вероятностью смело можно считать прак­тически невозможным. В действительности и гораздо мень­шие отклонения частоты от вероятности тоже будут прак­тически невозможными.

Какие же отклонения частоты от вероятности при боль­шом числе опытов практически возможны? Сейчас мы напи­шем формулу, позволяющую ответить на этот вопрос. До­казать эту формулу мы, к сожалению, не можем (некоторое обоснование ее будет дано в дальнейшем); пока что Вам остается только принять ее на веру *.

Пусть производится N опытов, в каждом из которых событие А появляется с вероятностью р. Тогда частота Р*(А) события А с вероятностью 0,95 укладывается на участок:

(3)

* Рассказывают, что знаменитый ученый Даламбер, обучая ка­кому-то разделу математики очень тупого и очень знатного ученика и не добившись понимания доказательства, в отчаянии воскликнул: «Ну, честное слово, сударь, эта теорема верна!». На что ученик отвечал: «Сударь, почему Вы мне сразу не сказали? Вы – дворянин и я – дворянин. Вашего слова для меня вполне достаточно!».

Участок, определяемый формулой (3), мы будем назы­вать «доверительным интервалом» для частоты события, соответствующим «уровню доверия» 0,95. Это значит, что наше предсказание, состоящее в том, что частота не вый­дет за пределы этого участка, будет выполняться почти всегда, точнее, в 95% всех случаев. Разумеется, в 5% слу­чаев мы будем ошибаться, но... «волков бояться — в лес не ходить». Другими словами, если бояться ошибок, то не надо браться за предсказания в области случайных яв­лений — все они осуществляются не «наверняка», а «почти наверняка».

Другое дело, что вероятность ошибки 0,05 может по­казаться кому-нибудь слишком высокой; тогда можно «перестраховаться» и построить немного более широкий доверительный интервал:

(4)

этому интервалу соответствует очень высокий уровень до­верия — 0,997.

Ну, а если потребовать полной достоверности предсказа­ния? Доверительной вероятности, равной единице? Тогда мы сможем только утверждать, что частота события не вый­дет за пределы участка от 0 до 1 — утверждение довольно тривиальное, которое было нам ясно и без всяких вычис­лений.

В предыдущей главе мы уже отмечали, что назначение той вероятности, при которой мы считаем событие прак­тически достоверным (т. е. уровня доверия), в какой-то мере всегда дело произвола. Давайте уговоримся в даль­нейших оценках точности определения вероятности по частоте довольствоваться скромным уровнем доверия 0,95 и пользоваться формулой (3). В конце концов, если мы иной раз и ошибемся, ничего катастрофического не произойдет.

Оценим по этой формуле практически возможный диа­пазон значений (доверительный интервал) для частоты появления герба при N=100 бросаниях монеты. Для нашего опыта p=0,5, 1 - p =0,5, и формула (3) дает:

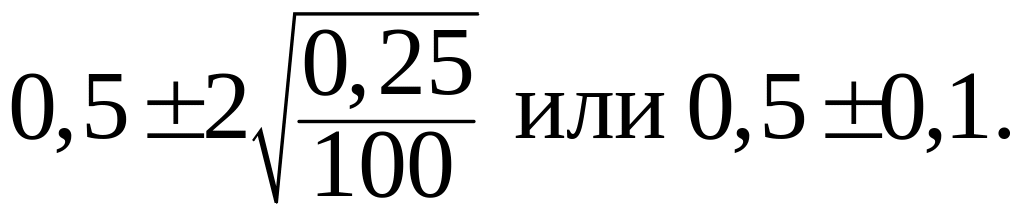
Таким образом, с вероятностью (уровнем доверия) 0,95 можно предсказать, что при ста бросаниях монет частота появления герба не отклонится от вероятности больше чем на 0,1. Гм... Ошибка, прямо сказать, не малая. Что де­лать, чтобы она была меньше? Очевидно, увеличить число опытов N. При увеличении N ширина доверительного ин­тервала уменьшается (к сожалению, не так быстро, как нам хотелось бы, а обратно пропорционально ). Напри­мер, при N=10 000 формула (3) даст 0,5±0,01.

Итак, связь между частотой и вероятностью события может быть сформулирована в следующем виде:

при достаточно большом числе независимых опытов частота события с практической достоверностью будет сколь угодно близка к его вероятности.

Это положение называется теоремой Я. Бернулли, а иначе «простейшей формой закона больших чисел». Мы здесь привели его без доказательства; однако вряд ли у Вас возникло серьезное сомнение в его справедливости...

Таким образом, мы разобрались в вопросе о том, что значит «частота приближается к вероятности». Осталось сделать еще один шаг: приближенно найти вероятность события по его частоте и оценить ошибку этого приближе­ния. В последнем нам поможет все та же формула (3), или, если хотите, (4).

Пусть мы произвели большое число опытов N, нашли частоту Р*(А) события А и хотим приближенно найти его вероятность. Обозначим кратко частоту Р*(А)=р*, а ве­роятность Р (А)=р и положим приближенно искомую вероятность равной частоте: (5)

А теперь оценим практически возможную максималь­ную ошибку приближенного равенства (5). Для этого вос­пользуемся формулой (3). Она нам покажет, насколько (с уровнем доверия 0,95) может отличаться частота от ве­роятности.

«А как же? — спросите Вы, — ведь в формулу (3) вхо­дит неизвестная нам вероятность р, а ее-то мы и хотим оп­ределить !»

Совершенно законный вопрос. Вы правы! Но дело в том, что формула (3) служит только для приближенной прикидки доверительного интервала. Для того чтобы грубо оценить ошибку в вероятности, можно в формуле (3) вме­сто неизвестной вероятности р поставить известную нам, приближенно равную ей, частоту р*.

Так и сделаем! Решим, например, такую задачу. В се­рии из N=400 опытов получено значение частоты события р* =0,25. Определить при уровне доверия 0,95, с какой максимальной практически возможной ошибкой мы найдем вероятность события, полагая ее равной частоте 0,25?

По формуле (3) с приближенной заменой р на р* =0,25 получим:

или приближенно 0,25±0,043.

Таким образом, максимальная практически возможная ошибка равна 0,043.

А как быть, если такая точность нас не устраивает? Если нам нужно знать вероятность точнее, с ошибкой, скажем, не больше 0,01? Разумеется, надо увеличить чис­ло опытов! Но до каких пор? Чтобы это узнать, восполь­зуемся снова нашей любимой формулой (3). Полагая в ней вероятность р приближенно равной частоте р*=0,25 в уже произведенной серии опытов, получим по формуле (3) приближенно максимальную практически возможную ошибку:

.

Положим ее равной заданному числу 0,01:

Решая это уравнение относительно N, получим: N=7500.

Итак, для вычисления по частоте вероятности порядка 0,25 с ошибкой не больше 0,01 (при уровне доверия 0,95) требуется произвести (страшно подумать!) 7500 опытов.

Формула (3) (или аналогичная ей (4)) может помочь при решении еще одного вопроса: можно ли объяснить по­лученное в опыте отклонение частоты от вероятности слу­чайными причинами или же оно показывает, что вероят­ность не такова, какой мы ее считаем?

Пусть, например, бросив монету N=800 раз, мы полу­чили частоту появления герба равной 0,52. У нас возникло подозрение, что монета «неправильная» и чаще выпадает гербом, чем решкой. Обосновано ли такое подозрение?

Чтобы ответить на этот вопрос, будем исходить из пред­положения, что все в порядке: монета правильная, ве­роятность выпадения герба нормальная, 0,5, и найдем до­верительный интервал (при уровне доверия 0,95) Для ча­стоты события «герб». Если полученное в опыте значение 0,52 укладывается в этот интервал — все в норме. Если нет - надо брать под подозрение «правильность» монеты. Формула (3) дает приближенно для частоты появления гер­ба интервал 0,5±0,035; полученное значение частоты укла­дывается в этот интервал, значит, придется «очистить» монету от подозрений в неправильности.

Аналогичными методами пользуются для того, чтобы судить: случайны или «значимы» различные отклонения от среднего, наблюдаемые в случайных явлениях (напри­мер, случайно был получен некоторый «недовес» в несколь­ких образцах расфасованных товаров, или же это указы­вает на систематический обман покупателя; случайно ли повысился процент выздоровлений у больных, применяв­ших данный препарат, или же это связано с применением препарата).

Таким образом, Вы научились по статистическим дан­ным приближенно находить вероятности событий в опытах, не сводящихся к схеме случаев, и даже как-то оценивать получающуюся при этом ошибку.

«Ну и наука эта теория вероятностей! — может быть, подумаете Вы. — Если вероятность события нельзя найти по формуле (1), приходится ставить опыты, и ставить, и ставить, пока хватит терпения и сил, потом подсчитать частоту события, положить ее равной вероятности и еще, может быть, оценить ошибку. Экая скучища!»

Подумаете, и будете совершенно неправы! Потому что такое «статистическое» нахождение вероятности — не един­ственный и далеко не главный прием. Гораздо большее значение в теории вероятностей имеют не прямые, а косвен­ные методы вычисления вероятностей. Они позволяют выражать вероятности интересующих нас событий через ве­роятности других событий, с ними связанных: вероятности сложных событий — через' вероятности простых. А те, в свою очередь, через вероятности еще более простых и т. д. Эта цепочка тянется до тех пор, пока мы не дойдем до самых простых, уже «неразложимых» событий; их вероят­ности либо вычисляются по формуле (1), либо находятся экспериментально, через частоты. Последнее, конечно, требует постановки опытов или сбора статистики; нужно стремиться к тому, чтобы цепочка событий была как можно длиннее, а необходимые опыты — как можно проще, дешевле. А для этого нужно как можно больше сведений по­лучить расчетным путем и как можно меньше — экспери­ментальным. Ведь из всех материалов, из которых делают­ся сведения, дешевле всего бумага и время ученого.

О том, как вычисляются вероятности сложных событий через вероятности простых, мы расскажем в следующей главе.