Решение типовых задач

Пример 1. В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответствен­но в 98%, 88 и 92% случаев.

Найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока.

Решение. Обозначим события:

A_i - телевизор поступил в торговую фирму от i-го постав­щика (i=1,2,3);

F - телевизор не потребует ремонта в течение гарантийного срока.

По условию

По формуле полной вероятности имеем

.

Пример 2. В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 се­мей 300 имеют холодильники.

Решение. Вероятность того, что семья имеет холодиль­ник, равна р = 80/100 = 0,8. Так как п = 100 достаточно велико

(условие выполнено), то применяем локальную формулу Муавра—Лапласа:

Вначале определим x: .

Отсюда имеем .

(значение ) найдено по табл. 2 приложений). Весьма малое значение вероятности не должно вызывать сомнения, так как кроме события «ровно 300 семей из 400 имеют холодильники» возможно еще 400 событий: «0 из 400», «1 из 400»,..., «400 из 400» со своими вероятностями. Все вместе эти события образуют полную группу, а значит сумма их вероятностей равна 1.

Пример 3. По данным примера 2 вычислить вероят­ность того, что от 300 до 360 (включительно) семей из 400 име­ют холодильники.

Решение. Применяем интегральную теорему Муавра— Лапласа ( ):

- функция

(или интеграл вероятностей) Лапласа, а

.

Таким образом:

Теперь, учитывая свойства Ф(х), получим

(по табл. II приложений Ф(2,50) = 0,9876, ).

Пример 4. По многолетним статистическим данным из­вестно, что вероятность рождения мальчика равна 0,515. Соста­вить закон распределения случайной величины X — числа маль­чиков в семье из 4 детей. Найти математическое ожидание и дисперсию этой случайной величины.

Решение. Число мальчиков в семье из п = 4 представля­ет случайную величину X с множеством значений X= т = 0, 1, 2, 3, 4, вероятности которых определяются по формуле Бернулли:

.

В нашем случае п=4, p=0,515, q=1 - p=0,485. Вычислим

(Здесь учтено, что ).

Ряд распределения имеет вид

X=m:

	0	1	2	3	4
	0,055	0,235	0,375	0,265	0,070

Убеждаемся, что .

Математическое ожидание М(Х) и дисперсию можно найти, как обычно, по известным формулам, но, в данном случае, учитывая, что закон распределения случайной величины Х биномиальный, можно воспользоваться простыми формулами

Пример 5. Функция задана в виде:

Найти:

а) значение постоянной А, при которой функция будет плотностью вероятности некоторой случайной величины X;

б) выражение функции распределения F(x);

в) вычислить веро­ятность того, что случайная величина X примет значение на от­резке [2;3];

г) найти математическое ожидание и дисперсию случайной величины X.

Решение.

а) Для того чтобы была плотностью ве­роятности некоторой случайной величины X, она должна быть неотрицательна, т.е. или , откуда

и она должна удовлетворять свойству 4 [Кремер]: {Вероятность попадания случайной величины в интервал [x₁,x₂) (включая х₁) равна приращению ее функции распределения на этом интервале, т.е. }. Поэтому в соответствии с формулой { } имеем

откуда А=3.

б) По формуле { } найдем F(x).

Таким образом,

в) По формуле { } имеем

.

Вероятность можно было найти непосредственно как приращение функции распределения по формуле { }:

.

г) По формуле { } вычислим

Дисперсию D(X) вычислим по формуле { }.

Вначале найдем

.

(вычисление интеграла аналогично приведенному выше). Теперь

.

Замечание. В ряде случаев, если имеется график функ­ции распределения F(x), полезно иметь в виду геометрическую интерпретацию математического ожидания М(Х) случайной ве­личины X:

где и - площади фигур, заключенных соответственно ме­жду осью Оу, прямой у=1 и кривой y=F(x) на интервале (0;+оо)

и между кривой y=F(x) и осями Ох и Оу на промежутке (рис. 4).

Рис. 4 Рис.5

Так, например, для нахождения математического ожидания М(Х) случайной величины X, заданной функцией распределения F(х), состоящей из участков прямых и дуги окружности [(рис. 5), нет необходимости находить по формуле, а затем М(Х) также по формуле. Значительно проще найти М(Х), используя его геометрическую интерпретацию, т. е.

.

Пример 6. При обследовании выработки 1000 рабочих

цеха в отчетном году по сравнению с предыдущим по схеме соб­ственно-случайной выборки было отобрано 100 рабочих. Полу­чены следующие данные (см. первые две графы табл. 1).

Необ­ходимо определить:

а) вероятность того, что средняя выработка рабочих цеха отличается от средней выборочной не более, чем на 1% (по абсолютной величине);

б) границы, в которых с веро­ятностью 0,9545 заключена средняя выработка рабочих цеха. Рассмотреть случаи повторной и бесповторной выборки.

Таблица 1

i	Выработка в отчетном году в про- центах к предыдущему x	Частота (количест- во рабо- чих)	Частость (доля рабочих)	Накоп- ленная частота	Накопленная частость
1	94,0-100,0	3	0,03	3	0,03
2	100,0-106,0	7	0,07	10	0,10
3	106,0—.112,0	11	0,11	21	0,21
4	112,0-118,0	20	0,20	41	0,41
5	118,0-124,0	28	0,28	69	0,69
6	124,0-130,0	19	0,19	88	0,88
7	130,0-136,0	10	0,10	98	0,98
8	136,0—142,0	2	0,02	100	1,00
		100	1,00	-	-

Решение.

а) Имеем N = 1000, n=100.

Вычислим упрощенным способом среднюю арифметическую и дисперсию распределения рабочих по выработке. Возьмем постоянную k, равную величине интервала, т.е. k=10, и постоянную с, равную середине пятого (одного из двух серединных) интервала, т.е. с=121. По формуле { } новые варианты .

Благодаря такому переходу получим вместо вариантов x_i=97,103,109,115,121,133 «простые» варианты u_i=-4,-3,-2,-1,0,1,2,3.

Теперь для расчета и по формулам { } необходимо найти суммы и .

Их вычисление представим в табл. 2.

Таблица 2

i	Интервалы х	Середина интервала xi
1	94,0- 100,0	97	-4	3	-12	48	-3	27
2	100,0- 106,0	103	-3	7	-21	63	-2	28
3	106,0- 112,0	109	-2	11	-22	44	-1	11
4	112,0- 118,0	115	-1	20	-20	20	0	0
5	118,0- 124,0	121	0	28	0	0	1	28
6	124,0- 130,0	127	1	19	19	19	2	76
7	130,0- 136,0	133	2	10	20	40	3	90
8	136,0- 142,0	139	3	2	6	18	4	32
			—	100	-30	252	—	292

В итоговой строке табл. 2 находим , .

Последний столбец – контрольный. Если таблица составлена верно, то

В данном случае , т.е. расчеты проведены верно.

Теперь по приведенным формулам

.

а) Найдем среднюю квадратическую ошибку выборки для средней:

для повторной выборки { } имеем

для бесповторной выборки { }

Теперь искомую доверительную вероятность находим по формуле :

(Значения Ф(t) находим по табл. II приложений).

Итак, вероятность того, что выборочная средняя отличается от генеральной средней не более чем на 1 % (по абсолютной ве­личине), равна 0,715 для повторной и 0,741 для бесповторной выборки.

б) Найдем предельные ошибки повторной и бесповторной выборок по формуле { }, в которой t = 2,00 (находим по табл. II приложений при данной в условии доверительной вероятно­сти у из соотношения = Ф(t) = 0,9545 ).

= 1,870(%).

= 1,774(%).

Теперь искомый доверительный интервал определяем по { }:

Таким образом, с надежностью 0,9545 средняя выработка ра­бочих цеха заключена в границах от 117,33 до 121,07%, если вы­борка повторная, и от 117,43 до 120,97%, если выборка бесповторная.

Пример 7. Для эмпирического распределения рабочих цеха по выработке по данным первых двух граф табл.1 примера 6 подоб­рать соответствующее теоретическое распределение и на уровне значимости = 0,05 проверить гипотезу о согласованности двух распределений с помощью критерия .

Решение. По виду гистограммы распределения рабочих по выработке (рис. 1) можно предположить нормальный за­кон распределения признака. Параметры

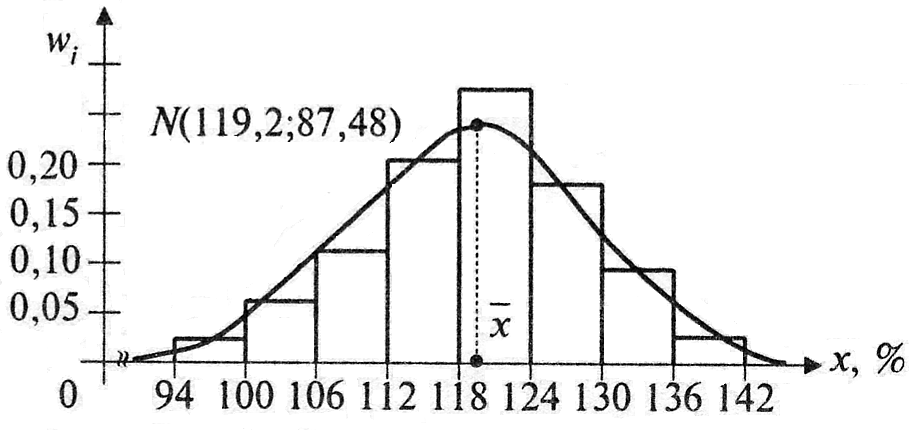
Рис.1

нормального закона а и ², являющие­ся соответственно математическим ожиданием и дисперсией случайной величины X, неизвестны, поэтому заменяем их «наилучши­ми» оценками по выборке — не­смещенными и состоятельными оценками соответственно выбо­рочной средней и «исправленной» выборочной дисперсией . Так как число наблюдений n=100 достаточно велико, то вме­сто «исправленной» можно взять «обычную» выборочную дис­персию s². В примере 6 вычислены .

Для расчета вероятностей , попадания случайной величин Х в интервал [x_i,,x_i+I] используем функцию Лапласа в соответст­вии со свойством нормального распределения:

Например,

и соот­ветствующая первому интервалу теоретическая частота и т.д.

Для определения статистики удобно составить таблицу:

Таблица

i	Интервал [xi,xi+1]	Эмпири- ческие Частоты	Вероят- ности	Теорети- ческие Частоты
1	94-100		0,017
					5,76	0,758
2	100-106		0,059
3	106-112	11	0,141	14,1	9,61	0,682
4	112-118	20	0,228	22,8	7,84	0,344
5	118-124	28	0,247	24,7	10,89	0,441
6	124-130	19	0,182	18,2	0,64	0,035
7	130-136		0,087
					0,16	0,014
8	136-142		0,029
		100	0,990	99,0	-

Учитывая, что в рассматриваемом эмпирическом распреде­лении частоты первого и последнего интервалов (n₁=3, n₈=2 ) меньше 5, при использовании критерия -Пирсона в соответ­ствии с замечанием {Замечание: Статистика

имеет - распределение лишь при , поэтому необходимо, чтобы в каждом интервале было достаточно наблюдений, по крайней мере, 5 наблюдений. Если в каком – нибудь интервале число наблюдений , имеет смысл объединить соседние интервалы, чтобы в объединенных интервалах было меньше 5*} целесообразно объединить указан­ные интервалы с соседними (см. табл.).

Итак, фактически наблюдаемое значение статистики =2,27.

Так как новое число интервалов (с учетом объединения крайних) т=6, а нормальный закон распределения определяется r = 2 параметрами, то число степеней свободы k=m-r-1= 6-2-1 = 3. Соответствующее критическое значение статистики по табл. III приложений . Так как , то гипотеза о выбранном теоретическом нормальном законе с параметрами

N(119,2; 87,48) согласуется с опытными данными.

Пример 8. Дана зависимость между суточной выработкой продукции Y(т) и величиной основных производст­венных фондов X (млн руб.) для совокупности 50 однотипных предприятий (табл.1).

Таблица 1

Величина ОПФ,млн. руб. (Х)	Середины интервалов	Суточная выработка продукции, т(Y)					Всего ni	Групповая средняя, т
		7-11	11-15	15-19	19-23	23-27
	yj xi
20-25	22,5	2	1	-	-	-	3	10,3
25-30	27,7	3	6	4	-	-	13	13,3
30-35	32,5	-	3	11	7	-	21	17,8
35-40	37,5	-	1	2	6	2	11	20,3
40-45	42,5	-	-	-	1	1	2	23,0
Всего nj		5	11	17	14	3	50	-
Групповая средняя , млн. руб.		25,5	29,3	31,9	35,4	39,2	-	-

(В таблице через и обозначены середины соответствую­щих интервалов, а ,- и — соответственно их частоты).

Найти: 1)вычислить групповые средние и и построить эмпирические линии регрессии; 2) предполагая, что между переменными X и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессий и построить их на одном чертеже с эмпирическими линиями регрессии; б) вычислить коэффициент

* Поэтому при вычислении числа степеней свободы в качестве величины т берется соответственно уменьшенное число интервалов.

корреляции, на уровне =0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;

в) используя соответствующее уравнение регрессии оценить среднемесячную выработку продукции, если величина ОПФ составляет 42 млн. руб.

Решение.

1) Изобразим полученную зависимость графически точками ко­ординатной плоскости (рис.1). Такое изображение статисти­ческой зависимости называется полем корреляции.

Для каждого значения x_i(i - 1,2,...,l), т.е. для каждой строки корреляционной таблицы вычислим групповые средние

где — частоты пар ( ) и ; m - число интервалов по

переменной Y.

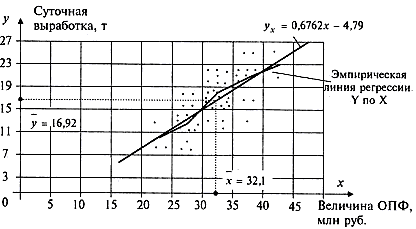
Рис. 1

Вычисленные групповые средние , поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X (рис.1).

Аналогично для каждого значения y_j (j = 1,2,...,т) по формуле

вычислим групповые средние (см. нижнюю строку корреляционной таблицы), где , l- число интервалов по переменной Х.

2.а) Найдем уравнения рег­рессии Y по X и X по Y и поясним их смысл.

Вычислим все необходимые суммы:

(обходим все заполненные клетки корреляционной таблицы).

Затем по формулам (12.12)—(12.22) [Кремер] находим выборочные ха­рактеристики и параметры уравнений регрессии:

Итак, уравнения регрессии

Из первого уравнения регрессии Y по X (его график показан на рис.1) следует, что при увеличении основных производст­венных фондов (ОПФ) X на 1 млн. руб. суточная выработка про­дукции Y предприятия увеличивается в среднем на 0,6762 т. Вто­рое уравнение регрессии X по Y показывает, что для увеличения суточной выработки продукции Y на 1т необходимо в среднем увеличить ОПФ X на 0,8099 млн. руб. (отметим, что свободные члены в уравнениях регрессии не имеют реального смысла).

2.б) Вычислим коэффициент корреляции между величиной основных производственных фондов X и суточной выработкой продукции Y (по данным табл.1

Выше мы получили

По формуле { } имеем (берем радикал со знаком +, так как коэффициенты и положительны). Итак, связь между рассматриваемыми пе­ременными прямая и достаточно тесная (ибо r-близок к 1): {Свойство коэффициента корреляции

.

В зависимости от того, насколько |r| приближается к 1, различают связь слабую, умеренную, заметную, достаточно тесную и весьма тесную, т.е., чем ближе |r| к 1, тем теснее связь}

Проверить теперь значимость коэффициента корре­ляции между переменными Х и Y.

Статисти­ка критерия по { } равна

.

Для уровня значимости = 0,05 и числа степеней свободы k = 50 — 2 = 48 находим критическое значение статистики (см. табл. IV приложений). Поскольку коэффи­циент корреляции между суточной выработкой продукции Y и величиной основных производственных фондов X-значимо отли­чается от нуля, а это, в свою очередь, означает наличие линейной корреляционной связи и, судя по величине r, достаточно тесной связи.

2.в) Найдем среднемесячную выработку продукции при величине ОПФ в 42 млн. руб. Подставляя в уравнение регрессии Y по Х , 42 млн. руб., получим

.