2.2.1. Определение критической глубины
Для прямоугольного сечения (m=0) можно воспользоваться следующей формулой:
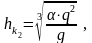(2.31)
где –
удельный расход, м2/c , b – ширина
лотка быстротока, принятая равной ширине
понизу в подводящем канале, α – коэффициент
Кориолиса (α =1,1).
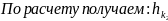=0,98
м.
2.2.2. Определение критического уклона
Для определения критического уклона использую следующие формулы:
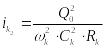(2.32)
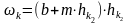(2.33)
По расчету получаем
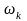=1.96
м2
(2.34)
(2.35)
По расчетам получаем
=3,96 м и
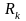=0,49 м, y
= 0,204 т.к. R<1,
n =
(2.36)
По расчету получаем:
=
46,48
,
=
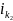0,0042 .
Сравнивая , с заданным можно сделать вывод, что поток находится в бурном состоянии.
2.2.3. Определение нормальной глубины
Определим нормальную глубину ,используя графоаналитический метод.
а) определяем необходимую расходную характеристику, соответствующую нормальной глубине , вычисляя:
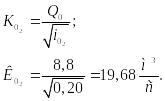(2.37)
По расчету получаем:
13,3
.
б) вычисляем расходные характеристики.
Примечание: y=
= 0,204, n = n
a= 1,33·0,014=
0,0186.
в) строим кривую К = f(h) . Приложение 6 (рис. 8).
Расчет расходных характеристик сведем в таблицу 7:
Таблица 7
-
Расчетные формулы
Ед. изм.
Назначаемые и определяемые величины
h1
h2
h3
h4
h5
h
м
0,2
0,4
0,6
0,8
1
м2
0,4
0,8
1,2
1,6
2
м
2,4
2,8
3,2
3,6
4
м
0,17
0,29
0,38
0,44
0,5
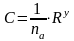
м0,5/с
37,30
41,64
44,01
45,57
46,67
м2/с
6,09
17,81
32,34
48,60
66,01
Из графика видно, что при значении
=13,3
,
принимает значение равное: 0,32 м.
2.2.4. Расчет кривой свободной поверхности на быстротоке
Исследуя дифференциальное уравнение неравномерного движения в призматических руслах
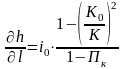(2.38)
где Пк – параметр кинетичности, сделаем вывод о типе и форме кривой свободной поверхности на быстротоке.
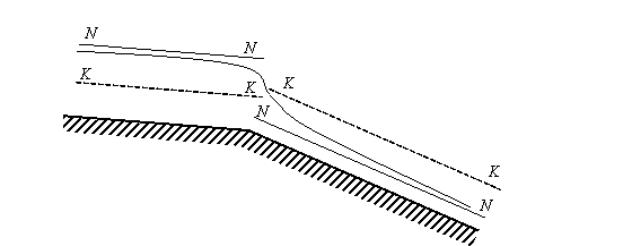
Рис.9. Схема
распределения глубин(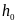
и
)
на участках с
уклоном
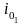и
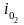
По схеме (рис. 9) принимаем глубину на
изломе
.
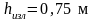Существует несколько методов расчёта кривой свободной поверхности на водоскате быстротока: Б.А. Бахметева, метод академика Н.Н. Павловского и другие. В практике дорожно-мостового и аэродромного строительства приходится решать задачи по расчёту неравномерного плавноизменяющегося движения воды не только в призматических руслах, но и на непризматических участках каналов. Поэтому используется универсальный метод конечных разностей В.И. Чарномского.
Метод В.И. Чарномского заключается в
следующем: зная глубину в одном из
сечений канала, например глубину на
изломе дна подводящего канала и лотка
быстротока hn = hизл,
задаёмся значением глубины в соседнем
сечении
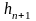и находим искомое расстояние Δl между
двумя соседними сечениями с известными
глубинами по уравнению[1]:
(2.39)
где ΔЭ – изменение удельной энергии сечения в пределах выбранного участка; iтр - уклон трения (среднее значение гидравлического уклона в пределах рассматриваемого участка).
Приведем необходимые для расчета понятия и формулы с нумерацией по столбам:
1)
;
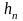- последняя глубина на быстротоке
принимается на 5% больше нормальной
глубины, т.е.
;
промежуточные глубины рекомендуется
задавать с интервалом 0.1 м, опираясь на
удобные при последующем построении
числовые значения глубин.
2)
,
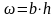т.к. лоток прямоугольной формы и
коэффициент откоса m = 0;
3)
,
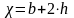т.к. лоток прямоугольной формы и
коэффициент откоса m = 0;
4) , т.к. лоток прямоугольной формы и коэффициент откоса m = 0;
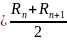
5)
, (2.40)
где
- гидравлические радиусы, соответствующие
соседним глубинам;
6)
,
где na – коэффициент шероховатости
с учётом аэрации потока;
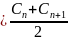
7)
, (2.41)
где
- коэффициенты Шези, соответствующие
соседним глубинам;
8)
,
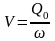где
- заданный расход воды, поступающий из
подводящего канала;
9)
, (2.42)
где
- средние скорости в соседних сечениях;
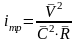
10)
; (2.43)т
11)
.к. лоток прямоугольной формы и m = 0;
,
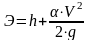(2.44)
где Э – удельная энергия соответствующих сечений;
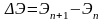
12)
, (2.45)
где
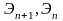- удельные энергии соседних сечений,
причём в последующем сечении для данного
типа кривой спада удельная энергия
сечения больше, чем в предыдущем;
13)
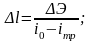
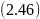
14) l1 =0, т.к. расчёт кривой
свободной поверхности начинается с
точки излома дна; последующее числовые
значение длин l2 , l3, определяются
путём наращивания, а именно:
,
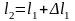и т.д. Для удобства расчет сведем в
таблицу 8:
Таблица 8
-
h
ω
χ
R
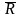
C
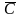
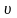
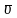
Э
∆Э
∆l
l
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0,65
1,3
3,3
0,39
44,62
4,46
1,77
0
0,39
44,52
4,55
0,03
0,07
0,40
0,625
1,25
3,3
0,38
44,41
4,64
1,83
0,41
0,38
44,30
4,74
0,03
0,08
0,49
0,6
1,2
3,2
0,38
44,19
4,83
1,91
0,89
0,35
43,67
5,32
0,04
0,48
3,25
0,5
1
3
0,33
43,16
5,8
2,39
4,11
0,31
42,50
6,53
0,08
0,96
8,44
0,4
0,8
2,8
0,29
41,85
7,25
3,35
12,55
0,27
41,32
7,94
0,14
1,17
22,2
0,336
0,67
2,7
0,25
40,79
8,63
4,51
34,74
2.2.5. Построение кривой свободной поверхности на водоскате
Быстротока
По полученным данным (табл. 8), построим кривую свободной поверхности на водоскате быстротока и определим по ней величину hкб , глубину на конце быстротока. Приложение 7(рис. 10).