МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
Индивидуальное задание №3 По курсу «Методы оптимизации» Вариант №27
Выполнил:
студент факультета математики и
информационных технологий
группы 3-З «КТ»
Баранов Даниил
Донецк 2013
Задача 1.В
приведенной далее таблице 4
для каждого варианта указаны значения
параметров целевой функции задачи
нелинейного программирования (ЗНП) и
координаты вершин
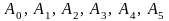выпуклого многоугольника, задающего
множество допустимых точек ЗНП, причем
целевая
функция задана в виде
,
,
,
,
а ЗНП поставлена на максимум.
Выполнить следующие задания:
восстановить математическую модель ЗНП, воспользовавшись данными Таблицы 4;
выполнить две итерации методом линеаризации, взяв в качестве начальной точку
.
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
27 |
-8 |
5 |
5 |
-11 |
4 |
10 |
-6 |
0 |
0 |
0 |
8 |
8 |
7 |
2 |
12 |
5 |
10 |
8 |
0 |
Восстановим заданную квадратичную функцию по формуле:
,
,
,
,
ЗНП поставлена на максимум.
=(4,10)*
=
=
*
=
=
*
=
f(x)=
-4
Найдем ограничения:
4
3
max( -4 )
(1)
Поставленная в (1) задача, является задачей нелинейного программирования с линейными ограничениями.
1. Строим область М.
Выберем:
,
Проверим:
.
Для этого введем вспомогательную функцию
:
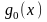,х-
;
=
f
′(
)
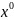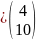.Тогда
.
Проверим условие:
.Т.е.: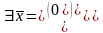
2. Составим вспомогательную задачу линейного программирования.
max
т.
.
Тогда
.
Строим
направление
,
где
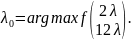
Замена
.
′(
+128
+128=0
Тогда
Проверим:
.
Для этого введем вспомогательную функцию
:
,х-
;
=
)=
.
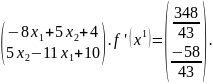
Проверим
условие:
Т.е.
.
3.Составим вспомогательную задачу линейного программирования.
max
Решаем графическим методом.
т.
.
Тогда
.
Строим
направление
,
Замена
.
+
-
′(
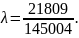
Проверим:
.
Для этого введем вспомогательную функцию
:
=
Проверим
условие:
.Т.е.:
.
Значит,
не является решением задачи (1).
Задача 2. Для поставленной в п. 1 задачи 2 ЗНП проверить крайние точки множества допустимых точек на оптимальность, воспользовавшись теоремой Куна-Таккера.
Строим область С:
1)Приведем задачу к нужному виду :
max(-4
)
2)Проверяем вогнутость f:
-
вогнуты,
так как линейны.
3) Из графика области С, следует, что С– выпуклое множество.
4)Проверяем условие регулярности Слейтера:
5)Составим функцию Лагранжа :
L(x,
6)Составим систему для нахождения седловой точки.
Имеем нелинейную систему решений, которая требует специальных методов.
Проверим крайние точки множества ограничений на удовлетворение этой системы.
Т.к.
при решении системы при различных
,
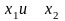были получены отрицательные
,
значит
ни одна из краевых точек, не является
седловой.
Решение системы.
> restart;
> Y1:=-8*x1+5*x2+4+4*L1+2*L2+3*L3+L4+L5;
> Y2:=5*x1-11.0*x2+10-2*L1+3*L2+3*L3+L6;
> Y3:=L1*(4*x1-2*x2+16);
> Y4:=L2*(2*x1+3*x2-40);
> Y5:=L3*(3*x1+3*x2-45);
> Y6:=L4*(x1-8);
> Y7:=L5*x1;
> Y8:=L6*x2;
> Y9:=(L1>=0);Y10:=(L2>=0);Y11:=(L3>=0);Y12:=(L4>=0);Y13:=(L5>=0);Y14:=(L6>=0);
> solve({Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8,Y9,Y10,Y11,Y12,Y13,Y14},{L1,L2,L3,L4,L5,L6,x1,x2});
