1.3.6. Зонная структура некоторых полупроводников

Расчёт зонной структуры твердых тел затруднён т.к. отсутствуют аналитические выражения для потенциала V(r). Поэтому при любых расчётах, в формулах содержаться некоторые параметры, значения которых определяются экспериментально. Например, ширина запрещенной зоны и эффективная масса определяется только из экспериментов; в частности, величину и ориентационную зависимость m^* определяют из экспериментов по циклотронному резонансу.

Имеющиеся к настоящему времени данные о зонной структуре полупроводников получены на основе, как теоретических расчётов, так и экспериментальных работ. Рассмотрим зонную структуру некоторых полупроводников. Как видно из рисунка (рис. 1.52), каждая из зон состоит из 3-х подзон. Это противоречит тому, что валентную зону и зону проводимости формируют 4 электрона (подзон должно быть 4). Однако это противоречие объясняется тем, что зона проводимости и валентная зона основных полупроводников (Si, Ge, GaAs …) включают р-состояния, для которых в кристалле снимается вырождение, поэтому каждая из зон представляет собой наложение лишь 3-х различных подзон.

Из рис. 1.52 следует, что зависимости для разных направлений различны. Положение абсолютного минимума определяет дно зоны проводимости. В кремнии он лежит в направлении [100], поэтому имеется 6 эквивалентных минимумов энергии. В Ge – минимумы зоны проводимости лежат в направлениях <111>, поэтому имеется 8 эквивалентных минимумов. Минимум энергии для электронов и дырок называют иногда долинами. Поэтому говорят, что зона проводимости Si имеет 6 долин, а Ge – 8 долин.

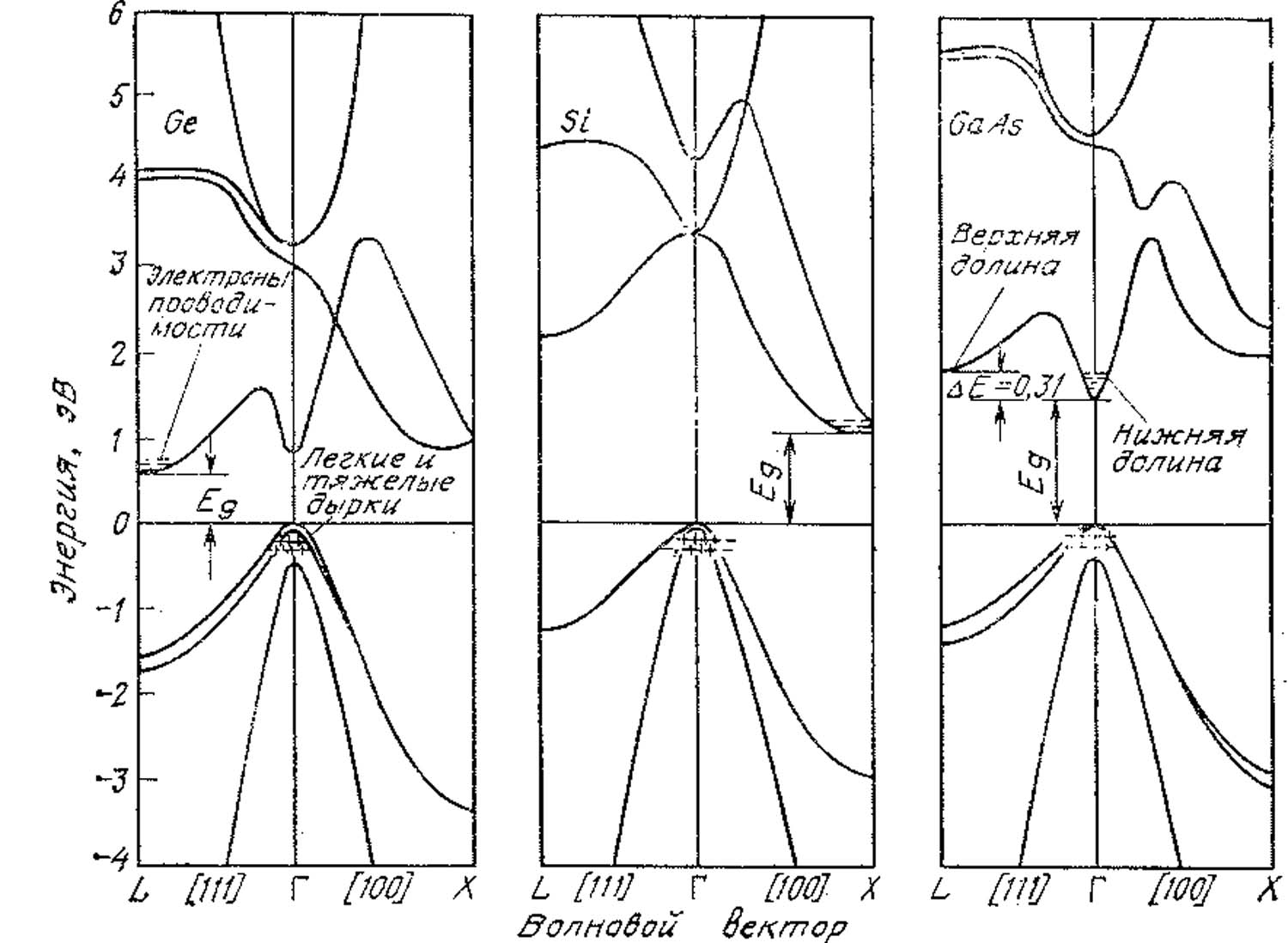
Рис.1.52.Структура энергетических зон Ge,Si и GaAs.

Изоэнергетические поверхности, т.е. поверхности равной энергии, около абсолютных минимумов представляют собой эллипсоиды вращения относительно большой полуоси. Зависимость энергии можно представить в виде:

(1.91)

Опыты по циклонному резонансу дают для компонентов тензора эффективной массы электрона в кремнии следующие значения

; :

здесь индекс t (transverse) обозначает поперечную составляющую эффективной массы, индекс l (longitudinal) – продольную (см. рис. 1.53).

E kl (а)	E kt (б)
Рис.1.53. Компоненты тензора эффективной массы зависят от локальной кривизны дисперсионной поверхности E(k). Малая кривизна поверхности E(k) соответствуем тяжелым электронам (случай (а)); большая кривизна – легким электронам (случай (б)).

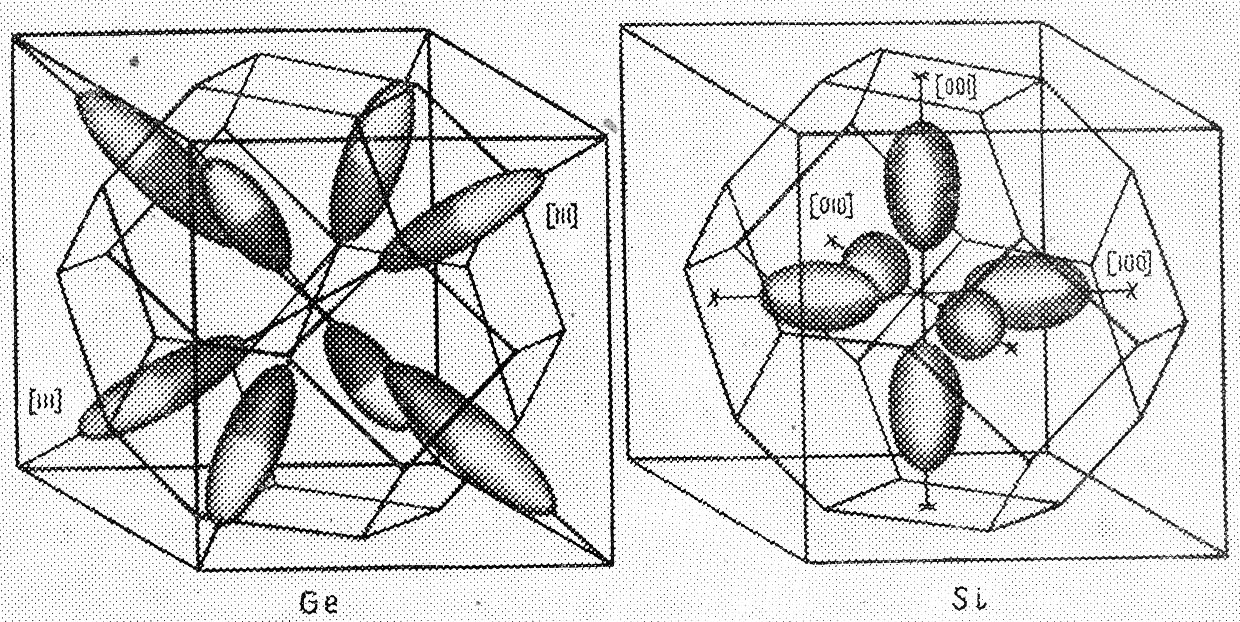
Эллипсоиды вращения изоэнергетических поверхностей в кремнии направлены в обратном пространстве таким образом, что большая полуось совпадает с направлениями <100>. Т.е. в кремнии имеется 6-кратное вырождение минимума (рис. 1.54). В германии – большие полуоси эллипсоидов вращения направлены вдоль направлений <111> (8-кратное вырождение). В GaAs – зона проводимости имеет форму сферы (рис. 1.54), т.е. эффективная масса электронов является скалярной величиной (содержит один компонент).

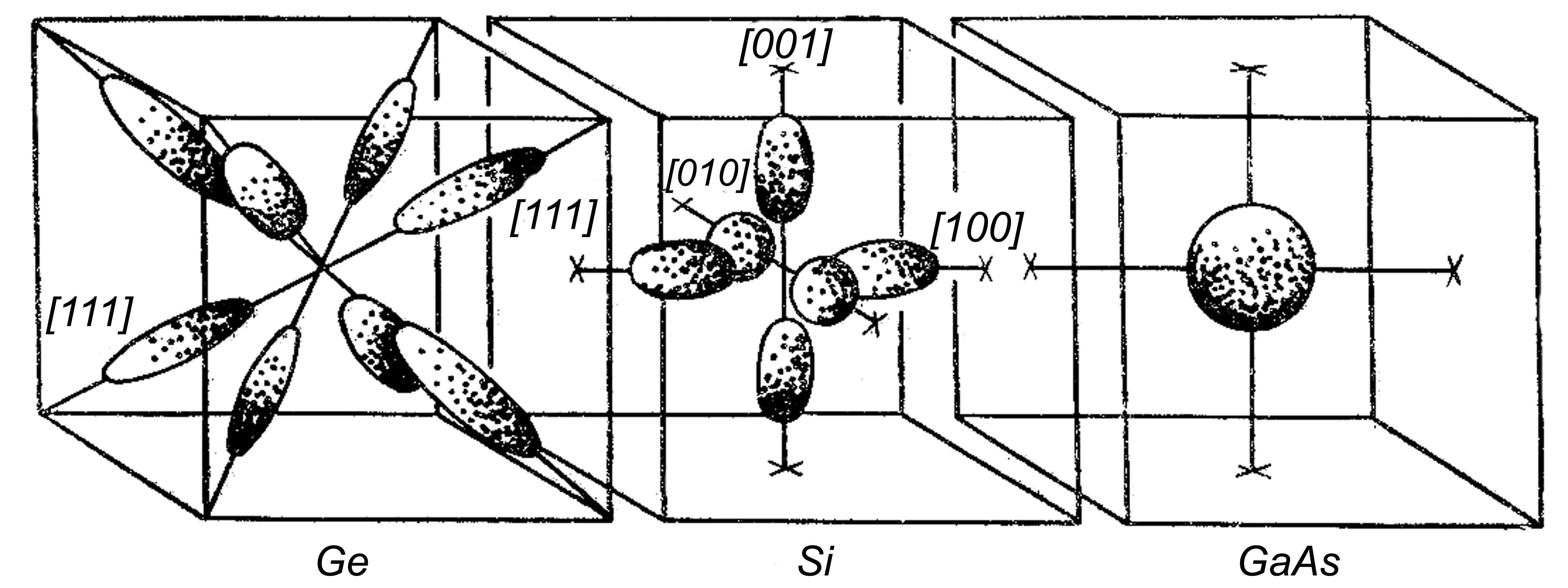
Рис. 1.54. Форма и расположение изоэнергетических поверхностей в Ge, Si и GaAs.

Точка минимума зоны проводимости у Si находится на расстояния 3/4 от центра до границы зоны Бриллюэна (рис. 1.55 а), у Ge – на краю зоны Бриллюэна (так, что эллипсоид минимальной энергии принадлежит одновременно и первой и второй зонам Бриллюэна, (рис. 1.55 б)), у GaAs – в центре зоны Бриллюэна.

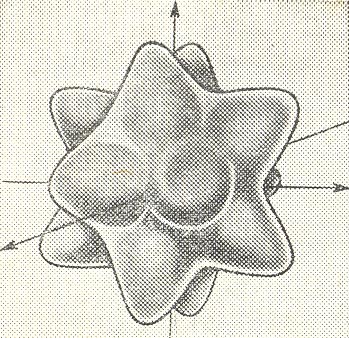
Рис. 1.55. Формы поверхностей постоянной энергии электронов в зонах проводимости Ge и Si. Внутри элементарной ячейки вписана первая зона Бриллюэна. Обратите внимание, что в Ge, эллипсоиды энергии расположены сразу в 2-х зонах Бриллюэна!	Рис. 1.56. Форма поверхности постоянной энергии тяжелых дырок в валентной зоне кремния.

Для валентной зоны максимум энергии находится в центре зоны Бриллюэна для всех трёх полос. При этом в точке все три зоны смыкаются, так что энергия в центре зоны Бриллюэна оказывается вырожденной (рис. 1.52). Учёт спин-орбитального взаимодействия приводит к тому, что вырождение частично снимается - одна из зон опускается на величину 0.035 эВ (рис. 1.52). Поверхности равной энергии дырок в валентной зоне представляют собой весьма сложные по виду гофрированные поверхности (рис. 1.56).

Минимальное расстояние между, дном зоны проводимости и потолком валентной зоны называется шириной запрещённой зоны. Для Si и Ge, как видно из рис. 1.52, минимум зоны проводимости и максимум валентной зоны лежат в разных точках зоны Бриллюэна, т.е. при различных значениях k.

Такие полупроводники, у которых минимум зоны проводимости и максимум валентной находятся при различных значениях k, называются непрямозонными. К их числу относится Si, Ge и др. (рис. 1.52 а, б). Полупроводники, для которых минимальное значение зоны проводимости и максимальное значение валентной зоны лежит при одном и том же k, называются прямозонными. Типичными представителями прямозонных полупроводник являются InSb, InP, GaAs (рис. 1.52в).

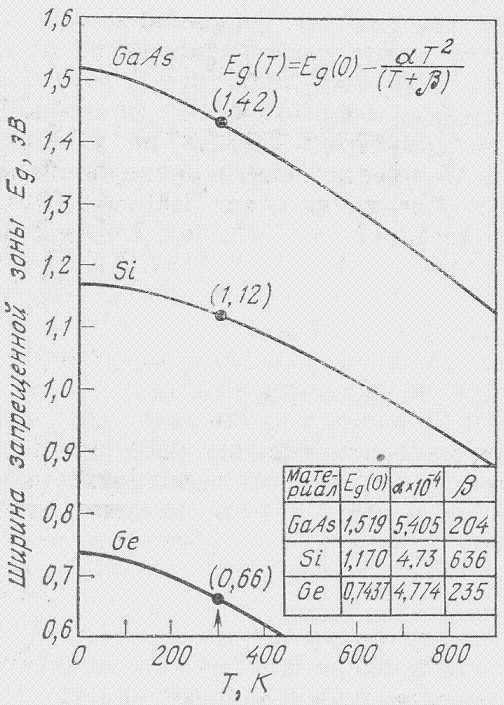
Из оптических и электрических исследований свойств полупроводников следует, что положение и ширина энергетических зон и примесных уровней зависят от температуры. Ширина запрещенной зоны большинства полупроводников уменьшается с увеличением температуры (рис. 1.57). Однако имеется несколько полупроводников (PbS, PbSe, Te), у которых повышение температуры сопровождается увеличением ширины запрещенной зоны.

1. Температурная зависимость ширины запрещенной зоны связана в основном с двумя эффектами. Во-первых, при нагревании кристалла увеличивается расстояние между узлами решетки, следовательно, изменяется вид потенциальной функции. Как было показано в модели Кронига и Пенни, чем больше размеры потенциальной ямы для электрона, тем шире зоны разрешенной энергии и меньше расстояние между ними. В пределе запрещенная зона исчезает полностью. При высоких температурах расширение решетки происходит пропорционально температуре, а при низких – по более сложному закону. Для некоторых алмазоподобных полупроводников в определенном температурном интервале коэффициент расширения принимает даже отрицательные значения.

Рис.1.57.Температурная зависимость ширины запрещённой зоны в Ge,Si и GaAs.

2. С увеличением температуры растет интенсивность колебаний решетки и увеличивается электрон-фононное взаимодействие, приводящее к смещению потолка валентной зоны и дна зоны проводимости. Расчеты показывают, что это дает основной вклад в температурную зависимость запрещенной зоны. При температурах Т<<Q, где Q - температура Дебая, ширина запрещенной зоны пропорциональна Т², а если Т>>Q, то ширина запрещенной зоны линейно зависит от Т.

Варшни И.П. показал, что наблюдаемую на опыте температурную зависимость ширины запрещенной зоны для алмаза, кремния, германия, карбида кремния, арсенида галлия, фосфида индия и арсенида индия можно выразить эмпирической формулой

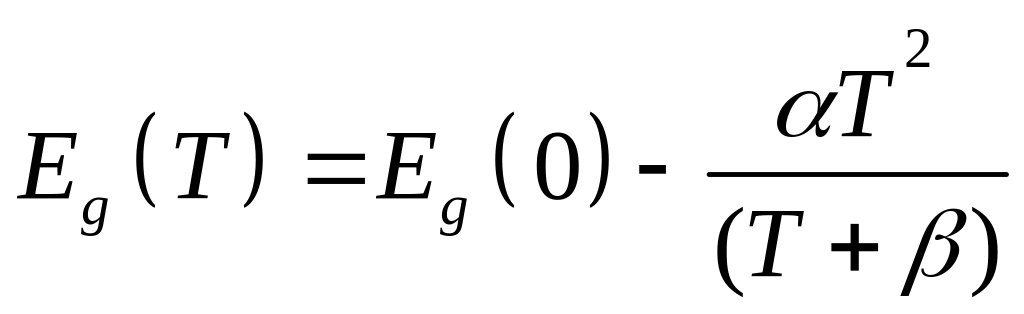, (1.92)

где - ширина запрещенной зоны при Т=0; a, b - параметры.