Последовательность расчёта

1. Изобразить в масштабе схему фермы. Указать размеры и нагрузки.

2. Построить расчётную схему фермы, заменив связи реакциями связей. Определить опорные реакции. Определить «нулевые стержни» по признакам « нулевых стержней».

3. Применяя метод вырезания узлов, определить усилия во всех стержнях фермы.

4. Определить усилия в стержнях фермы, применив метод сечений для трёх сечений.

5. Сравнить результаты в табличной форме.

Пример расчёта

Задание: Определить усилия во всех стержнях фермы.

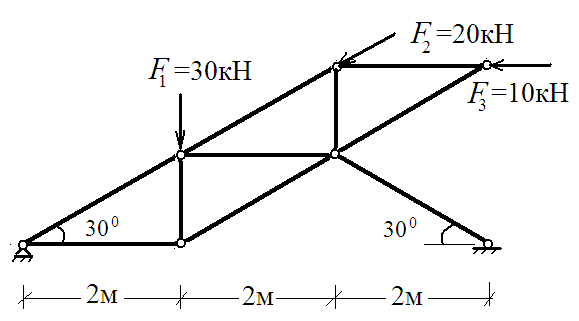
• Строим расчётную схему фермы. Освобождаем её от связей, заменяя их реакциями связей. Определяем высоту фермы.

Из ∆ ACD: AC = 2CD; AC ∙ cos α = AD;

AC = AD/cos α = 2/0.866 = 2.31м; CD = 2.31/2 = 1.155м;

EB = 2CD = 2.31м.

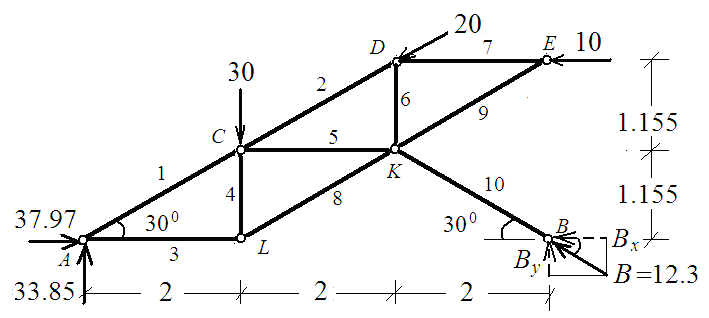
• Определяем опорные реакции:

∑М_А = 0; -30 ∙ 2 + 10 ∙ 2.31 + В sin 30⁰ ∙ 6 = 0; -36.9 + 0.5 В ∙ 6 = 0;

В = 12.3 кН;

∑ Y = 0; A_y - 30 - 20 sin 30⁰ + В sin 30⁰ = 0;

A_y = 30 + 20∙ 0.5 – 12.3 ∙ 0.5; A_y = 33.85 кН;

∑ X = 0; A_x - 20 cos 30⁰ – 10 - B cos 30⁰ = 0;

A_x = 20 ∙ 0.866 +10 + 12.3∙ 0.866; A_x = 37.97 кН;

Проверка: ∑М_D = 0; - A_y ∙ 4 + A_x ∙ ∙2.31 + 30 ∙ 2 + В∙cos 30⁰ ∙ 2 =

- 33.85 ∙ 4 + 37.97 ∙ 2.31 + 60 – 12.3 ∙ 0.866 ∙ 2.31 + 12.3 ∙ 0.5 ∙ 2 =

159.93 – 160 = 0.07; % ошибки: 0.07∙ 100% / 160 = 0.04% < 1%.

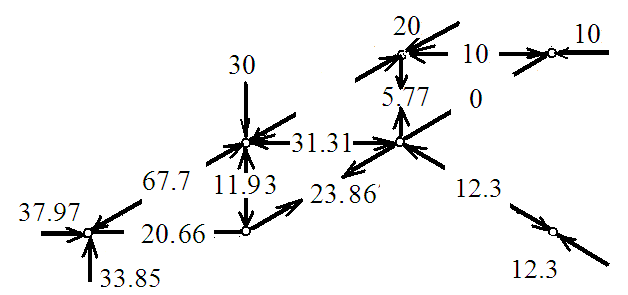
• Определяем усилия в стержнях фермы методом вырезания узлов. Расчёт начинаем с узла с двумя неизвестными. Это узлы Е и А.

Узел В: R₁₀ = 12.3 кН (стержень сжат);

Узел Е: R₉ = 0; (по признаку «нулевых стержней).

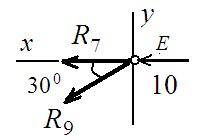
R₇ = -10 кН (стержень сжат);

Узел А:

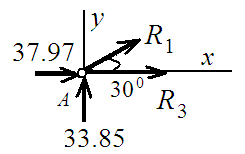
∑ Y = 0; R₁ sin 30⁰ + 33.85 = 0;

R₁ = - 67.7 кН (стержень сжат);

∑ X = 0; R₁cos 30⁰ + R₃ + 37.97 = 0; R₃ = 67.7 ∙ 0.866 – 37.97;

R₃ = 20.66 кН (стержень растянут);

Узел L:

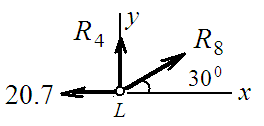
∑ X = 0; R₈ cos 30⁰ – 20.66 = 0; R₈ ∙ 0.866 = 20.66;

R₈ = 23.86 кН (стержень растянут);

∑ Y = 0; R₄ + R₈ sin 30⁰ = 0; R₄ = - 23.86 ∙ 0.5;

R₄ = - 11.93 кН (стержень сжат);

Узел D:

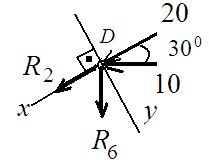
∑ Y = 0; R₆ cos 30⁰ - 10 ∙ sin 30⁰ = 0; R₆ ∙ 0.866 - 10 ∙ 0.5;

R₆ = 5.77 кН (стержень растянут);

∑ X = 0; R₂ + 20 + 10 cos 30⁰ + R₆ sin 30⁰ = 0;

R₂ = - 20 -10 ∙ 0.866 - 5.77 ∙ 0.5;

R₂ = - 31.55 кН (стержень сжат);

Узел С:

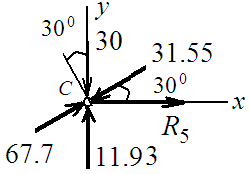
∑ X = 0; R₅ – 31.55 ∙ 0.866 + 67.7 ∙ 0.866 = 0;

R₅ = - 31.31 кН (стержень сжат);

• Определяем усилия в стержнях фермы методом сечений.

Выбирая тип уравнения, будем стремиться к тому, чтобы в него входило только искомое неизвестное усилие.

Предполагаем, что неизвестные усилия положительны (растянуты).

Сечение 1: ось Y перпендикулярна АС:

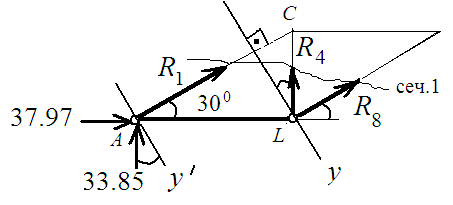
∑М_L ^низ. = 0; 33.85∙ 2 + R₁ sin 30⁰ ∙ 2 = 0; R₁ = 33.85/ 0.5;

R₁ = - 67.7 кН (стержень сжат);

∑ Y ^низ. = 0; 33.85 cos 30⁰ – 37.97 sin 30⁰ - R₄ cos 30⁰ = 0;

R₄ = 33.85 ∙ 0.866 – 37.97 ∙ 0.5;

R₄ = - 11.93 кН (стержень сжат);

∑ М_С ^низ. = 0; - 33.85 ∙ 2 + 37.97 ∙ 1.155 + R₈ cos 30⁰ ∙ 1.115 = 0;

R₈ = 23.84 кН (стержень растянут);

Сечение 2: ось Y перпендикулярна СD:

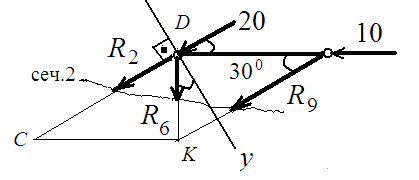
∑ М_К ^верх. = 0; R₂ cos 30⁰ ∙ 1.155 + 20 cos 30⁰ ∙ 1.155 - 10 ∙ 1.155 = 0;

R₂ = - 31.55 кН (стержень сжат);

∑ Y ^верх. = 0; R₆ cos 30⁰ - 10 sin 30⁰ = 0; R₆ = 5/ 0.866;

R₆ = 5.77 кН (стержень растянут);

∑М_D ^верх. = 0; R₉ = 0;

Сечение 3: ось Y перпендикулярна СА:

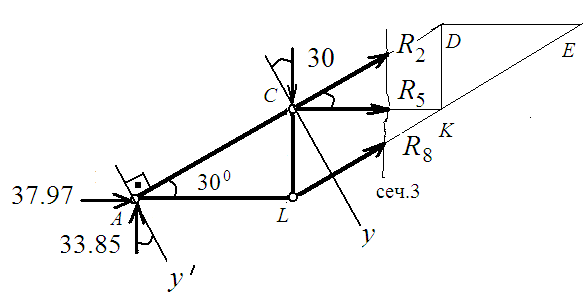
∑ Y ^низ. = 0; R₅ sin 30⁰ - 33.85 cos 30⁰ + 37.97 sin 30⁰ + 30 cos 30⁰ = 0;

R₅ = (3.85∙ 0.866 – 37.97∙ 0.5)/ 0.5;

R₅ = - 31.3 кН (стержень сжат);

• Сравниваем результаты расчётов в таблице:

№ стернжня	Усилие в стержне в кН (метод вырезания узлов)	Усилие в стержне в кН (метод сечений)	% ошибки
R1	- 67.70	- 67.70	0
R2	-31.55	-31.55	0
R3	20.66	-	-
R4	-11.93	-11.93	0
R5	-31.31	-31.30	0.32
R6	5.77	5.77	0
R7	-10	-	-
R8	23.86	23.84	0
R9	0	0	0.08
R10	12.30	12.30	-

24