6.Проверка гипотезы о независимости последовательности результатов измерений

Критерий знаков.

Пусть получено 20 измерений случайной величины X таблица 6.

Таблица 6 Исходная выборка

18,634	18,292	18,141	18,348	17,617	17,93	17,036	17,441	15,943	17,834
18,104	18,712	16,776	19,536	17,905	17,148	15,86	17,725	18,048	17,012

Построим вариационный ряд таблица 7

Таблица 7 Вариационный ряд

15,86	15,943	16,49	16,509	16,571	16,745	16,776	16,783	16,98	16,983
17,004	17,012	17,036	17,09	17,148	17,199	17,222	17,238	17,252	17,285

Серединная медиана Me = = 16,9935

Получим последовательность знаков

++++++++-+++-+++-+++

Число серий r₀ = 7

R_N,1-α/2 = R_20;0,975 = 6

R_N,α/2 = R_20;0,025 = 15

Так как 6 15, то по критерию знаков гипотеза о независимости последовательности результатов принимается.

Критерий Тренда.

Найдем число инверсий J₁ = 17 , J₂ = 15, J₃ = 14, J₄ = 14, J₅ = 7, J₆ = 10, J₇ = 4, J₈ =5 , J₉ = 1, J₁₀ = 5, J₁₁ = 6, J₁₂ = 7, J₁₃ = 1, J₁₄ = 6, J₁₅ = 4, J₁₆ = 2, J₁₇ = 0, J₁₈ = 1, J₁₉ = 1.

Общее число инверсий J₀ = 120

J_N,1-α/2 = J_20;0,975 = 64

J_N,α/2 = J_20;0,025 = 125

Полученное число 120 входит в область принятия гипотезы. Следовательно,

по критерию Тренда гипотеза о независимости последовательности принимается.

Построим график независимости последовательности результатов измерения(рис.3)

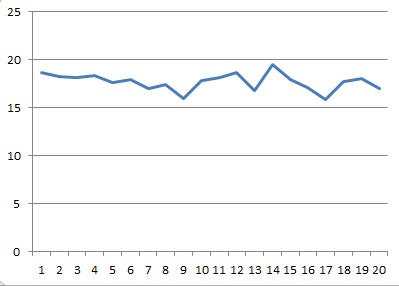
Рис.3 График независимости последовательности результатов измерения