2. Построение эквипотенциалей

Для построения эквипотенциалей с помощью первого метода предлагается следующий алгоритм:

1

Рис.11

)для эквипотенциальных линий шаг перпендикулярен вектору поля, поэтому пересчет координат осуществляется по схеме: (в формуле для можно взять знак “-“, тогда в формуле для должен быть “+” );

2

Рис.4

) для выбора точек старта предварительно находятся min, max значения потенциала в рассматриваемой области и формируется массив промежуточных значений потенциала для различных эквипотенциалей;

3) точка старта с необходимым потенциалом ищется на силовой линии. Чтобы не потерять эквипотенциали типа “восьмерок” необходимо стартовать несколько раз с различных линий, выходящих из положительного заряда в разные стороны;

4) линию обрываем в следующих случаях: а)"накрутился" угол больше 2 вокруг одного из зарядов, (для эквипотенциалей типа “восьмерка” необходимо брать больший ограничитель по углу, иначе некоторые линии разрываются), б) точка "убежала" за экран и при новом старте в обратную сторону снова "убежала" за экран, в)поле E "очень мало", г)расстояние до точки старта мало, (линия замкнулась).

Следует отметить, что даже такой усложненный алгоритм имеет недостатки и требует введения дополнительных условий для избежания повторного построения линий при наличии нескольких зарядов (N>3).

Н

Рис.12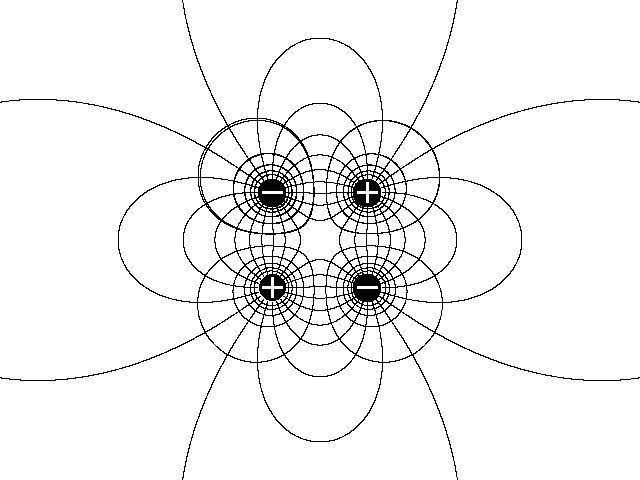

а рис.12 представлена картина поля четырех знакочередующихся зарядов (квадруполя). Несмотря на все ухищрения, на рис.12 виден недостаток – эквипотенциали вокруг верхнего отрицательного заряда двоятся. Отметим, что такого типа недостатки проявляются не всегда, например, для поля заряженного отрезка, представленного на рис.13, никаких трудностей нет.

П

Рис.6

Рис.13

оле равномерно заряженного отрезка вычислялось по формуле , - линейная плотность заряда, - кратчайшее расстояние от точки наблюдения до отрезка, - угол между прямыми, проведенными в точку наблюдения из концов отрезка, поле - направлено по биссектрисе этого угла.

Для построения эквипотенциалей с помощью второго метода предлагается следующий алгоритм. Видимая область экрана разбивается на прямоугольные элементы. Вычисляются координаты вершин прямоугольников и значения потенциала в этих точках. После этого проверяется условие попадания значения потенциала, соответствующего данной эквипотенциали в интервал значений потенциала для двух соседних вершин прямоугольника. Если значение потенциала попадает в границы интервала, то с помощью линейной интерполяции вычисляются координаты точки на границе, соответствующие этому значению потенциала. После нахождения второй точки проводится отрезок прямой, соединяющий две точки с заданным значением потенциала.

2.3.3. Поле системы зарядов в дальней зоне.

Электрический диполь и квадруполь

В

дальней зоне потенциал можно представить в виде: , где: монополь, диполь, квадруполь. Имеют место следующие равенства: , , где по определению вектор называется электрическим моментом системы зарядов,

Для двух зарядов имеет вид , и направлен от отрицательного заряда к положительному.

Поле в дипольном приближении имеет вид: .

Потенциал поля в квадрупольном приближении равен: ,

где симметричный тензор 2-го ранга в трёхмерном пространстве, .