2. Уравнения Максвелла как результат обобщения опытных фактов Метрологический способ введения первичных понятий эд

Как известно, одной из основных единиц СИ является «ампер», а единица измерения заряда – «кулон» является производной единицей. В метрологии принят непрямой способ определения заряда через величину постоянного тока . Заряд, переносимый через поперечное сечение проводника, равен произведению силы тока на время его прохождения через это сечение.

Сила тока определяется через магнитное взаимодействие двух длинных параллельных проводников с током.

Ампер равен величине стационарного тока, который, будучи пропущен по двум параллельным бесконечно длинным проводникам, расположенным в вакууме на расстоянии 1 м создаёт силу взаимодействия Н на метр длины проводника.

В

ектор магнитной индукции может быть определен с помощью значения максимальной силы, действующей на отрезок проводника с током.

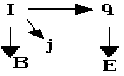
Общая схема введения основных понятий ЭД с помощью метрологического подхода имеет следующий вид, где - плотность тока, - напряженность электрического поля.

Аксиоматический способ введения основных понятий эд

При аксиоматическом подходе первичной физической величиной в ЭД может быть выбран заряд.

Удобно ввести понятие плотности тока с помощью равенства:

, где - средняя скорость движения заряженных частиц под действием электромагнитного поля, -объемная плотность заряда.

М

одуль плотности тока численно равен заряду, проходящему в единицу времени через единицу площади поверхности перпендикулярно траектории движения зарядов. В таком случае ток - это поток плотности тока .

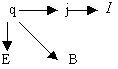
Далее основные понятия ЭД можно вводить в следующем порядке:

2.2.1. Закон сохранения заряда

Первоначальное представление о заряде складывалось как представление об электрической жидкости, перетекающей от одного тела к другому. Поэтому естественной оказалась и гипотеза о сохранении заряда при взаимодействии тел. Аналогичная ситуация с теорией теплорода, но там закон сохранения не работает (тепло не является видом энергии).

Заряд - это одновременно 1) субстанция, 2) свойство тел взаимодействовать определённым образом, 3) число, приписываемое по определённому правилу

Закон сохранения заряда в интегральной форме можем записать в

в

иде , или

где I- ток, вытекающий из некоторой замкнутой поверхности,

- неподвижный объём, ограниченный замкнутой поверхностью S.

Смысл этого уравнения таков, что заряд меняется только за счёт втекания или вытекания тока из объёма V.

2.2.2. Закон Кулона. Электростатическая теорема Гаусса

Ф

Сила электростатического взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль прямой линии, соединяющей эти заряды

ормулировка закона Кулона (1785 г.).

Нетрудно заметить, что зависимость силы от величины заряда может быть проверена экспериментально, только если предварительно постулирован закон сохранения заряда, иначе эта зависимость носит характер условного соглашения. Например, можно было бы утверждать, что сила пропорциональна произведению квадратов зарядов. Более строго электростатика может быть построена с помощью следующих утверждений:

1) Транзитивность^* отталкивания - (опытный факт), притяжение не транзитивно (если А отталкивает Б и Б отталкивает С, то Б отталкивает А);.

2) - (опытный факт), (доказали: Кавендиш – с помощью опыта с полусферами , Кулон - с помощью крутильных весов);

3) Отношение модулей сил взаимодействия двух любых частиц с третьей не зависит от выбора последней - (обобщённый опытный факт);

4) 3-ий закон Ньютона - постулируется;

5) Принцип суперпозиции, связан с утверждением 3, можно считать обобщённым опытным фактом.

Закон Кулона может быть записан следующим образом:

где .

Закон Кулона позволяет ввести напряжённость электрического поля

, где -пробный заряд (малый заряд не вызывающий перераспределения зарядов на других телах).

При этом выражение для напряженности поля точечного заряда принимает вид: где: -электрическая постоянная.

Теорема Гаусса (электростатическая)

Вычислим поток электрического поля через элементарную площадку . По определению потока (скалярного) . Подставив выражение для напряженности поля точечного заряда, получим: ,

где - элемент телесного угла, под которым видна площадка из точки расположения заряда.

Для потока электрического поля через произвольную замкнутую поверхность получим: , где телесный угол равен:

В общем виде теорема Гаусса для поля в вакууме имеет вид

и читается так:

поток электрического поля через произвольную замкнутую поверхность равен отношению суммарного заряда, находящегося внутри этой поверхности, к электрической постоянной

Вычисление электростатических полей с помощью теоремы Гаусса.

С помощью теоремы Гаусса можно вычислить поле только для нескольких примеров симметричного распределения зарядов.

Пример: Найти электрическое поле, создаваемое зарядом q, равномерно распределенным по объёму шара R.

Дополнение: Найти распределение плотности массы, создающей поле, .

Поле обладает центральной симметрией, выберем поверхность для вычисления потока в виде сферы радиуса r, тогда по теореме Гаусса для поля внутри шара имеем: 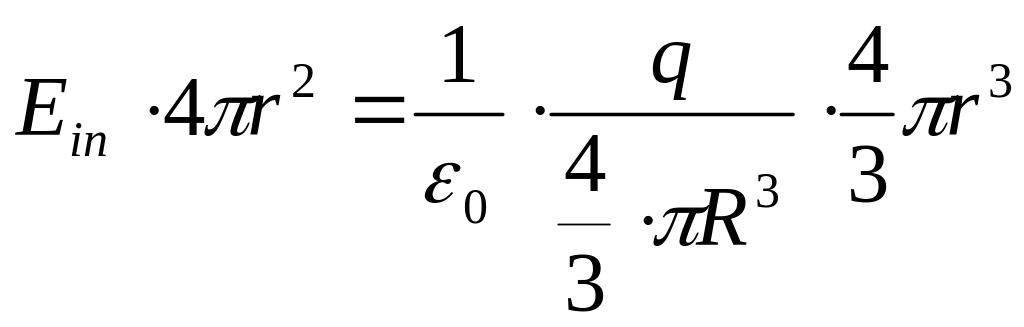откуда получаем: .

Для поля снаружи шара получаем: .