Определение усилия в раскосе
Для раскоса в рассматриваемом примере, как и в большинстве случаев расчета промежуточных опор, расчетным является аварийный режим односторонний обрыв провода на нижней левой траверсе (рис. 7.1) [5, 6].
В этом случае происходит кручение ствола опоры под действием крутящего момента (рис. 7.3, в)
Мк = Т lт, (7.21)
где T – тяжение нижнего левого провода при обрыве;
lT – длина (вылет) нижней левой траверсы.
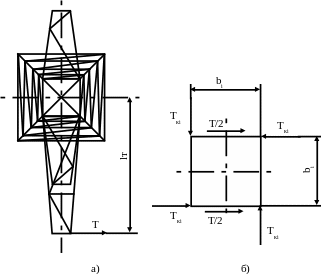
Рис. 7.3. Схема к расчету ствола одностоечной опоры на кручение
Подставляя в формулу (7.21) численное значение T и lT, получим
кНּм.
Крутящий момент MК, передающийся с траверсы на ствол с помощью диафрагм, установленных в местах крепления траверсы к стволу, нагружает все четыре грани опоры.
Действие крутящего момента MК при расчете элементов решетки заменяем действием двух пар сил Tкi, которые приложены непосредственно к граням опоры (рис. 7.3, б). Так как крутящий момент не изменяется по высоте ствола, то сила Tкi, составляющая пары, может быть определена в любом сечении ствола по формуле
,
(7.22)
если сечение ствола квадратное.
В рассматриваемом примере
кН.
Как видно из схемы совместного действия
тяжения T и пар сил Tкi
в одной из граней опоры, сила
(сила T делится на две
грани поровну) и сила Tкi
складываются (рис. 7.3, б). Эта грань опоры
и является расчетной.
Для определения усилия в раскосе составим расчетную схему наиболее нагруженной грани опоры (рис. 7.4). Жесткие узлы решетки условно заменяем идеальными шарнирами и считаем, что оси решетки проходят через центры этих шарниров. Все внешние нагрузки прикладываем в узлах системы: силу Tкi прикладываем в i-ом узле решетки, а силу в узле пересечения пояса боковой грани ствола с нижним поясом нижней траверсы.
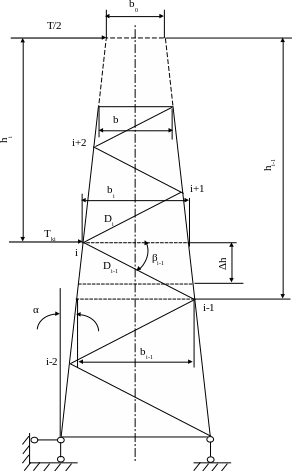
Рис. 7.4 Расчетная схема
X
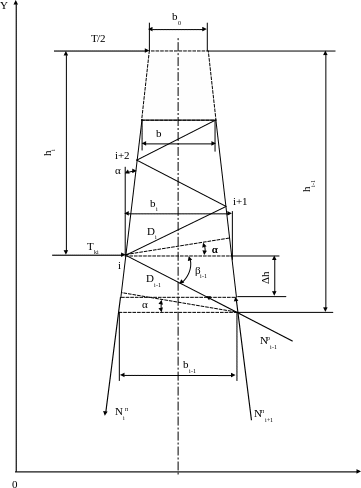
Рис. 7.5. Расчетная схема для определения усилий в стержнях формы с треугольной решеткой
Плоская ферма с треугольной решеткой, изображенная на рис. 7.4 является простейшей. Для определения усилий в стержнях простейших ферм используют метод сечений.
Рассечем ферму, изображенную на рис.7.4
по линии, пересекающей пояса и
рассчитываемый раскос и проходящий
ниже i-го узла на некотором
расстоянии Δh от него. В
этом случае рассчитываемый раскос –
нисходящий. Отсеченная часть фермы
(верхняя) будет уравновешена
системой внешних (Т/2 и Tкi)
и внутренних (
,
,
)
сил. Направление внутренних сил (рис.
7.5) принято действительное на основании
анализа действия внешних сил.
Для определения неизвестных усилий в поясах составим два уравнения моментов всех сил (внешних и внутренних) относительно узлов i и (i - 1) (рис. 7.4, 7.5):
,
;
ΣМi-1=
0,
.
Откуда усилие в правом поясе
,
(7.23)
а усилие в левом поясе
.
(7.24)
Проецируя на ось OY все силы, действующие на отсеченную часть фермы, получим следующее уравнение равновесия:
,
.
Отсюда усилие нисходящего от i-го узла раскоса
.
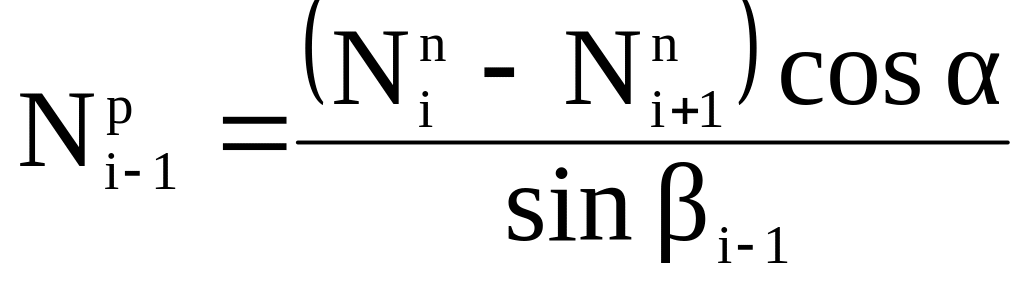(7.25)
Подставляя выражения (7.23) и (7.24) в (7.25), получим
.
(7.26)
Подставляя численные значения величин в формулу (7.26), получим
кН.
Итак, усилие в раскосе D8
кН.