Раздел 6

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ

Многообразие задач принятия решений (выбора).

Задачи принятия решений можно классифицировать по многим основаниям. По числу ЛПР выделяют задачи индивидуального и коллективного принятия решений. По виду показателя эффективности — однокритериальные и многокритериальные. По степени определенности информации — задачи выбора в условиях определенности и в условиях неопределенности. По структуре множества альтернатив — задачи условного выбора и задачи выбора на конечном множестве альтернатив. По степени информированности ЛПР — новые и повторяющиеся задачи. Кроме этих существует большое число других критериев классификации. Определение типа задачи помогает понять ее специфику и выбрать наиболее подходящие методы решения.

Выбор в условиях неопределенности.

Предположим, что ЛПР (лицо, принимающее решения) рассматривает несколько возможных решений: i = 1,…,m. Ситуация, в которой действует ЛПР, является неопределенной. Известно лишь, что наличествует какой-то из вариантов: j = 1,…, n. Если будет принято i-e решение, а ситуация есть j-я , то фирма, возглавляемая ЛПР, получит доход qij. Матрица Q = (qij) называется матрицей последствий (возможных решений). Какое же решение нужно принять ЛПР? В этой ситуации полной неопределенности могут быть высказаны лишь некоторые рекомендации предварительного характера. Они не обязательно будут приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но как оценить риск в данной схеме? Допустим, мы хотим оценить риск, который несет i-e решение. Нам неизвестна реальная ситуация. Но если бы ее знали, то выбрали бы наилучшее решение, т.е. приносящее наибольший доход. Т.е. если ситуация есть j-я , то было бы принято решение, дающее доход qij. Значит, принимая -e решение мы рискуем получить неqj, а только qij, значит принятие i-го решения несет риск недобрать rij = qj - qij. Матрица R = (rij) называется матрицей рисков. Пример 1. Пусть матрица последствий есть

Составим матрицу рисков. Имеем q1 = max(qi1) = 8, q2 = 5, q3 = 8, q4 = 12.. Следовательно, матрица рисков есть

Принятие решений в условиях полной неопределенности

Не все случайное можно "измерить" вероятностью. Неопределенность – более широкое понятие. Неопределенность того, какой цифрой вверх ляжет игральный кубик отличается от неопределенности того, каково будет состояние российской экономики через 15 лет. Кратко говоря, уникальные единичные случайные явления связаны с неопределенностью, массовые случайные явления обязательно допускают некоторые закономерности вероятностного характера. Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации. Какие же существуют правила-рекомендации по принятию решений в этой ситуации?

Правило Вальда (правило крайнего пессимизма). Рассматривая i-e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход ai Но теперь уж выберем решение i0 с наибольшим ai0. Итак, правило Вальда рекомендует принять решение i0, такое что  Так, в вышеуказанном примере, имеем a1 = 2, a2 = 2, a3 = 3, a4 = 1. Из этих чисел максимальным является число 3. Значит, правило Вальда рекомендует принять 3-е решение.

Правило Сэвиджа (правило минимального риска). При применении этого правила анализируется матрица рисков R = (rij). Рассматривая i-e решение будем полагать, что на самом деле складывается ситуация максимального риска bi = max [rij] Но теперь уж выберем решение i0 с наименьшим bi0. Итак, правило Сэвиджа рекомендует принять решение i0, такое что В рассматриваемом примере имеем b1 = 8, b2 = 6, b3 = 5, b4 = 7. Минимальным из этих чисел является число 5. Т.е. правило Сэвиджа рекомендует принять 3-е решение.

Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). Принимается решение i, на котором достигается максимум ,где 0 ≤ λ ≤ 1. Значение λ выбирается из субъективных соображений. Если λ приближается к 1, то правило Гурвица приближается к правилу Вальда, при приближении λ к 0, правило Гурвица приближается к правилу "розового оптимизма" (догадайтесь сами, что это значит). В вышеуказанном примере при λ= 1/2 правило Гурвица рекомендует 2-е решение.

Принятие решений в условиях частичной неопределенности

Предположим, что в рассматриваемой схеме известны вероятности pj того, что реальная ситуация развивается по варианту j. Именно такое положение называется частичной неопределенностью. Как здесь принимать решение? Можно выбрать одно из следующих правил. Правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации i-го решения, является случайной величиной Qi с рядом распределения

qi1	qi2	…	qin
p1	p2	…	pn

Математическое ожидание M[Qi] и есть средний ожидаемый доход, обозначаемый . Правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход. Предположим, что в схеме из предыдущего примера вероятности есть (1/2, 1/6, 1/6, 1/6). Тогда Максимальный средний ожидаемый доход равен 7, соответствует третьему решению. Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации i-го решения, является случайной величиной Ri с рядом распределения

ri1	ri2	…	rin
p1	p2	…	pn

Математическое ожидание M[Ri] и есть средний ожидаемый риск, обозначаемый также . Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск. Вычислим средние ожидаемые риски при указанных выше вероятностях. Получаем  Минимальный средний ожидаемый риск равен 7/6, соответствует третьему решению. Анализ принимаемых решений по двум критериям: среднему ожидаемому доходу и среднему ожидаемому риску и нахождение решений, оптимальных по Парето, аналогично анализу доходности и риска финансовых операций. В примере множество решений, оптимальных по Парето операций, состоит только из одного 3-его решения. В случае, если количество Парето-оптимальных решений больше одного, то для определения лучшего решения  применяется взвешивающая формула .

Задача выбора альтернатив.

Задачи принятия решений существенно различаются в зависимости от требований, которые предъявляются к виду окончательного решения. По этому признаку можно выделить три основных класса задач — классификации альтернатив, ранжирования альтернатив и выбора наилучшей альтернативы. В задачах классификации альтернатив в результате решения все альтернативы разделяются на некоторые группы (классы), которые упорядочиваются ЛПР по их предпочтительности, но в пределах каждой группы альтернативы считаются равноценными. Разделение каких-либо объектов на группы часто встречается на практике, особенно в тех случаях, когда этих объектов достаточно много. Как правило, нет смысла и практически сложно упорядочить все объекты, если их число достигает нескольких десятков или сотен. В таких случаях разбиение на группы служит вполне удовлетворительным решением задачи или рассматривается как предварительный шаг для более глубокого анализа. Например, товары можно группировать по их качеству, рынки сбыта— по уровню спроса, виды деятельности — по их прибыльности или престижности, предприятия и фирмы — по их репутации или надежности. Однако существуют задачи, в которых недостаточно разделить объекты на группы, а требуется строго упорядочить их по предпочтительности. Они называются задачами упорядочения, или ранжирования альтернатив. Так, например, руководители организаций могут ранжировать текущие задачи и планы работ по степени важности, своих подчиненных — по уровню квалификации, варианты инвестиций— по сроку окупаемости или ожидаемой прибыли. В общем случае требование упорядочения альтернатив означает, что ЛПР хочет определить относительную ценность каждой из них. Это довольно сложная и трудоемкая задача для человека. Поэтому часто она упрощается, когда люди отказываются от строгого ранжирования, где все альтернативы как бы «построены» одна за другой, и пытаются найти квазипорядок, где некоторые альтернативы считаются равноценными или несравнимыми между собой. Традиционной задачей принятия решений считается задача выбора наилучшей альтернативы. Она наиболее часто встречается на практике. В данном случае термин «наилучшая» не обязательно означает «оптимальная». Это может быть удовлетворительное решение, выбранное из исходного множества альтернатив, но это решение должно быть единственным. После того, как выбор сделан, относительная ценность других решений значения не имеет. Как правило, задача выбора наилучшей альтернативы возникает, когда число альтернатив невелико и обозримо для ЛПР.

ЛПР(лица, принимающие решение)

Оптимизация

Одна из наиболее злободневных проблем анализа систем, рассматриваемых в сициально-экономических задачах, — это проблема выбора критерия, т.е. вопрос о том, каким образом следует сравнивать между собой различные реализации поведения систем. К счастью, динамические процессы, наблюдаемые в физических и биологических системах, часто протекают по вполне определенным законам, которые, как правило, являются следствием различных принципов минимума или законами сохранения. Однако перенос этих законов на объекты социальной природы в лучшем случае носит искусственных характер и, более того, часто просто невозможен. Поскольку цель нашего курса состоит в изучении структуры систем независимо от вопросов оптимизации, можно позволить себе роскошь оставить в стороне проблему выбора критерия. Тем не менее, для того, чтобы продемонстрировать значимость этой проблемы, рассмотрим простой пример, иллюстрирующий ситуацию, когда выбор различных критериев приводит к качественно различным стратегиям управления.

Предположим, что динамика системы описывается одномерным линейным дифференциальным уравнением dx/dt = u(t), x(0) = c, где u(t) — вход, или функция управления. Предположим, далее, что доступные резервы управления ограничены следующим образом:

|u(t)| ≤ 1 для всех 1 t ≥ 0

(Подобная ситуация возникает, например, при управлении автомобилем, и тогда функция u(t) есть скорость движения.)

Одним из критериев для данного процесса может быть перевод системы из начального состояния с в некоторое заданное состояние, например, x = 0 за минимальное время. Хорошо известно, что решение этой задачи имеет вид:

u(t) = +1, c < 0, u(t) = -1, c > 0

т.е. релейное управление является оптимальным. Предположим теперь, что мы стремимся минимизировать квадратичный функционал этого вида вида. Можно показать, что в этом случае оптимальный закон управления имеет вид u(t) = th(T-t)⋅x(t), и он может быть реализован в виде обратной связи или синтеза.

Полученные результаты показывают, что изменение критерия качественно меняет характер решения. В первом случае мы имеем экстремальные управления, переключающиеся с одной границы на другую в зависимости от начального состояния. Во втором случае оптимальный закон управления строится по ходу развития самого процесса и не имеет никаких точек разрыва. Важно отметить, что, хотя динамика системы остается неизменной, выбор иного критерия приводит к качественному изменению оптимального управления.

Функция полезности как критерий оценки товаров

Отношение предпочтения, рассмотренное в предыдущем параграфе, является весьма неудобным инструментом изучения потребительского выбора. Оно является больше качественной категорией и не приспособлено для проведения количественных исследований. Поэтому нужен другой механизм, который, с одной стороны, был бы адекватен данному отношению предпочтения, то есть отражал бы все его основные свойства, с другой стороны, являлся бы численным индикатором отношения предпочтения. Таким механизмом и является функция полезности. С функцией работать удобнее, чем с отношением предпочтения, хотя последнее имеет и определенные преимущества. Если отношение предпочтения отражает "склонность" или "желание" потребителя, то функция полезности отражает понятие "выгодности" товаров. Полезность понимается как мера благосостояния и как критерий правильности принимаемых решений. Источником полезности является потребление товара. Термин "полезность" менее индивидуален, чем термин "предпочтение". Действительно, труднее угадать, что человеку хочется, чем определить что ему полезней, так как факт "х полезнее у", в отличии от "х предпочтительнее у", можно оценить по числовой шкале.

Функция полезности должна быть построена с учетом всех тех объективных и субъективных условий, которые влияют на предпочтение потребителя. Например, полезность денег оценивается не только их покупательской способностью. Так, с большой степенью уверенности можно утверждать, что полезность десяти заработанных долларов больше, чем те же десяти долларов найденных случайно на улице. Для наркомана "полезность" набора товаров тем выше, чем больше в нем содержится героина, а для нормального человека - наоборот. При построении функции полезности все эти нюансы, связанные с понятием полезности, учитываются тем обстоятельством, что эта функция строится сугубо на основе отношения предпочтения, то есть каждому отношению предпочтения соответствует своя функция полезности.

Перейдем к строгим определениям.

Определение 3.1. Пусть в   определено отношение предпочтения   . Любая функция   такая, что   тогда и только тогда, когда   , называется функцией полезности, соответствующей этому отношению предпочтения.

Если интересы потребителя ограничиваются множеством   , то функция полезности определяется на этом множестве,   .

В терминах функции полезности отношение безразличия   задается равенством   .

Всегда ли можно представить отношение предпочтения функцей полезности? Можно ли исходя из предпочтения   найти функцию u, удовлетворяющую определению 3.1 ? Отвечая на этот вопрос приведем без доказательства следующее утверждение (доказательство можно найти, напр., в [ 18 ]).

Теорема 3.1. Для любого отношения предпочтения, определенного и непрерывного в   , можно построить представляющую его (непрерывную) функцию полезности  .

Оказывается. что для люього непрерывного отношения предпочтения можно построить целое семейство функций полезности. Этот факт сформулируем в виде следующего утверждения.

Теорема 3.2. Пусть  - функция полезности, представляющая отношение предпочтения   . Для любой строго возрастающей функции   сложная функция (суперпозиция)   является функцией полезности, так же представляющей это отношение предпочтения   .

В качестве упражнения, для двух строго возрастающих функций   проверьте справедливость этой теоремы.

Заметим, что для потребителя все эти функции полезности равнозначны. Он не в состоянии отдать предпочтение одной из них перед множеством возможных других, так как все они отражают одно и то же отношение предпочтения. Различие этих функций касается различных "масштабов" измерения полезности и не является принципиальным.

Так как функция полезности должна быть адекватной отношению предпочтения, то для нее можно сформулировать свойства а4), а5), а6). Например, в терминах функции полезности свойство ненасыщаемости читается так:

a'5) для любых   неравенство   влечет неравенство   и неравенства   ,   влекут   .

Из этого определения видно, что в случае ненасыщаемости функция u не достигает своего максимума на множестве Х: для любого  найдется   , который имеет большую полезность чем х.

Аналогом свойства а6) является вогнутость функции полезности:

a'6) для любых    .

Если в условии вогнутости имеет место строгое неравенство, то функция полезности называется строго вогнутой. В этом случае, как будет показано в § 3.3 , выбор потребителя определяется однозначно.

Преимущество функции полезности против отношения предпочтения состоит, в частности, в том, что для анализа потребительского выбора можно использовать мощный аппарат дифференцирования. Пусть функция полезности и дифференцируема и

Частная производная (3.2.1) называется предельной полезностью товара вида i. Это есть полезность, получаемая от "дополнительной" доли товара вида i:

Поэтому неравенство (3.2.1) можно интерпретировать так: для любого набора товаров   возрастание потребления товара вида i при постоянном уровне потребления других товаров приводит к увеличению полезности. Таким образом, (3.2.1) - это условие ненасыщаемости, написанное для дифференцируемой функции полезности. Забегая вперед скажем, что именно предельная полезность товара является определяющим цену товара фактором. Здесь нет противоречия с рыночным механизмом ценообразования, так как при прочих фиксированных условиях спрос на товар определяется его полезностью.

Предположим теперь, что функция u дважды дифференцируема и имеет непрерывные вторые частные производные. Для такой функции свойство строгой вогнутости выполнено, если матрица Гессе

отрицательно определена (см. (2.3.6)). Тогда, в частности, выполнены условия:

Это неравенство говорит о том, что предельная полезность   товара уменьшается по мере того, как продукт потребляется. Неравенство(3.2.1) и (3.2.2) отражают хорошо известный в экономической теории закон об убывающей предельной полезности (закон Госсена).

С понятием функции полезности неразрывно связано понятие кривых безразличия, имеющее широкое применение в математической теории потребления.

Определение 3.2. Кривой безразличия для данного набора товаров   называется геометрическое место точек   , которые находятся в отношении безразличия с этим набором х, то есть множество   .

Так как для всех точек из этого множества полезность одна и та же, то кривые безразличия задаются уравнениями  , где с - любая const. Таким образом, кривая безразличия математически представляется как линия уровня функции полезности. Поэтому для любой функции полезности существует бесконечное множество кривых безразличия (для разных const) и они заполняют все пространство   , образуя так называемую карту безразличия.

Приведем примеры некоторых, наиболее часто применяемых функций полезности и виды их карт безразличия. Эти функции, как показала практика, при определенных условиях достаточно объективно отражают предпочтение потребительского выбора.

1. Функция полезности с полным взаимозамещением благ:

где коэффициент   является числовой оценкой полезности от потребления единицы товара вида i. Для построения кривых безразличия функции (3.2.3) в   из уравнения   найдем

При постоянных   и   это есть семейство (по параметру с) параллельных прямых с углом наклона   .

Функция (3.2.3) учитывает возможность компенсации уменьшения потребления одних товаров другими.

Пример 3.3. Пусть товаром первого вида является кофе, второго – чай, а потребление этих продуктов в количествах   и   дает полезность, равную c , то есть   .

Представим, что потребление кофе уменьшилось на   единиц. Тогда полезность упадет до уровня   . Чтобы компенсировать эту потерю полезности надо увеличить потребление чая на величину   так, чтобы

Отсюда найдем   . В результате имеем:

Таким образом, функция (3.2.3) позволяет определить размер замещения одних товаров другими для того, чтобы полезность оставалась на неизменном уровне.

2. Функция полезности с полным взаимодополнением благ:

где   - количество товара вида i, приходящееся на единицу полезности. Для построения кривых безразличия функции (3.2.4) в   из уравнения

найдем

Отсюда видно, что карту безразличия функции (3.2.4) составляют одна линия, проходящая через начало координат и два семейства (по параметру с) линий, параллельных осям координат.

Функция (3.2.4) учитывает возможность дополнения одних товаров другими.

Пример 3.4. Приобретается набор из двух товаров: кофе в количестве   и сахар   в количестве c . Потребление этих товаров дает полезность, равную с, то есть

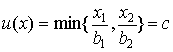
В случае (3.2.5)

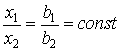
и увеличение (уменьшение) потребления кофе влечет увеличения (уменьшения) сахара.

В случае (3.2.6) увеличение потребления кофе может привести к нарушению неравенства в (3.2.6) и, следовательно, к нарушению уровня полезности, если не увеличиться потребление сахара.

Анализ случая (3.2.7) предлагается читателю провести самостоятельно.

Как показывает пример 3.4 , функция (3.2.4) применяется для определения полезности набора взаимодополняющих друг друга товаров.

3. Неоклассическая функция полезности (функция Кобба-Дугласа):

где а - фактор шкалы измерения полезности,   . Для построения кривых безразличия функции (3.2.8) в   из уравнения  найдем

то есть карту безразличия составляет семейство (по параметру с) гипербол.

В приведенных примерах функции (3.2.3) и (3.2.8) заданы явным образом, а функция (3.2.4) находится как решение системы неравенств   .

Приведем без комментариев еще несколько видов функции полезности.

4. Функция полезности замещающе-дополняющего типа:

где функции   находятся из системы неравенств

5. Квадратичная функция полезности:

где   ,   -транспонированный вектор х, В - отрицательно определенная   -матрица.

6.Логарифмическая функция полезности (функция Бернулли)

:

где   .

7.Экспоненциальная функция полезности:

где   .

Читателю, в качестве упражнения, предлагается построить карты безразличия функций (3.2.9) - (3.2.12) в   .

Мы перечислили только некоторые из применяемых в теории потребления функций полезности. Список таких "готовых" функций можно продолжить. Однако здесь уместно повторить то, что говорилось ранее о математических моделях в целом - нельзя гарантировать пригодность известных функций для каждого конкретного случая. При моделировании задачи потребителя как раз самым уязвимым местом является функция полезности, адекватно отражающая предпочтения индивидуального потребителя. Поэтому часто требуется не выбрать, а построить для данной конкретной задачи свою функцию полезности. Один из методов приближенного построения функции полезности, использующей понятие предельной нормы замещения .

Наиболее общими для построения функций полезности являются методы регрессионного анализа , которые применимы при наличии подходящего статистического материала. Для выбранного вида функции полезности на основе этих данных оцениваются ее коэффициенты (параметры). Сложность метода зависит от класса функций (линейных, квадратичных, степенных и др.), в котором ищется функция полезности.

Принятие решения как составная часть процесса анализа информации.

Системный анализ является прикладной наукой, его конечная цель -изменение существующей ситуации в соответствии с поставленными целями. Окончательное суждение о правильности и полезности системного анализа можно сделать лишь на основании результатов его практического применения. Конечный результат будет зависеть не только от того, насколько совершенны и теоретически обоснованы методы, применяемые при проведении анализа, но и от того, насколько грамотно и качественно реализованы полученные рекомендации.