III. Методы раскрытия неопределенностей
При
решении заданий на вычисление предела
функции одной переменной встречаются
различные виды неопределенностей. А
именно: неопределенность вида
,
,
,
,
.
Различные виды неопределенностей имеют свои методы раскрытия.
3.1. Неопределенность вида
Разложение числителя и знаменателя на множители с последующим сокращением
Примеры:
1. Найти
Решение:
При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость
вида
.
Для раскрытия неопределённости разложим
числитель и знаменатель на множители,
и сократим дробь на общий множитель.
Для квадратного
трёхчлена
Где
Для 3x2+x-4
получим:
Для
получим:
Тогда
Ответ: -7
2. Найти
Решение:
При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида . Для раскрытия неопределённости разложим числитель и знаменатель на множители, и сократим дробь на общий множитель.
Для квадратного трёхчлена:
где
Для
получим:
Числитель разложим
на множители следующим образом:
Тогда
Ответ:
3. Найти
Решение:
При непосредственной подстановке предельного значения x=3 числитель и знаменатель обращаются в нуль
Имеем неопределённость вида . Для раскрытия неопределённости разложим числитель и знаменатель на множители, и сократим дробь на общий множитель.
Для квадратного трёхчлена
где
Для
получим:
Знаменатель разложим по формуле
Для
получим:
Тогда
Ответ:
Деление многочлена на многочлен
1. Найти
Решение:
=
=
-неопределенность,
для раскрытия требуется дробь сократить.
Т
ак
как x=1
– корень многочленов, то многочлены
кратны одночлену (x
– 1):
x³+x²-2x x-1 3x³-3 x-1
-(x³-x²)
x²+2x
-(3x³-3x²)
3x²+3x+3
2x²-2x 3x²-3
-(2x²-2x) -(3x²-3x)
0 3x-3
-(3x-3)
0
Разложим числитель и знаменатель на множители и сократим дробь:
Вычислим предел:
.
Ответ:
Устранение иррациональных разностей домножением на сопряженное выражение
Примеры:
1. Найти
Решение:
При непосредственной подстановке предельного значения x=0 числитель и знаменатель обращаются в нуль.
Имеем неопределённость
вида
.
Используя формулу
для раскрытия неопределённости домножим
числитель и знаменатель на сопряжённый
двучлен
,
А затем при наличии общего множителя сократим на него дробь.
Ответ:
2. Найти
Решение:
При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость
вида
.
Используя формулу
для раскрытия неопределённости домножим
числитель и знаменатель на сопряжённый
двучлен
и
,
а затем при наличии общего множителя
сократим на него дробь
Ответ:
3. Найти
Решение:
При непосредственной подстановке предельного значения x=0 числитель и знаменатель обращаются в нуль.
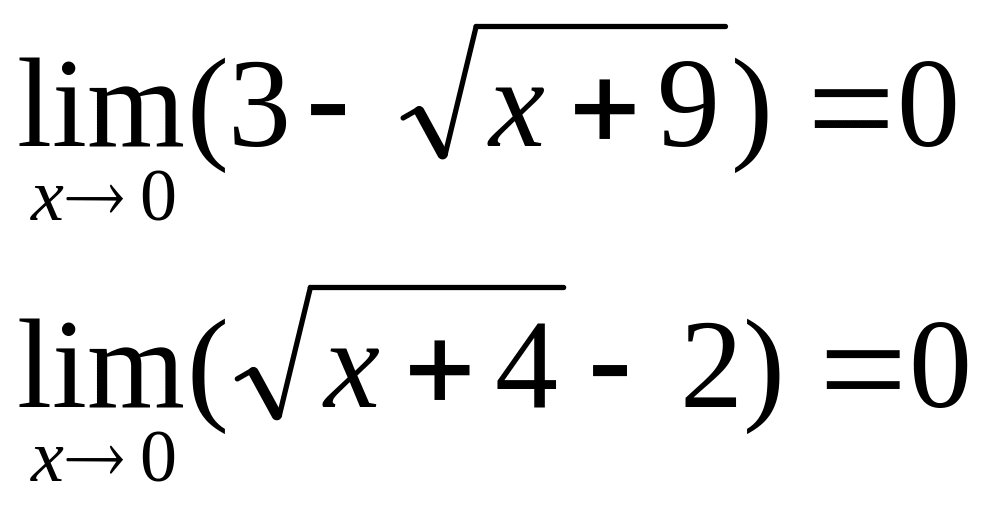
Имеем неопределённость
вида
.
Для раскрытия неопределённости домножим
числитель и знаменатель соответственно
на сопряжённые двучлены
и
,
а затем при наличии общего множителя
сократим на него дробь.
Ответ:
Замена переменной
Пример:
Найти
Решение:
При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость
вида
.
Для раскрытия неопределённости избавимся
от иррациональности сделав замену
(x=t3).
Тогда при
.
Затем после преобразований сократим дробь на общий множитель.
Ответ:
4
Первый замечательный предел
Примеры:
1. Найти
Решение:
При
числитель и знаменатель обращаются в
нуль.
Имеем неопределённость вида . Раскроем неопределённость с помощью 1-го замечательного предела после следующих преобразований:
Ответ:
2. Найти
Решение:
При числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида . Раскроем неопределённость с помощью 1-го замечательного предела после следующих преобразований:
Ответ:
3. Найти
Решение:
При числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида . Раскроем неопределённость с помощью 1-го замечательного предела после следующих преобразований:
Ответ:
Правило Лопиталя
Найти
Решение:
Ответ: 1