2. Практическое задание №2.

определение нормы годового стока на примере.

2.1. Вычисление характеристик годового стока. Задача. Вычислить характеристики годового стока реки Оби у г. Новосибирска.

Исходные данные:

1.Даны величины средних годовых расходов воды (см. табл.2.2)

2.Площадь бассейна реки до створа F=246000 км²

Требуется определить:

1 .Норму стока Q_N в разных размерностях – Q_N; M_N; W_N; h_N

2. Рассчитать среднюю квадратическую ошибку вычисления нормы стока воды _N

3. Рассчитать объем годового стока к конкретно выданной реке.

4. Рассчитать все необходимые величины для построения интегральной кривой стока конкретно по реке (пользуясь образцом табл.2.2)

Решение.

1. Суммируем все среднегодовые расходы реки за ряд лет: Q=112564 при периоде наблюдений n=64 года.

2. Определяем норму годового стока:

Q_N= = =1760

Норма стока в других размерностях равна:

а) в виде модуля стока М_N = 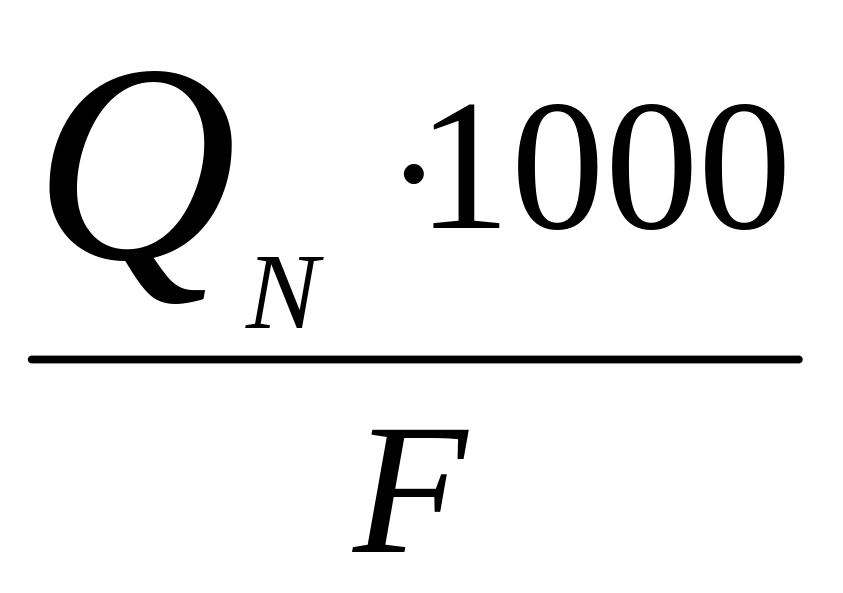= = 7,15 с 1 км²;

б) в виде объема стока W_N= Q_Nх31,536х10⁶= 1760х31,536х10⁶= 55503 млн. м³

в) в виде слоя стока h_N = 31,536хМ_N= 31,536х7,15= 225мм.

3. Средняя квадратическая ошибка нормы стока определяется при С_v = 0,20 по формуле % или в абсолютном выражении

Максимальная ошибка вычисления нормы годового стока допускается в 2,5-3 раза больше, т.е. = 2,5х3 = 7,5% или в абсолютном выражении х1760 = 0,075х1760 = 132 , т.е. наша ошибка 2,5% (или 44 ) гораздо ниже допустимой.

2.2. Построение интегральной кривой стока.

Задача. Построить интегральную кривую стока в косоугольных координатах.

4. Объем годового стока рассмотрим на примере реки Томи у г. Сталинска (см. табл.2.3). Пользуясь месячными расходами Q м³/сек, определяем объем стока за каждый месяц по формуле W=QTм³, где Т – число секунд в месяце.

Таблица 2.1.

Число дней в месяце	Число секунд в месяце	Число секунд в месяце, в млн.
28	2419200	2,42
29	2545600	2,54
30	2592000	2,59
31	2678400	2,68
Среднее	2629800	2,63

Следовательно, в графе 3 табл.2.3 получаем: W₁ =Q₁Т₁ = 115х2,68 = 308 млн.м³, где

Т₁ = число млн. сек в январе месяце,

W₂= … и т.д. Заполняем графу 3 табл.2.3.

5. Далее рассчитывается суммированный объем стока для графы 4 табл.2.3.

W₁ = 308 млн.м³; W₂ = 308+240=548 млн.м³ и т.д.

6. Далее рассчитываем средний месячный объем стока:

W_ср = = 2210 млн.м³

7. Затем суммируем значения среднего суммарного стока последовательно по месяцам и записываем в графу 5 табл.2.3.

W₁ = 2210; за 1 и 11 W_1-2 = 2210+2210 = 4420 млн.м³ и т.д.

8. Определяем разности W между суммарным фактическим стоком (графа 4) и суммарным равномерно распределенным стоком (графа 5), записывая полученные значения в шестую графу табл.2.3.

Например, W₁ = 308 – 2210 = - 1902 млн. м³, W₂ = 548 – 4420 = - 3872 млн. м² и т.д. до конца.

9. Строим интегральную кривую стока в косоугольных координатах.

ПОРЯДОК ПОСТРОЕНИЯ:

а). Сначала выбирается горизонтальный масштаб (времени) и вертикальный масштаб ( W) графика. В данном случае, горизонтальный масштаб назначаем 1 месяц – 1см. Масштаб вертикальной шкалы назначается исходя из крайних значений W, и для данного случая будет равен 1000 или 2000 млн. м³ в 1см.

б). Через нулевое значение W проводится горизонтальная линия ОО (нулевая линия отсчета разностей стока W).

в). Откладываем положительные и отрицательные значения W и, соединяя нанесенные точки, получаем интегральную кривую стока.

г). Для отсчетов объемов стока по интегральной кривой за любой месяц рассматриваемого периода строим косую сетку, проводя прямую через любую временную точку, например конец мая (точка Б) и соответствующее этому периоду значение объема стока =11050 млн. м³ из графы 5 (точка А). Получаем направление шкалы для отсчета объемов стока (пунктирная линия).

д). Проводя параллели линии АБ через точки, лежащие на вертикальной шкале W=4000, 8000, 12000 млн. м³ и т.д., получаем линии равных объемов суммарного стока.

е). Проверка построения косых линий производится по последней точке суммарного стока ′=53053 млн. м³, т.е. точке С на графике должна отвечать эта величина ′.

ж). Лучевой масштаб для определения средних расходов по интегральной кривой стока строится следующим образом:

Справа от графика проводим линию, перпендикулярную линии ОО, продолжая ее до пересечения с какой-либо косой линией шкалы объемов стока (с линией W=48000 млн. м³). Точка пересечения является началом лучевого масштаба расходов (нуль расходов). Масштаб расходов выбираем в зависимости от максимального среднего месячного расхода по таблице 2.3, равного, в данном случае, 4970 м³/сек (май 1941г.).

Принимаем для лучевого масштаба размерность: 1 см=200 м³/сек, и откладываем такие деления на шкале расходов вверх от точки нуля расходов.

з). Положение полюса лучевого масштаба Р определяется следующим образом: На масштабной шкале расходов откладываем средний месячный расход за весь период наблюдений Q_ср=853 м³/сек и, через полученную точку, проводим линию, параллельную линии ОО. Точка пересечения этой линии и вертикальной линии, проведенной через точку С (конец периода наблюдений), будет полюсом Р лучевого масштаба. Соединяя соответствующие расходы на масштабной шкале с полюсом Р, получаем лучевой масштаб для отсчета расходов по интегральной кривой стока.

10. Пользование интегральной кривой стока:

а). Определить суммарный сток реки за период с 1 января 1941г. по 9 мая 1942г. Проводим перпендикуляр от точки Т₁ (9 мая 1942г.) до пересечения с кривой стока в точке е; W= 34500 млн. м³.

б). Определить объем стока с 9 мая по 15 июня 1942г.

Проводим аналогичные перпендикуляры от точек Т₁ и Т₂ (15 июня). Значения стока устанавливаем по точкам пересечения с кривой стока e и f. Получаем W_e-f = 42000-34500= 7500 млн. м³.

в). Определить средний расход за этот период:

Q_ср= = = 2346 м³/сек.

Средние годовые расходы р. Оби у г. Новосибирска за 1894 - 1957 гг.

Таблица 2.2.

№№ п/п	Годы	Расходы воды Q м3/сек	№№ п/п	Годы	Расходы воды Q м3/сек
1	1894	1770	38	1931	1710
2	1895	1790	42	1935	1620
3	1896	1180	43	1936	2090
4	1897	1810	49	1942	2050
9	1902	1790	50	1943	1550
10	1903	2120	51	1944	1580
18	1911	1480	52	1945	1220
19	1912	1870	57	1950	2000
23	1916	1850	58	1951	1370
24	1917	1250	63	1956	1760
25	1918	1230	64	1957	1980
37	1930	2160		СУММА	112564

Примечание. Таблица дана в сокращенном виде.

Данные для построения интегральных кривых стока р. Томи

У г. Сталинска

Таблица 2.3.

Год и месяц	Средний месячный расход Q, м/сек3	Объем стока W млн.м3	Суммирование стока W млн.м3	Для построения кривой в косоугольных координатах
				При равномерном стоке W млн.м3	Разность стока W-W млн.м3
1941 I II III IV V VI VII VIII IX X XI XII 1942 I II III IV V VI VII VIII IX X XI XII	115 98.9 103 939 4970 2630 1210 347 258 349 185 119 90.8 71.3 69.8 649 2880 1660 777 581 339 854 558 206

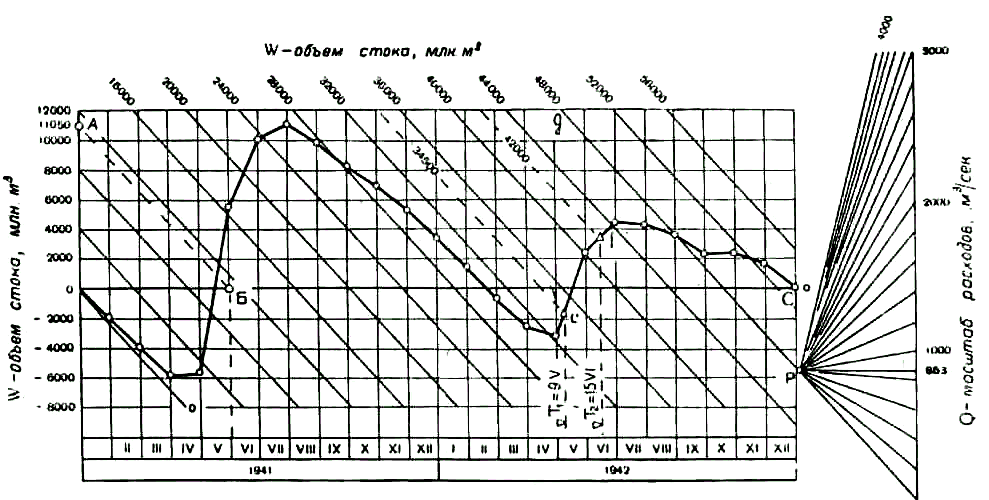
Рис. 2.1. Интегральная кривая годового стока р. Томи у г. Сталинска за 1941—1942 гг. в косоугольных координатах.