4. Задача № 3.

Вычисление и построение кривых обеспеченности максимальных раcходов дождевых паводков реки по короткому ряду и максимальному расходу редкой повторяемости.

1. Рассчитать обеспеченность (Р) кривой по фактическим максимальным расходам Q_maх.

2. Имея Q_maх и Р построить фактическую кривую обеспеченности (кружками)

3. Вычислить параметры Q_{ср. mах} и С_v кривой обеспеченности максимальных расходов при включении в непрерывный 16 – летний ряд наблюдений катастрофического максимума.

4. Рассчитать коэффициент асимметрии по формуле Крицкого и Менкеля.

5. По расчетным данным максимальных расходов Q_maх и обеспеченности Р построить теоретическую кривую обеспеченности (№ 1) с учетом катастрофического максимума.

6. Вычислить и построить теоретическую кривую обеспеченности (№ 2) максимальных расходов для короткого ряда (без учета катастрофического максимума)

7. Рассчитать гарантийную поправку.

8. Кривые строить на клетчатке Хазена.

Расчет средних расходов производится по формулам:

без учета Q_N:

с учетом Q_N: Q’_{ср. max} =

Расчет коэффициентов вариации производится по формулам:

без учета Q_N:

с учетом Q_N:

Расчет коэффициента асимметрии производится по формуле Крицкого-Менкеля:

Для построения теоретических кривых составляются две таблицы данных (см. табл. 4.1) с учетом и без учета катастрофического максимума.

Вычисление теоретической кривой обеспеченности средних годовых расходов воды при Q_ср=… м³/c, C_v=… и C_s=2C_v

Таблица 4.1.

p%	0,1	0,5	1	3	5	10	20	25	30	40	50	60	70	75	80	85	90	95	97	99
Ф или j
МS= Cv
КS= MS+1
Q= KSQcp м3/сек

Для построения клетчатки вероятностей Хазена используется таблица И. С. Рыбкина (см. табл. 4.1).

Таблица для построения клетчатки вероятностей (С.И. Рыбкина)

Таблица 4.1.

Значения абсциссы шкалы вероятностей P %	Горизон-тальное расстояние от средины (50%), мм	Значения абсциссы шкалы вероятностей P %	Горизон-тальное расстояние от средины (50%), мм	Значения абсциссы шкалы вероятностей P %	Горизон-тальное расстояние от средины (50%), мм
50	0	16	42,7	1,0	100,0
48	2,1	15	44,6	1,0	101,7
46	4,3	14	46,5	0,8	103,6
44	6,5	13	48,5	0,7	105,7
42	8,7	12	50,5	0,6	108,1
40	10,9	11	52,7	0,5	110,8
38	13,1	10	55,1	0,4	114,0
36	15,4	9	57,6	0,3	118,2
34	17,7	8	60,4	0,2	123,7
32	20,1	7	63,5	0,1	133,0
30	22,5	6	66,8	0,09	134,2
28	25,0	5	70,7	0,08	135,8
26	27,6	4,5	72,9	0,07	137,7
24	30,3	4,0	75,3	0,06	139,7
22	33,2	3,5	78,0	0,05	142,1
20	36,2	3,0	80,9	0,04	145,0
19	37,7	2,5	84,3	0,03	148,5
18	39,3	2,0	88,3	0,02	153,4
17	41,0	1,5	93,3	0,01	161,0

Данная клетчатка используется также для экстраполяции вычисленных кривых за пределы имеющихся наблюдений – до искомых малых и больших процентов обеспеченности, что очень ценно при расчетах для проектирования заданных характеристик гидросооружений и других водопользователей. Порядок построения на данной клетчатке и расчеты те же самые, что и для построения кривой обеспеченности в простых координатах.

Теоретическая кривая на чертеже проводится сплошной линией. Эмпирическая кривая строится на том же чертеже в виде отдельных точек или кружков (см. рис. 4.1).

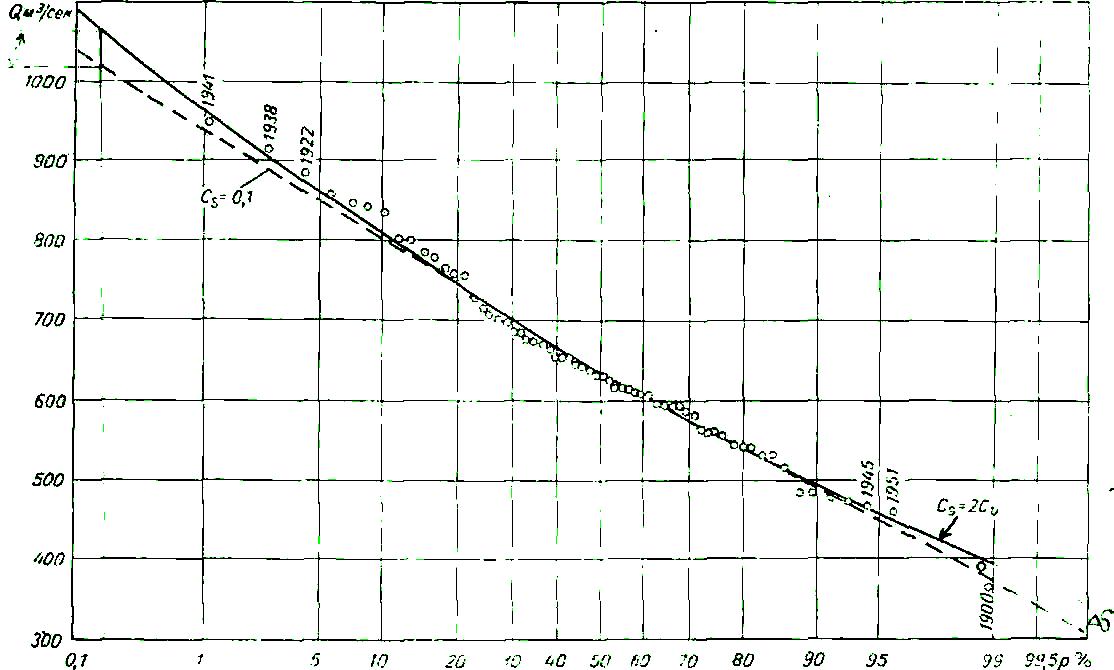
Рис. 4.1. Кривая обеспеченности средних годовых расходов воды в клетчатке вероятностей.

Расчет гарантийной поправки производится по формулам:

Q_max.р = или = х 100% ,

где Q_max.p – максимальный расход заданной обеспеченности;

- гарантийная поправка.

E_p – относительная средняя квадратичная ошибка расхода Q_max.p при n = 1, характеризующая степень изменчивости максимумов и определяемая по графику (рис.4.2) в зависимости от расчетной обеспеченности Р% и коэффициента вариации C_v; а – коэффициент, характеризующий гидрологическую изученность реки равный:

• 1,5 для слабоизученных в гидрологическом отношении территорий;

• 0,8 для хорошо изученных территорий.

Гарантийная поправка принимается не более 20% максимального расхода воды Q_{max.p .} Тогда исправленный расход определяется по формуле

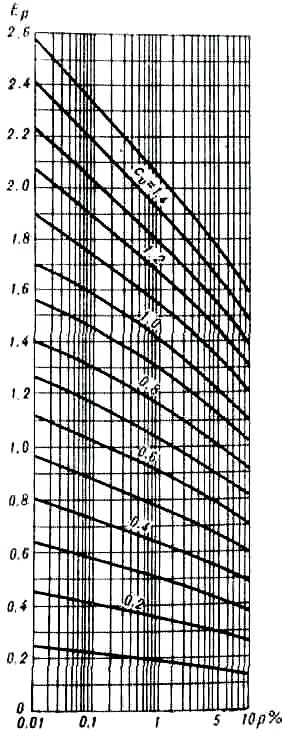
Рис. 4.2. График величины Ер для определения DQ_max.