45. Формальные грамматики и языки. Синтаксические деревья. Задачи разбора и вывода.

Язык - подмножество цепочек слов некоторого алфавита.

Алфавит - непустое конечное множество элементов (символов).

Цепочка - всякая конечная последовательность символов. Например, пусть А = {а,b,с} - алфавит, тогда "а", "b", "с" - символы этого алфавита, а "а", "b", "с", "аа", "аb", "ас", "bа" и т.д. - цепочки символов этого алфавита.

Продукция (правило постановки) - это упорядоченная пара (U, х), записываемая как U  х, где U - символ, а х - цепочка (конечная).

Грамматикой G называется совокупность G = (N, T, Р, S),

где N - множество нетерминальных символов алфавита;

T - множество терминальных символов алфавита;

Р - множество правил продукции;

S - начальный символ грамматики.

При этом N ∩ T = , N  T = алфавит, S  N - начальный символ грамматики, принадлежащий множеству нетерминальных символов, и P={U  x} (UN, xNT).

сентенциальная форма (СФ) - это любой промежуточный или конечный результат вывода из S - начального символа грамматики G.

Если х - СФ в грамматике G и х состоит только из терминальных символов, то цепочка х - это предложение в грамматике G.

Языком в грамматике G называется множество возможных предложений в G: L(G) = {х | S ^* х, x  T⁺}.

Пусть G - грамматика, а w = хuу - СФ. Тогда u называется фразой СФ w для нетерминального символа U, если S ^* хUу и U ⁺ u; и простой фразой, если S ^* хUу и U = u.

Основой всякой СФ называется самая левая простая фраза.

Каждая грамматика описывает (задает) некоторый язык, и каждый язык описывается (задается, порождается) некоторой грамматикой.

Синтаксические деревья. Задачи разбора и вывода

Задачи анализа текстов на тех или иных языках достаточно наглядно демонстрируются с помощью синтаксических деревьев. При определении синтаксического дерева (СД) используют следующие понятия:

дерево - это множество узлов и связей (ветвей) - такое, что в любой узел (кроме одного) входит лишь одна связь (ветвь);

корневой узел - это единственный узел дерева, не имеющий вводящей ветви;

куст узла - это множество узлов, непосредственно связанных с данным узлом ветвями (множество подчиненных узлов);

концевые узлы - это узлы с пустыми кустами (листья дерева);

поддерево - это любой некорневой узел со своим кустом (рассматриваемое отдельно от полного дерева, поддерево становится деревом).

Для иллюстрации введенных понятий и их отношения к теории формальных грамматик целесообразно привести следующий пример. Пусть имеется грамматика G:

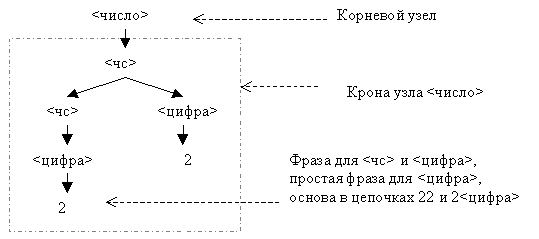
G = ({<число>,<чс>,<цифра>},{0,1,...,9},Р,<число>),

где Р = {<число>  <чс>, <чс>  <чс> <цифра>, <чс>  <цифра>, <цифра>  0 | 1 | 2 | ... | 9}.

На рис изображено СД для предложения 22, записанного в грамматике G.

Правила построения СД для произвольного предложения в некоторой грамматике весьма просты:

1. в качестве корневого узла строится узел S (где S - начальный символ грамматики);

2. в имеющемся дереве выбирается узел U, для которого в Р имеется продукция U  α₁ ... α_k (если такого узла нет, то построение завершено);

3. к дереву добавляются узлы α₁, ..., α_k и связи (U,α₁), …, (U,α_k), и процесс повторяется, начиная с п. 2.

процесс построения должен завершиться или иметь возможность завершиться в таком состоянии, когда все концевые узлы связаны с терминальными символами. При этом просмотр концевых узлов слева направо дает предложение грамматики, а концевые узлы в любой момент построения дерева образуют СФ.

Для успешного осуществления процесса компиляции необходимо: ответить на вопрос "принадлежит ли текст программы входному языку?", т.е. является ли исходная программа совокупностью предложений входного языка;определить синтаксическую структуру программы.

Очевидно, что решение этих задач требует построения СД. Сам факт построения такого дерева будет свидетельствовать о том, что исходная программа является синтаксически правильной (с позиций грамматики входного языка), а СД позволит сформировать объектный код.

Подстерегающая здесь опасность - возможная неоднозначность процесса вывода.Например, пусть имеется грамматика G = ({а}, {+, , (, ), i}, {а  а+а | аа | (а) | i}, а). На рис. 1.5 показаны два синтаксических дерева, соответствующие выводу цепочки i+ii. Такая ситуация может привести к совершенно разным трактовкам смысла цепочки.

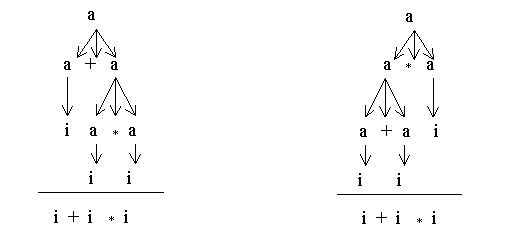
Грамматики, в которых хотя бы одно предложение имеет более одного порождающего дерева, называется неоднозначными.

Практически используют две стратегии вывода:

левый вывод – на каждом шаге вывода производится развертывание самого левого концевого узла (допускающего это);

правый вывод - осуществляется путем замены самого правого концевого узла, не соответствующего терминальному символу, правой частью одного из правил.