Тема 1.5 Задачи транспортного типа

Задача 63. Имеется два поставщика однородного груза, запасы которого составляют 100 и 250 тонн соответственно. Этот груз нужно доставить трём потребителям с потребностями соответственно 90; 80 и 180 тонн. Стоимость перевозки 1 тонны груза от каждого поставщика каждому потребителю задана матрицей тарифов:

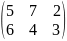
Составить план перевозок, для которого суммарная стоимость всех поставок будет наименьшей.

Задача 64. Имеются поставщики А1, А2, и А3 с запасами груза соответственно 200; 250 и 50 тонн. Этот груз необходимо доставить потребителям В1, В2, В3, В4 и В5 в количествах соответственно 100: 70; 80; 150 и 100 тонн. Стоимость перевозки 1 тонны груза от каждого поставщика каждому потребителю задана матрицей тарифов:

7 5 2 3 4

6 4 5 2 7

5 8 3 5 9

Составить план перевозок, для которого суммарная стоимость всех поставок будет наименьшей.

Задача 65. В трёх пунктах производится некоторый продукт в количествах 118;

Задача 66. В трёх пунктах производится некоторый продукт в количествах 118; 18 и 98 ед. соответственно. Произведённый продукт нужно отправить автомобильным транспортом в пять пунктов, заявки от которых составляют 68; 68; 90; 31 и 87 ед. Известна матрица расстояний (в км.) от каждого производителя каждому потребителю:

Требуется найти план перевозок продукции, при котором суммарные транспортные расходы будут минимальными.

Задача 67. Имеются механизмы четырёх типов, которые нужно распределить между тремя участками А, В и С. Количество механизмов каждого типа составляет соответственно 74; 53; 45 и 24 ед. Известны потребности в механизмах для каждого участка: 90; 61 и 45 ед. соответственно. Производительность механизма каждого типа на каждом участке работ (объём работы /ед. времени), задана матрицей:

Требуется найти такое распределение механизмов между участками, при котором их суммарная производительность будет наибольшей.

Задача 68. Для рациональной организации производства, четырёх сотрудников Иванова, Петрова, Сидорова и Егорова нужно назначить на четыре рабочих места:1; 2; 3 и 4. Величина месячной прибыли в тыс. руб., которую каждый сотрудник может обеспечить на каждом рабочем месте, задана матрицей оценок:

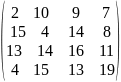
Назначить всех сотрудников на рабочие места так, чтобы суммарная прибыль была максимальной.

Задача 69. Решить задачу о коммивояжёре для четырёх городов , расстояния между которыми заданы матрицей расстояний:

0 2 1 3

2 0 8 7

1 8 0 6

3 7 6 0 .

Решить задачу комбинаторным методом.

Задача 70. Имеются пять населённых пунктов, расстояния между которыми известны и заданы матрицей D:

а) 0 7 2 9 7

5 0 3 9 1

D = 4 8 0 5 3

5 6 4 0 7

7 6 3 7 0

в) 0 3 6 1 4

9 0 9 3 8

D = 7 1 0 7 5

1 4 6 0 1

2 5 1 8 0 .

Найти самый короткий маршрут, при котором все города будут посещены только один раз и коммивояжёр возвратится в исходный город. Воспользуйтесь методом ветвей и границ.