4. Пусть f: {1,2,3}  {1,2,3}, g: {1,2,3}  {1,2,3}, h: {1,2,3}  {1,2,3} – отображения, показанные на рисунке:

1. gf g

2. hgf

3. hf g

4. gh g

5. hf h

6. fgf

7. gf h

8. hgh

9. f hf

10. gh f

1. А = ;

2. А = ;

3. А = ;

4. А = ;

5. А= ;

6. А= ;

7. А= ;

8. А = ;

9. А= ;

10. А= ;

1. В={xN | x41,

x–квадрат числа}

A={xR | (x² + x +1)(x²–x–6)=0}

2. В={xN | x – делитель 40}

A={xR | (x² – x –2)(x²–x–20)=0}

3. В={xN | x – делитель 81}

A={xR |(x²+x –2)(x²–7x +6)=0}

4. В={xN |x51,

x–квадрат числа}

A={xR |(x²–3x–4)(x²–9x+20)=0}

5. В={xN |x65,

x–квадрат числа}

A={xR |(x²–6x+5)(x²–x–12)= 0}

6. В={xN | x – делитель 54}

A={xR |(x²–5x–6)(x²–5x+4) = 0}

7. В={xN | x – делитель 36}

A={xR |(x²+3x–4)(x²+x–12)=0}

8. В={xN |x64,

x–квадрат числа}

A={xR|(x²+4x–5)(x²–7x+12)= 0}

9. В={xN |x78,

x–квадрат числа}

A={xR |(x²–3x+2)(x²–4x–5)= 0}

10. В={xN | x – делитель 32}

A={xR | (x²–5x+6)(x²+x–20)= 0}

А

Сколько существует подмножеств у конечного множества? Почему?

Б

Какими свойствами обладает операция пересечения множеств?

В

Что понимается под “элемент”, “множество”, “подмножество”?

Г

Какими свойствами обладает операция объединения множеств?

Д

Как проиллюстрировать диаграммами Венна дистрибутивные законы?

Е

Что такое мощность множества?

Ё

Какие множества имеют несчетную мощность?

Ж

Какие множества имеют счетную мощность?

З

Какими свойствами обладает операция пересечения множеств?

И

Какими свойствами обладает универсальное множество?

Й

Какие множества эквивалентны множеству натуральных чисел?

К

Как проиллюстрировать диаграммами Венна законы поглощения?

Л

Как формулируются законы Де Моргана над множествами?

М

Какие множества называются несобственными?

Н

Какими свойствами обладает операция разности множеств?

О

Как доказать эквивалентность двух множеств?

П

Какие способы задания множеств вы знаете?

Р

Какими свойствами обладает пустое множество?

С

Какие операции выполняются над множествами?

Т

Как проиллюстрировать диаграммами Венна законы ДЕ Моргана?

У

Какие множества называются равными?

Ф

Какими свойствами обладает операция симметрической разности?

Х

Какие множества называют равными?

Ц

Как проиллюстрировать диаграммами Венна коммутативные законы?

Ч

Какими свойствами обладает операция дополнения до универсума?

Ш

Как формулируются законы поглощения теории множеств?

Щ

В чем отличие понятий “принадлежность множеству” и “включение в множество”?

Ъ

Как проиллюстрировать диаграммами Венна ассоциативные законы?

Ы

Какие Вам известны виды отображений множеств?

Ь

Какие множества называют эквивалентными?

Э

Какими свойствами обладает операция объединения множеств?

Ю

Какие отношения множеств Вам известны?

Я

Какие множества называют конечными, бесконечными?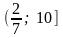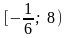