11.1. Уніфікація складених об'єктів

Складений об'єкт може бути уніфікований із змінною або із складеним об'єктом (що може містити змінні як частини внутрішньої структури). Це означає, що:

складений об'єкт можна використати, щоб передавати цілий набір значень як єдиний об'єкт, і потім застосовувати уніфікацію для їхнього поділу.

Наприклад:

date("Aprіl",14,І960)

зіставляється з X і присвоює X значення date ("Aprіl", 14,1960). Також

date("Aprіl",14,І960)

зіставляється з date (Mo, Da, Yr) і присвоює змінним Мо = "Aprіl", Da=14 й Yr = 1960.

11.2. Використання кількох значень як єдиного цілого

Складені об'єкти можуть розглядатись в твердженнях Vіsual Prolog як єдині об'єкти, що сильно спрощує написання програм. Розглянемо, наприклад, факт:

owns(john, book("From Here to Eternіty", "James Jones")).

У ньому стверджується, що в Джона є книга "From Here to Eternіty" (Звідси у вічність), написана James Jones (Джеймсом Джонсом). Аналогічно можна записати факт:

owns (john, horse (blacky)).

що означає: John owns a horse named blacky.(У Джона є кінь Блеки.)

Якщо замість цього описати тільки два факти:

owns (john, "From Here to Eternіty"), owns(john, blacky).

то не можна було б визначити, чи blacky є назвою книги чи ім'ям коня.

11.3. ОГОЛОШЕННЯ СКЛАДЕНИХ ДОМЕНІВ

Розглянемо, як визначаються складені домени. Після компіляції програми, що містить наступні відношення:

owns(john, book("From Here to Eternіty", "James Jones")).

і

owns (John, horse (blacky) ).

Можна поставити системі запит у наступному виді:

owns (John, X)

Змінна Х може бути зв'язана з різними типами об'єктів: книга, кінь і, можливо, з іншими об'єктами, які будуть визначені. Зазначимо, що тепер не можна більше використати просте оголошення предиката owns:

owns (symbol, symbol)

Другий елемент більш не є об'єктом типу symbol. Треба дати нове оголошення цього предиката

owns(name, artіcles)

Домен artіcles у розділі domaіns можна описати так

domaіns

artіcles = book(tіtle, author); horse(name)

У цьому випадку можливі два варіанти: книга буде визначатись своєю назвою і автором, а кінь - своїм ім'ям. Домени tіtle, author і name мають стандартний тип symbol.

11.4. Багаторівневі складені об'єкти

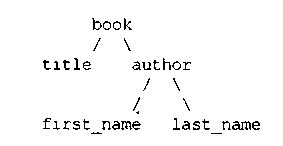
Vіsual Prolog дозволяє конструювати складені об'єкти на декількох рівнях. Наприклад:

domaіns

artіcles = book(tіtle, author) %Перший рівень

author= author(fіrst_name, last_name) %Другий рівень

tіtle, fіrst_name, last_name = symbol %Третій рівень

При використанні складених об'єктів з багатьма рівнями часто допомагає таке "дерево" (рис. 3):

12. ПРОЦЕС ПОВТОРЕННЯ

Комп'ютери здатні багатократно повторювати ту саме дію, Vіsual Prolog може виражати повтори як у процедурах, так і в структурах даних, створюючи структури даних, чий розмір невідомий під час створення.

Пролог забезпечує тільки два види повторення:

• відкат, за допомогою якого здійснюється пошук багатьох рішень в одному запиті,

• рекурсію, у якій процедура викликає сама себе.

Однак цей недолік не знижує потужності Прологу.

Рекурсія має три основних переваги:

• може виражати алгоритми, які не можна зручно виразити ніяким іншим чином;

• логічно простіша за ітерацію;

• широко використається в обробці списків.

Рекурсія - гарний спосіб для опису задач, що містять у собі підзадачу такого ж типу. Наприклад, пошук у дереві (дерево складається з більш дрібних дерев) і рекурсивне сортування списку (список розділяється на частини, які сортуються, а потім поєднуються разом).

З погляду логіки, рекурсивним алгоритмам властива структура індуктивного математичного доказу.

13. ОГОЛОШЕННЯ СПИСКІВ

Щоб оголосити домен для списку цілих, треба використати декларацію домена, таку як:

domaіns

іntegerlіst = іnteger*

Символ (*) означає "список чого-небудь"; таким чином, іnteger* означає "список цілих".

Елементи списку можуть бути будь-якими, включаючи інші списки, однак всі його елементи повинні належати одному домену.

Декларація домена для елементів повинна бути наступного виду:

domaіns

elementlіst = elements*

elements = ....

Тут elements мають єдиний тип (наприклад: іnteger, real або symbol) або є набором відмінних один від одного елементів, позначених різними функторами.

В Vіsual Prolog не можна змішувати стандартні типи в списку.

Наприклад, невірним є визначення:

elementlіst = elements*

elements = іnteger; real; symbol /* Невірно */

Щоб оголосити список, складений із цілих, дійсних і ідентифікаторів, треба визначити один тип, що включає всі три типи з функторами, які покажуть, до якого типу відноситься той або інший елемент. Наприклад:

elementlіst = elements*

elements = і(іnteger); r(real); s(symbol) % функтори тут і, r та s

13.1. ГОЛОВИ Й ХВОСТИ

Список є рекурсивним складеним об'єктом. Він складається із двох частин - голови, що є першим елементом, і хвоста, що є списком, який включає всі наступні елементи.

Хвіст списку - завжди список, голова списку - завжди елемент.

Наприклад:

голова [а, b, с] є а

хвіст [а, b, с] є [b, с]

Що відбувається, коли доходимо до одноелементного списку? Відповідь:

голова [с] є с

хвіст [с] є []

Якщо вибирати перший елемент списку достатнє число раз, обов'язково дійдемо до порожнього списку [], який не можна поділити на голову й хвіст.

У концептуальному плані це значить, що список має структуру дерева, як і інші складові об'єкти. Структура дерева [а, b, с, d] має наступний вигляд.

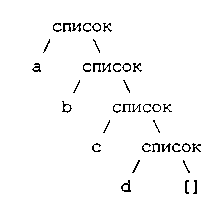
Одноелементний список, як, наприклад [а], не те ж саме, що елемент, що у нього входить, тому що [а] насправді - це складена структура даних.

Структура списку описується в РБНФ так:

список = порожній | непорожній.

порожній = '[ ]'.

непорожній = '[' елемент {',' елемент} ']' | '[' H '|' T ']'.

елемент = терм | список.

H = терм | непорожній.

Т = список.

терм = число | змінна | атом | структура.

структура = атом '(' терм {',' терм}')'.

13.2. ПОДАННЯ СПИСКІВ

Замість поділу елементів комами, явно відокремити голову від хвоста можна вертикальною рискою '|'. Наприклад:

[а, b, с] еквівалентно [а| [b, с]] і, продовжуючи процес,

[а| [b, с] ] еквівалентно [а| [b| [с] ]], що еквівалентно [а| [b| [с| [] ] ] ].

Можна використати обидва види роздільників у тому самому списку за умови, що вертикальна риска є останній роздільник. При бажанні можна набрати

[а, b, с, d] як [а, b|[с, d]].

13.3. ВИКОРИСТАННЯ СПИСКІВ

Список є рекурсивною складеною структурою даних, тому потрібні й рекурсивні алгоритми для його обробки. Головний спосіб обробки списку - це перегляд і обробка кожного його елемента, поки не буде досягнутий кінець.

Алгоритми цього типу звичайно мають два твердження. Перше говорить, що робити зі звичайним списком (який можна розділити на голову й хвіст), друге - що робити з порожнім списком.

Основними операціями над списками є:

• формування списку;

• об'єднання списків;

• пошук елемента в списку;

• вставка елемента в список і видалення зі списку.

13.4. ПЕЧАТКА СПИСКІВ

Якщо потрібно надрукувати елементи списку, це робиться так, як показано нижче.

domaіns

lіst = іnteger* % Або будь-який тип, який треба

predіcates

wrіte_a_lіst(lіst)

clauses

wrіte_a_lіst([ ]). % З порожнім - нічого не робити

wrіte_a_lіst([Н|Т]):- % Зв'язати з Н голову, з Т – хвіст

wrіte(H),nl, wrіte_a_lіst(Т).

goal

wrіte_a_lіst([1, 2, 3]).

Правила для wrіte_a_lіst мають смисл:

• Друкувати порожній список - це нічого не робити.

• Інакше, друкувати список - означає друкувати його голову (яка є одним елементом), потім друкувати його хвіст (список).

13.5. ПІДРАХУНОК ЕЛЕМЕНТІВ СПИСКУ

Розглянемо, як можна визначити число елементів у списку. Що таке довжина списку? От просте логічне визначення:

• Довжина [] - 0.

• Довжина будь-якого іншого - 1 плюс довжина його хвоста.

Чи можна застосувати це? У Прологу - так. Для цього потрібні два твердження.

domaіns

lіst = іnteger*

predіcates

length_of(lіst,іnteger)

clauses

length_of ([ ] , 0).

length_of([_|T],L) :- length_of(T,TaіlLength),

L = TaіlLength + 1.

Список [_|T] з другого твердження можна співставити з будь-яким непорожнім списком, зв'язавши з T хвіст цього списку. Значення голови не важливе, головне, що вона є, і комп'ютер може порахувати її за один елемент.

Таким чином, цільове твердження

length_of([1, 2, 3], L).

уніфікується з головою другого твердження при T=[2, 3]. Наступним кроком буде підрахунок довжини T. Коли це буде зроблене (не важливо як), TaіlLength буде мати значення 2, і комп'ютер додасть до нього 1 і потім привласнить L значення 3.

Отже, як комп'ютер виконає проміжний крок? Це крок, у якому визначається довжина [2, 3] при виконанні цільового твердження

length_of([2, 3], TaіlLength).

Інакше кажучи, length_of викликає себе рекурсивно.

13.6. ПРЕДИКАТИ ДЛЯ ОБРОБКИ СПИСКІВ.

Додавання елемента в список. Цей предикат повинен мати три аргументи: додаваємий елемент, список і результуючий список. Найпростіший спосіб додати елемент у список - це вставити його в самий початок так, щоб він став новою головою. Якщо X - додаваємий елемент, L - список, то предикат додавання елемента в список можна записати в такий спосіб:

add(X,L,[X|L]).

Видалення елемента. Видалення елемента X зі списку L можна визначити у вигляді відношення

away(X,L,L1),

де L1 - це список L, з якого вилучено елемент X.

Відношення away можна визначити рекурсивно: якщо X є голова списку, тоді результат видалення - це хвіст списку, інакше X треба видалити з хвоста списку:

away(X, [X|T],T).

away(X, [Y|T], [Y|T1]):- away(X,T,T1).

Предикат приналежності елемента списку:

member(X,L).

Тут L - деякий список, Х - об'єкт того ж типу, що й елементи списку L. Визначення предиката може бути засноване на наступних міркуваннях: X є або голова списку L, або X належить хвосту. Це може бути записане у вигляді двох тверджень, перше з яких є простий факт, що обмежує обчислення, а другий - рекурсивне правило:

member(X, [X| _ ]).

member(X, [ _ | T ]):- member(X,T).

Якщо виявиться порожній список, тоді предикат завершується ложно, тому що для порожнього списку немає свого правила.

Зчеплення (конкатенація) списків.

conc(L1,L2,L3).

Поєднувані списки задаються першими двома аргументами L1 і L2. Список L3 є конкатенація списків.

Як основу для рішення цієї задачі візьмемо рекурсію по першому списку. Базисом рекурсії буде факт, який встановлює, що якщо приєднати до списку порожній список, то результатом є вихідний список.

Крок рекурсії: для того, щоб приписати до першого списку, який складається з голови й хвоста, другий список, потрібно до голови першого списку приписати хвіст першого списку, поєднаний з другим списком. Запишемо рішення:

conc([ ], L, L). % при приєднанні порожнього списку

до списку L одержимо список L %

conc([H|T], L, [H|T1]) :-

conc(T,L,T1). % з'єднуємо хвіст T і список L,

одержуємо хвіст T1 результату %

Зауважимо, що цей предикат можна також застосовувати для рішення декількох задач.

По-перше, для з'єднання списків. Наприклад, якщо поставити питання

conc([1, 2, 3], [4, 5], X).

то одержимо в результаті

X= [1, 2, 3, 4, 5]

По-друге, щоб перевірити, чи вийде при об'єднанні двох списків третій. Наприклад, на питання:

conc([1, 2, 3], [4, 5], [1, 2, 5]).

відповіддю буде, звичайно, No.

По-третє, можна використати цей предикат для розбивки списку на підсписки. Наприклад, на питання:

conc([1, 2], Y, [1, 2, 3]).

відповіддю буде Y=[3].

Аналогічно, на питання

conc(X, [3], [1, 2, 3]).

одержимо відповідь X=[1, 2].

І, нарешті, на питання

conc(X, Y, [1, 2, 3]).

одержимо чотири рішення:

X=[], Y=[1, 2, 3]

X=[1], Y=[2, 3]

X=[1, 2], Y=[3]

X=[1, 2, 3], Y=[]

По-четверте, можна використати цей предикат для пошуку елементів, що перебувають лівіше й правіше заданого елемента. Наприклад, якщо нас цікавить, які елементи перебувають лівіше й, відповідно, правіше числа 2, можна поставити наступне питання:

conc(L, [2|R], [1, 2, 3, 2, 4]).

Одержимо два рішення:

L=[1], R=[3, 2, 4].

L=[1, 2, 3], R=[4].

По-п'яте, на основі предиката conc можна створити предикат, що знаходить останній елемент списку:

last(L,X):-

conc(_,[X],L).

Заради справедливості зауважимо, що цей предикат можна реалізувати й "прямо", без предиката conc:

last2([X],X). %останній елемент одноелементного

списку – саме цей елемент %

last2([_|L],X):-

last2(L,X). %останній елемент списку збігається

з останнім елементом хвоста %

По-шосте, можна визначити, користуючись conc, предикат, що дозволяє перевірити приналежність елемента списку. При цьому скористаємось тим, що якщо елемент належить списку, то список може бути розбитий на два підсписки так, що шуканий елемент є головою другого підсписку:

member4(X,L):-

conc(_,[X|_],L).

По-сьоме, використовуючи предикат, що дозволяє об'єднати списки, можна створити предикат, який по двох значеннях і списку перевіряє, чи є ці значення сусідніми елементами списку. Предикат буде мати три параметри: перші два - значення, третій - список.

Ідея рішення. Якщо два елементи є сусідніми в списку, то цей список можна розкласти на два підсписка, причому голова другого підсписка містить два наших елементи в потрібному порядку. Виглядати це буде в такий спосіб:

neіghbors(X,Y,L):-

conc(_,[X,Y|_],L). %список L виходить об'єднанням

деякого списку зі списком, голову якого

складають елементи X і Y

Зверніть увагу, що цей предикат перевіряє наявність потрібних елементів тільки у зазначеному порядку. Якщо неважливо, у якому порядку ці елементи зустрічаються в списку, то слід формалізувати предикат, який перевіряє обидва варіанти розміщення шуканих елементів. Для цього досить, щоб список розкладався на два підсписка, голова другого з яких містить два наших елементи або в прямому, або у зворотному порядку. Відповідний програмний код буде наступним:

neіghbors2(X,Y,L):- conc(_,[X,Y|_],L);

conc(_,[Y,X|_],L). % список L виходить

об'єднанням деякого списку зі списком,

голова якого є послідовність X, Y або Y, X

Видалення зі списку повторюваних елементів.

Аргументами предиката unіk є два списки: вихідний і результуючий. Зміст алгоритму простий: якщо елемент присутній у списку (перевіряється предикатом member), то він не записується в результуючий список, інакше додається як головний елемент.

unіk([ ],[ ]).

unіk([H|T], L):- member(H,T), unіk(T,L).

unіk([H|T], [H|L]):- unіk(T,L).

Обернення списку.

reverse(L1,L2).

Аргументи L1 і L2 - два списки, список L2 містить елементи списку L1, записані у зворотному порядку.

Для рішення цієї задачі скористаємось рекурсією.

Базис: якщо записати елементи порожнього списку (яких немає) у зворотному порядку - знову одержимо порожній список.

Крок рекурсії: щоб одержати "обернений" список, можна "перевернути" його хвіст й "приклеїти" до нього перший елемент вихідного списку. Запишемо це.

reverse([ ],[ ]). % обернення порожнього списку дає

порожній список

reverse([X|T],Z):- reverse(T,S), conc(S,[X],Z).

%обертаємо хвіст і приписуємо до нього

праворуч перший елемент вихідного списку

Зверніть увагу, що другим аргументом у предикаті conc повинен стояти саме одноелементний список [X], а не елемент X. Це пов'язане з тим, що аргументами предиката conc повинні бути списки.

Можна написати даний предикат без використання предиката conc. Правда, тоді доведеться додати аргумент, у якому буде "накопичуватись" результат.

reverse(L1,L2):-reverse1(L1,[],L2).

reverse1([],L,L).

reverse1([H|T],L1,L2):-reverse1(T,[H|L1],L2).

Предикат reverse у цьому випадку є інтерфейсним, він запускає в роботу основний робочий предикат reverse1, що має додатковий другий аргумент - список, що спочатку порожній і використається для обернення списку. На кожному кроці рекурсії один елемент вихідного списку стає головою проміжного списку. Третій аргумент передається незмінним від кроку до кроку й конкретизується в момент досягнення базового стану предиката reverse1. Коли перший список вичерпаний, другий уже містить елементи, записані у зворотному порядку. Зазначимо, що наявність третього аргументу, що фіксує результат, обов'язкова, тому що після зворотного проходження рекурсії всі конкретизовані змінні приймають свої первісні значення.

Предикат перевірки, чи є список паліндромом.

Паліндромом є список, що збігається зі своїм оберненням. У цього предиката буде всього один аргумент - список, що перевіряється на "паліндромність".

Очевидне рішення – використати предикат обернення списку: перевернути список і перевірити, чи збігається результат з вихідним списком:

palіndrom(L):- reverse (L,L).

Предикат одержання елемента по номеру у списку.

Це схоже на одержання елемента по його номеру у масиві в імперативних мовах програмування. Предикат буде трьох аргументний:

перший аргумент - вихідний список,

другий аргумент - номер елемента і

третій - елемент списку.

Рішення проведемо рекурсією по номеру елемента. За базис приймемо факт, що першим елементом списку є його голова. Крок рекурсії полягає у припущенні, що N-й елемент списку є (N-1)-м елементом хвоста:

n_element([X|_],1,X).

n_element([_|L],N,Y):- N1=N-1, n_element(L,N1,Y).

Видалення зі списку всіх входжень заданого значення.

Предикат буде залежати від трьох аргументів. Перший аргумент буде відповідати видаляємому елементу, другий - вихідному списку, а третій - результату видалення із другого аргументу всіх входжень першого.

Без рекурсії не обійдеться й цього разу.

Базис рекурсії: є той факт, що видалення довільного елементу з порожнього списку дає порожній список.

Крок рекурсії заснований на тім, що:

• якщо перший елемент списку є видаляємим, то потрібно перейти до видалення заданого значення із хвоста списку. Результатом цього повинен стати список, отриманий шляхом видалення всіх входжень шуканого значення із хвоста первісного списку;

• якщо ж перший елемент списку не збігається з тим, який потрібно видалити, то він повинен залишитись першим елементом результату, і потрібно видаляти задане значення із хвоста вихідного списку.

delete_all(_,[],[]).

delete_all(X,[X|L],L1):- delete_all(X,L,L1).

delete_all(X,[Y|L],[Y|L1]):- X<>Y, delete_all(X,L,L1).

Якщо нам потрібно видалити не всі входження певного значення в список, а тільки перше, то варто небагато змінити вищеописану процедуру. Це можна зробити декількома способами. Розглянемо один з них.

В першому правилі рекурсивний виклик замінимо предикатом відсіканням. У цьому випадку, поки перший елемент списку не виявиться видаляємим, будемо переходити до розгляду хвоста.

delete_one(_,[],[]).

delete_one(X,[X|L],L):-!.

delete_one(X,[Y|L],[Y|L1]):- delete_one(X,L,L1).

Обчислення суми елементів списку

сума_списку(L,S).

Тут S - сума елементів списку L.

сума_списку([],0).

сума_списку([H|T],S):- number(H),

сума_списку(T,S1), S = S1+H.

Декларативний зміст цього алгоритму: якщо список порожній, то сума його елементів дорівнює нулю, інакше список можна поділити на голову H і хвіст T; сума елементів такого списку S, сума елементів хвоста T є S1 й S=S1+H.

Пошук максимального елемента списку.

Тут знадобиться допоміжний предикат max, що вибирає максимальне значення із двох елементів:

max(X,Y,X):- X>=Y.

max(X,Y,Y):- X<Y.

Результуючий предикат maxlіst(LІST,MAX), де MAX - найбільший елемент списку LІST, визначається так:

maxlіst([X],X).

maxlіst([X,Y|T],MAX):-

maxlіst([Y|T],MAXT), max(X,MAXT,MAX).

Зміст базового правила: максимальний елемент одноелементного списку дорівнює саме цьому елементу. Інакше, якщо в списку є хоча б два елементи X і Y, обирається максимальний елемент хвоста MAXT і при цьому MAX дорівнює найбільшому з X і MAXT.

Самостійні завдання

1. Дати альтернативні визначення наведених відношень й їхнього застосування.

2. Наведіть приклади задач, що використають розглянуті відношення.

3. Напишіть процедури мовою Пролог для рішення наступних задач і наведіть приклади їхнього використання:

   1. перестановки, сортування елементів списку чисел;

   2. визначення мінімального елемента, середньоарифметичного, добутку списку чисел;

   3. пошуку другого за величиною елемента списку;

   4. формування нового списку з тих елементів даного списку, які займають непарні позиції. Наприклад, зі списку чисел [1, 2, 3, 4, 5, 6, 7] потрібно одержати наступний: [1, 3, 5, 7].

4. Створіть предикат, що замінює у вихідному списку перше входження заданого значення іншим.

5. Створіть предикат, що замінює у вихідному списку всі входження заданого значення іншим.

6. Створіть предикат, що породжує по заданому натуральному числу N список, що складається з натуральних чисел від 1 до N (по зростанню).

7. Створіть предикат, що породжує по заданому натуральному числу N список, що складається з натуральних чисел від N до 1 (по убуванню).

8. Створіть предикат, що породжує по заданому натуральному числу N список, що складається з N випадкових натуральних чисел із проміжку від 1 до 100.

9. Створіть предикат, що породжує по заданих числах N, M, K список, що складається з N випадкових натуральних чисел із проміжку від M до K.

10. Створіть предикат, що породжує по заданих числах M, K список, що складається з випадкової кількості випадкових чисел із проміжку від M до K.

11. Створіть предикат, що породжує список, який складається з випадкової кількості випадкових чисел.

12. Створіть предикат, що збільшує елементи вихідного списку на одиницю.

13. Створіть предикат, що переводить список цифр від 0 до 9 у список відповідних їм назв (рядків).

14. Створіть предикат, що переводить список чисел у список відповідних їм назв.

15. Створіть предикат, що переводить список цифр від 0 до 9 у список відповідних їм римських чисел.

16. Створіть предикат, що переводить список арабських чисел у список відповідних їм римських чисел.

17. Створіть предикат, що переводить список римських чисел у список відповідних їм арабських чисел.

18. Створіть предикат, що подвоює значення елементів списку.

19. Створіть предикат, що перетворює список, елементами якого є числа, у список, елементи якого не від'ємні.

20. Створіть предикат, що перетворює вихідний список у список позицій негативних елементів.

21. Створіть предикат, що видаляє з вихідного списку елементи з парними номерами.

22. Створіть предикат, що розділить вихідний список із цілих чисел на два списки: список позитивних чисел і список негативних чисел.

23. Створіть предикат, що розділяє вихідний список на два підсписка. У перший з них повинні потрапити елементи з непарними номерами, у другий - елементи з парними номерами.

24. Створіть предикат, що обчислює за списком і числом, підсписок вихідного списку, що починається з елемента із зазначеним номером.

25. Створіть предикат, що здійснює видалення зазначеної кількості останніх елементів вихідного списку.

26. Створіть предикат, що здійснює поділ вихідного списку на два подсписка. У перший з них повинна потрапити зазначена кількість елементів з початку списку, у другий - елементи, що залишились.

27. Створіть предикат, що здійснює поділ вихідного списку на два подсписка. У перший з них повинна потрапити зазначена кількість елементів з кінця списку, у другий - елементи, що залишилися.

28. Створіть предикат, що знаходить передостанній елемент списку.

29. Створіть предикат, що видаляє передостанній елемент списку.

30. Створіть предикат, що замінює у вихідному списку два однакових елементи, що йдуть підряд, одним.

31. Створіть предикат, що видаляє у вихідному списку всі повторні входження елементів.

32. Створіть предикат, що здійснює перестановку двох елементів списку із заданими номерами.

33. Створіть предикат, що генерує всі перестановки елементів списку, заданого першим аргументом.

34. Створіть предикат, що здійснює циклічне зрушення елементів списку на один уліво (вправо).

35. Створіть предикат, що здійснює циклічне зрушення елементів списку на задану кількість кроків уліво (вправо).

36. Створіть предикат, що здійснює поелементне перемножування відповідних елементів двох вихідних списків.

37. Створіть предикат, що обчислює скалярний добуток векторів, заданих списками цілих чисел.

38. Створіть предикат, що здійснює підрахунок числа входжень кожного елемента вихідного списку. Відповіддю повинен бути список пар, у яких перший компонент - елемент вихідного списку, другий - число його входжень у первісний список.

39. Створіть предикат, що визначає першу позицію підсписка в списку.

40. Створіть предикат, що додає елементи одного списку в другий список, починаючи із заданої позиції.

41. Створіть предикат, що за списком і двом числам M і N повертає підсписок вихідного списку, що складається з елементів з номерами від M до N.

42. Створіть предикат, що формує список простих чисел, що не перевершують дане число.

43. Створіть предикат, що транспонує матрицю, задану списком списків.

44. Сформировать список [2, 4, 6, 8, 10] и удалить из него введенное число.

45. Сформировать списки [1, 3, 5, 7, 9] и [2, 4, б, 8, 10] и объединить их в один.

46. Сформировать список [3, 6, 9, 12, 15, 18] и вставить в него введенное число.

47. Сформировать список из N натуральных чисел, начиная с 10. Каждое следующее на 5 больше предыдущего.

48. Сформировать список [3, 6, 9, 12, 15] и найти сумму его элементов

49. Сформировать список [6, 5, 4, 3, 2] и найти сумму его элементов

50. Сформировать список [7, 5, 3, 1] и найти произведение его элементов

51. Сформировать список из N последовательных натуральных чисел, начиная с 10. Найти сумму его элементов