
Rete-алгоритм
Марковскі алгоритми є цілком певна стратегія керування – згідно порядку розташування правил, яка не є досить ефективним способом реалізації систем з багатьма правилами. Якщо потрібно створити експертну систему для реальних задач із сотень чи тисяч правил, то проблема ефективності стає найважливішою.
Фактично потрібен алгоритм, що має повну інформацію про всі правила й може застосувати будь-яке з них, не вживаючи повний перебір.
Рішенням проблеми є rete-алгоритм, відкритий Ч. Форгі в університеті Карнегі-Меллона в 1979 році при розробці експертної системи ОРS.
Rete-алгоритм заснований на використанні динамічної структури даних, подібної до В+ дерева, що автоматично реорганізується з метою оптимізації пошуку.
Висока швидкодія досягається для систем із прямим логічним виводом, завдяки зберіганню в оперативній пам'яті інформації про правила, що перебувають у мережі, та за рахунок обмеження обсягу роботи, необхідної для повторного обчислення конфліктної множини після запуску одного із правил.
Недолік алгоритму - великі потреби в пам'яті.
В основу rete-алгоритма покладена структура даних, запропонована на підставі двох емпіричних спостережень:
Часова надмірність. Кожне з правил, звичайно змінює лише кілька фактів, а кожна з цих змін впливає тільки на кілька правил.
Структурна подоба. Однаковий шаблон часто виявляється в лівій частині більше чим одного правила.
У наші дні rete-алгоритм продовжує залишатись важливим засобом підвищення швидкодії в тих випадках, коли система містить багато правил.
У rete-алгоритмі в кожному циклі контролюються тільки зміни в узгодженнях, тому в кожному циклі "розпізнавання-дія" не доводиться погоджувати факти з кожним правилом. Завдяки цьому істотно підвищується швидкість узгодження фактів з антецедентами, оскільки статичні дані, які не змінюються від циклу до циклу, можуть бути зігноровані.
Нижче наведено загальні відомості про технології, які утворюють фундамент сучасних експертних систем, заснованих на правилах.
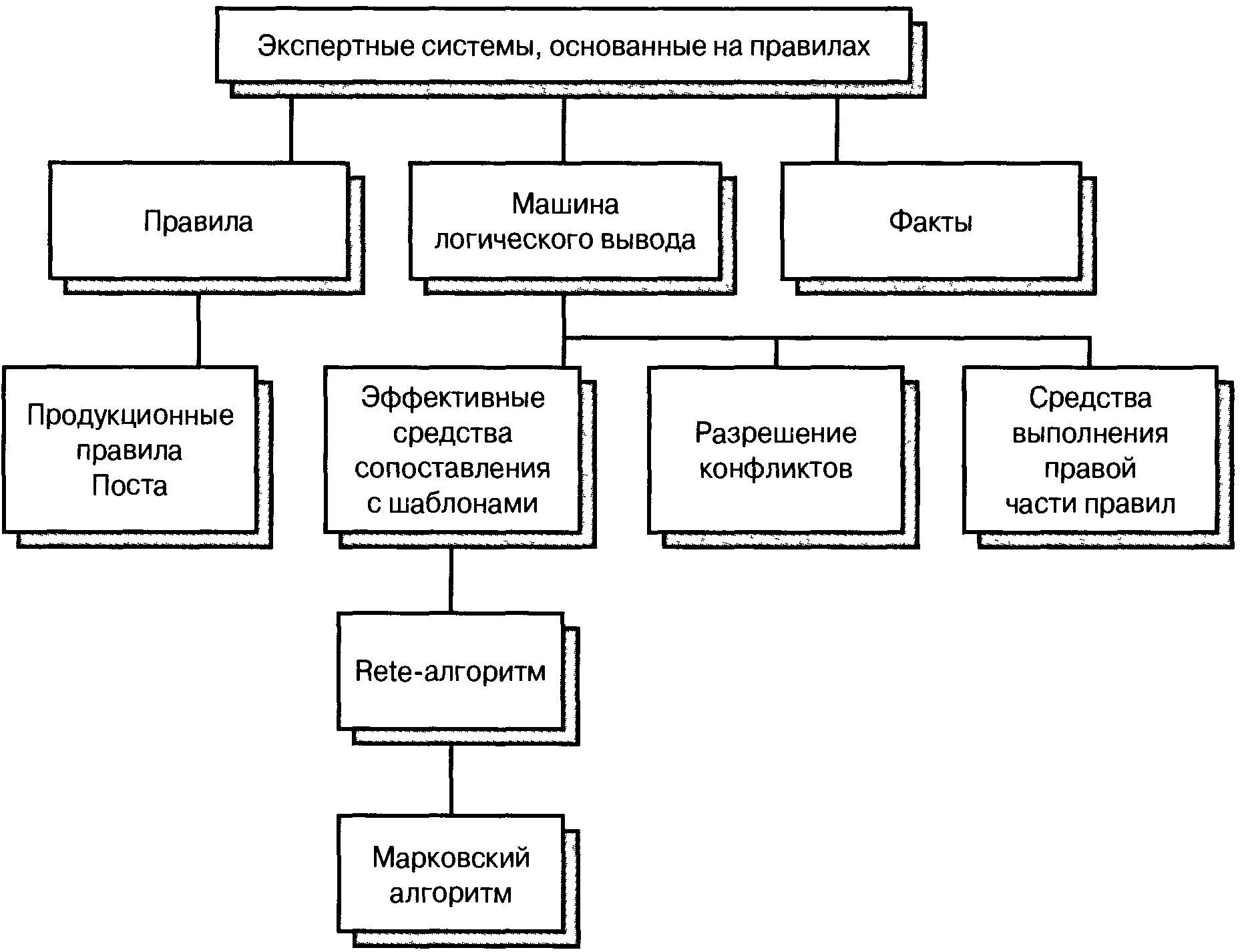
Основні недоліки систем продукцій:
труднощі складання продукційного правила, адекватного елементу знання, тому що важко виразити складні правила;
неможливий виклик одного правила з іншого (зв'язок між правилами тільки через дані);
відсутність внутрішньої структури веде до нерозв'язності проблеми несуперечності бази знань;
нема залежності кроків виводу від стратегії вибору, що ускладнює їхню інтерпретацію.
Висновок: "Продукційним системам не вистачає строгої теорії. Поки в них панує евристика. При заданій моделі проблемної області у вигляді сукупності продукцій не можна бути впевненим у її повноті й несуперечності. Причина невдач створення теорії криється в розпливчастості поняття продукції, у тій інтерпретації, що приписується ядру, а також у різних способах керування системою продукцій" [72, с. 55]
Семантичні мережі
Семантичні мережі, або просто мережі, - це класичний спосіб подання пропозиційної інформації у штучним інтелекті. Пропозиційним твердженням (або висловленням) є речення, що може бути істинним або ложним, таким як "усі собаки - ссавці" й "трикутник має три сторони". Висловлення мають форму декларативних знань, оскільки в них стверджуються факти.
З погляду математики семантична мережа є позначений орієнтований граф.
Семантичні мережі вперше були розроблені в 1968 році Квілліаном для досліджень в області штучного інтелекту як спосіб опису людської пам'яті й мови. Відтоді семантичні мережі успішно застосовувались для рішення багатьох задач подання знань. Розуміння змісту за допомогою семантичних мереж дозволяє вийти за межі можливостей програмного забезпечення простих ЕС або ШІ.
Структура семантичної мережі відображається графічно за допомогою вузлів і з'єднуючих їхніх дуг. Вузли іноді йменуються об'єктами а дуги - зв'язками, або ребрами.
Зв'язки в семантичній мережі застосовуються для подання відношень, а вузли, як правило, служать для подання фізичних об'єктів, концептів або ситуацій. Нижче показана звичайна мережа (фактично орієнтований граф), у якій зв'язки позначають авіаційні маршрути між містами. Вузли позначені кружками, а зв'язки - лініями, що з'єднують вузли. Стрілки показують напрямок, або орієнтацію, літаків, що роблять польоти (саме тому граф, на якому зазначені напрямки, називається орієнтованим).
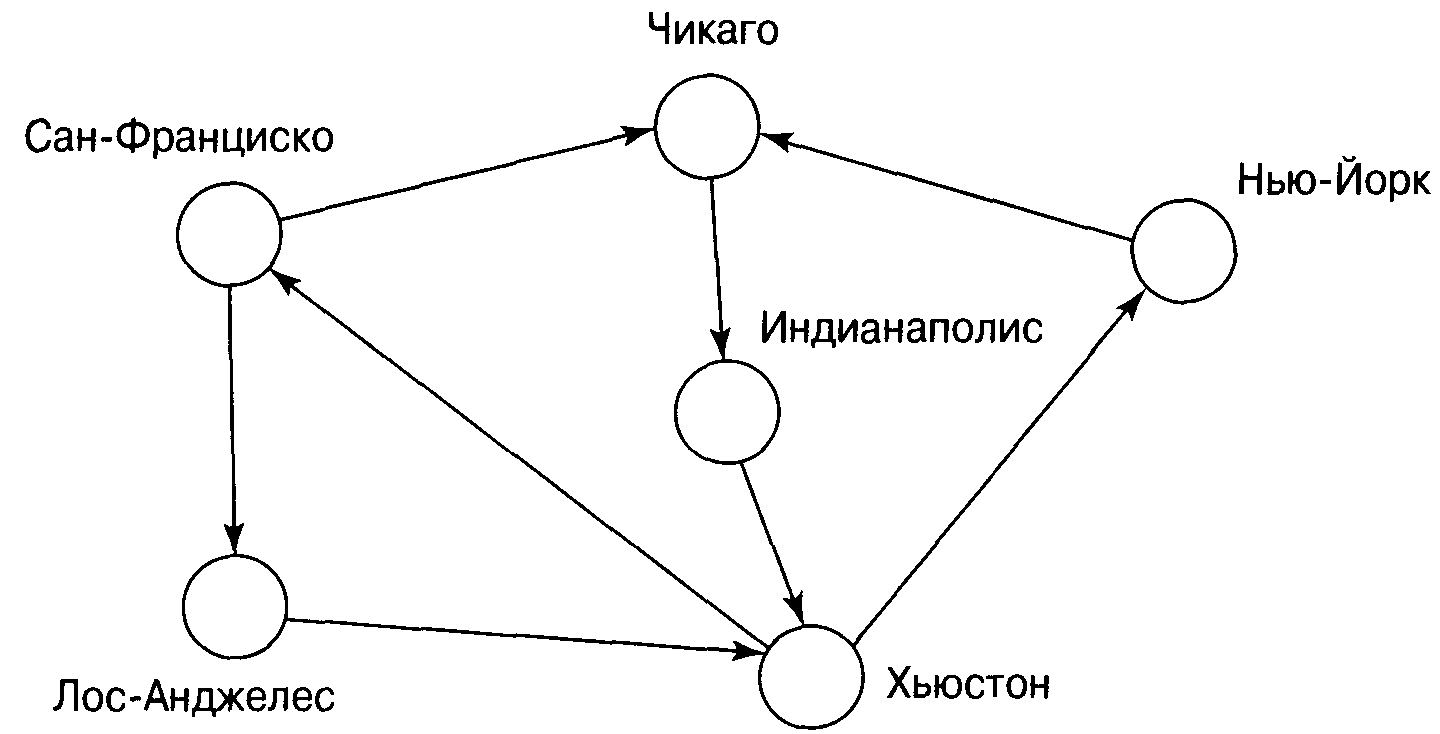
Мережа загального виду
На іншому малюнку зв'язками є відношення між членами деякої родини.
Для семантичних мереж відношення мають винятково важливе значення, оскільки надають знанням базову структуру. Без них знання стають лише колекцію незв'язаних даних. А при їхній наявності базові структури дозволяють виводити інші знання. Так, на підставі заданої структури можна зробити висновок, що Ганна й Білл - бабуся й дідусь Джона, незважаючи на те, що це відношення явно не задано.
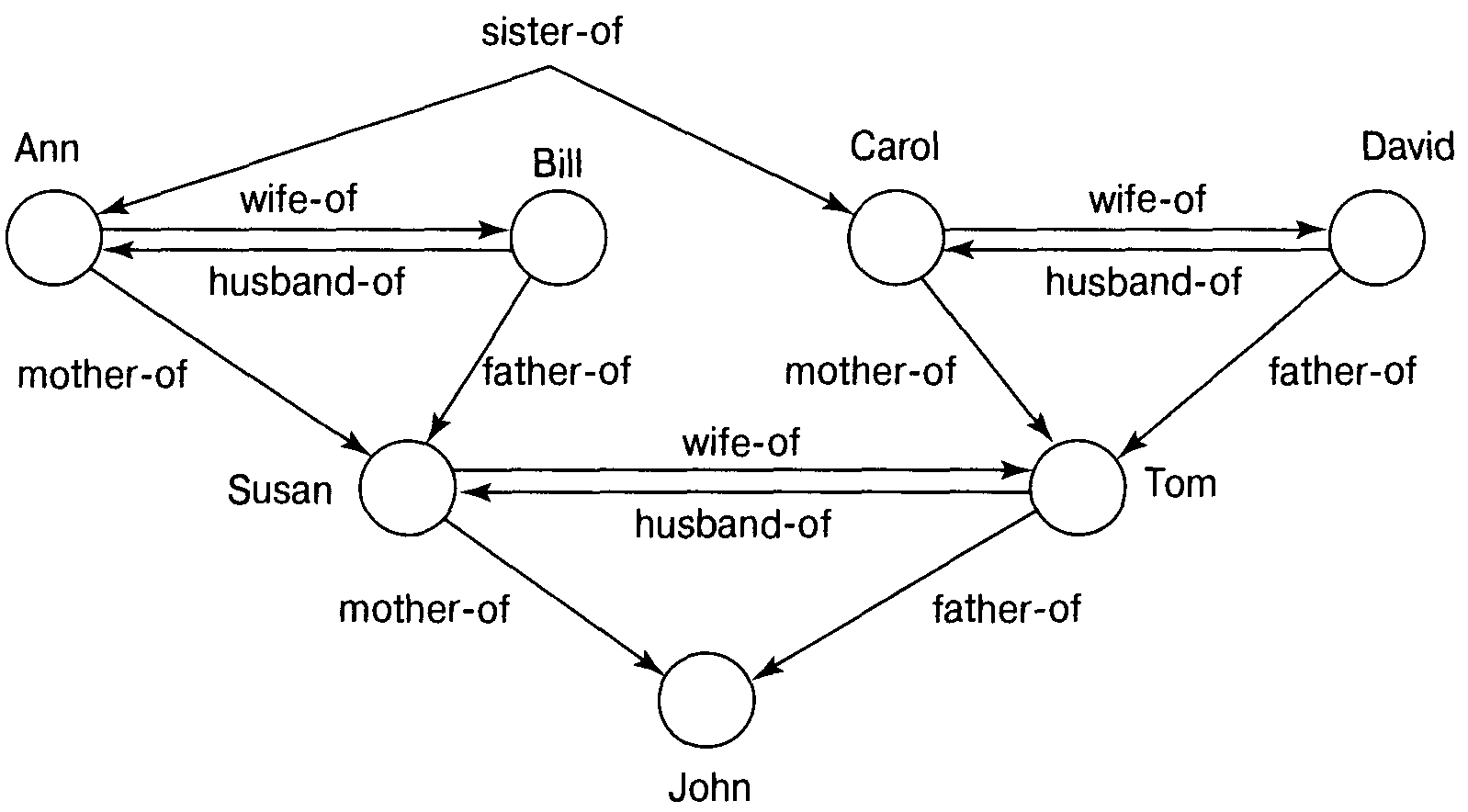
Семантична мережа
Семантичні мережі ще називають асоціативними мережами, оскільки одні вузли в таких мережах асоційовані або зв'язані з іншими. В оригінальній роботі Квілліана людська пам'ять моделювалась асоціативною мережею, де поняття були вузлами, а зв'язки показували їхнє з'єднання між собою. Згідно до цього, якщо при читанні слів речення стимулюється один вузол, то активізуються його зв'язки з іншими, і така активність поширюється по мережі. Якщо ж достатню активізацію одержує інший вузол, то у свідомості спливає концепція, представлена ним.
Наприклад, хоча людина знає тисячі слів, але в його свідомості відбиваються лише слова тої пропозиції, що він читає.
До двох найпоширеніших зв'язок належать is-a (є екземпляром) та a-kind-of (останню записують як АКО – є підмножиною, підкласом). При цьому більш загальний клас, на який указує стрілка АКО, називається суперкласом. Якщо суперклас має зв'язок АКО, що вказує на інший вузол, то він одночасно є класом суперкласу, на який вказує стрілка АКО.
Всі об'єкти класу повинні мати деякі спільні атрибути, кожен з них набуває значення. Комбінація атрибута й значення називається властивістю. Так, дирижабль має такі атрибути, як розміри, вага, форма й колір. Значенням атрибута форми є еліпсоїд. Іншими словами, властивістю дирижабля є еліпсоїдальна форма.
У семантичних мережах можна також знайти зв'язки інших типів.
Повторення характеристик вузла в його нащадках називається спадкуванням. Якщо не стверджується зворотне, то вважається, що всі елементи деякого класу успадковують всі властивості своїх суперкласів. Спадкування є корисний засіб у поданні знань, оскільки дозволяє загальні характеристики не вказувати повторно.
Зв'язки й спадкування є основою ефективних способів подання знань, даючи можливість показувати складні відношення за допомогою декількох вузлів і зв'язок.
