8.5. Аналитический способ определения частноортодромических координат места самолета по брлс
Точность определения КУО и дальности по бортовой РЛС и так не высока, а при графической работе на карте добавляются дополнительные погрешности. Кроме того, заниматься в полете графическими построениями, тем более пилоту, не очень удобно.
Учитывая, что для выдерживания ЛЗП нет необходимости получить МС именно как точку на карте, а достаточно знать ЛБУ и пройденное или оставшееся расстояние, можно предложить аналитический способ определения этих величин, то есть расчет их по формулам, без использования карты. По своему принципу этот способ аналогичен рассмотренному выше аналитическому способу определения координат по УДРНС. Он заключается в следующем.
Заранее, еще до полета, на карте измеряется координата zрло радиолокационного ориентира, то есть, насколько сбоку он находится от ЛЗП, а также измеряется расстояние sрло от траверза РЛО до расположенного впереди ППМ (рис. 8.11). Эти величины можно надписать на карте, поскольку они от полета к полету не меняются.
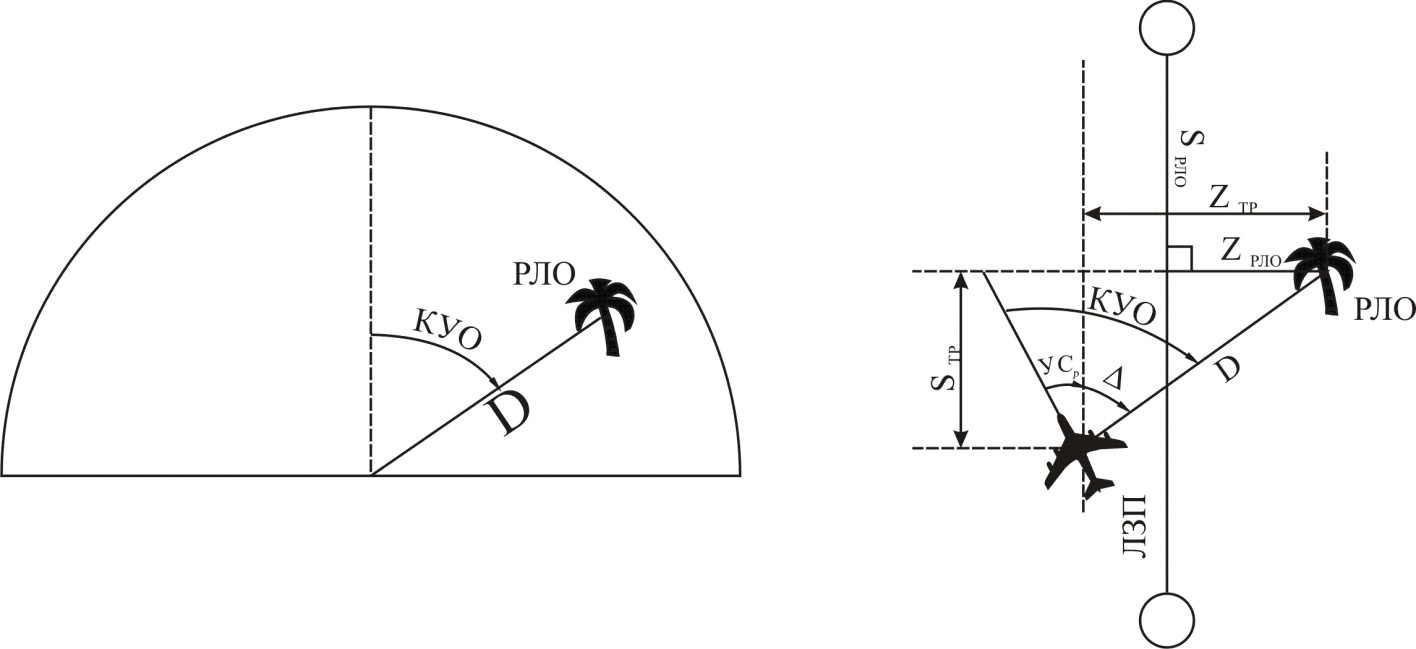
Рис. 8.11. Аналитический способ определения координат
В полете при появлении РЛО на экране измеряется КУО и дальность D до ориентира. Рассчитывается вспомогательный угол ∆ по формуле
∆ = КУО- УСр.
Здесь под УСр понимается просто разность заданного путевого угла и курса
УСр =ЗМПУ – МК.
Если самолет летит с расчетным курсом следования, то эта величина действительно будет расчетным углом сноса. Но если самолет летит с каким-то другим курсом (например, выходит на ЛЗП), то это просто величина, показывающая, на сколько курс отличается от ЗМПУ.
Далее рассчитываются
zтр = D sin ∆,
sтр = D cos ∆.
Величина zтр это боковое удаление ВС от РЛО (по направлению, перпендикулярному к ЛЗП). Если бы ВС находилось на ЛЗП, то эта величина совпала бы с zрло. Сравнив zтр с zрло легко определить, на какую величину самолет уклонился от ЛЗП.
А sтр это просто расстояние от самолета до траверза РЛО вдоль ЛЗП. Поскольку расстояние от траверза до ППМ известно, то нетрудно определить оставшееся расстояние до ППМ:
sост = sтр + sрло.
Приведенные формулы работают при любом расположении ориентира и при любом угле сноса, если не забывать про знаки входящих в них величин.
Рис. 8.11 соответствует случаю, когда РЛО находится справа от ЛЗП. Приведем пример расчета для случая, когда РЛО расположен слева от ЛЗП. Рисунок, соответствующий этому примеру читателю предлагается представить самостоятельно.
Пусть zрло= -30 км (минус означает, что РЛО слева);
sрло = 100 км (это расстояние от траверза до лежащего впереди ППМ).
Пусть ЗМПУ=220 , МК= 223, КУО= 348, D=130 км.
Находим УСр= ЗМПУ-МК=220-223=-3. Как уже отмечалось, это вовсе не значит, что УС составляет -3°. Это просто значит, что продольная ось отклонена вправо на 3° от направления ЛЗП.
Находим ∆=КУО-УС. Для удобства расчета на НЛ-10 можно вместо КУО=348 взять КУО= -12 (это тот же самый угол).
∆= 348- (-3)=351,
или, что то же самое,
∆=-12-(-3)= -12+3= -9.
Далее:
zтр = 130 sin (-9)= -20,
sтр = 130 cos (-9) = 128.
Косинус функция четная, поэтому sтр получилось положительным. Впрочем, в таких задачах эта величина всегда будет положительной. Ведь это расстояние, оставшееся до траверза, который всегда находится впереди (заднюю полусферу БРЛС не наблюдает).
Следовательно, до траверза РЛО осталось лететь 128 км и еще от траверза до ППМ 100 км. Значит, оставшееся расстояние 228 км.
Если бы самолет находился на ЛЗП, то боковое расстояние до него было бы 30 км (это zрло), а по расчету получилось 20 км (это zтр). Знак минус просто говорит о том, что РЛО слева. Следовательно, самолет ближе к РЛО, чем надо, на 10 км, то есть ЛБУ= -10 км.