1.3. Порядок работы навигатора при полете по марщруту
Порядок работы экипажа в полете по маршруту. Полет по маршруту начинается после выполнения схемы вылета еще до того, как ВС набрало заданную высоту. Но с точки зрения выдерживания ЛЗП не имеет большого значения, летит ВС в наборе или горизонтально.
После занятия заданного эшелона необходимо:
- уточнить МС;
- записать в штурманский бортовой журнал высоту, температуру воздуха и остаток топлива;
- рассчитать истинную воздушную скорость (она пересчитывается также при каждом изменении эшелона).
Маршрут состоит из нескольких участков – от ППМ до ППМ, которых может быть довольно много. Независимо от протяженности участка на каждом из них выполняются практически одни и те же операции. Поэтому работа навигатора на маршруте носит в значительной степени циклический характер.
На каждом участке маршрутного полета навигатор выполняет следующие операции:
- при пролете ППМ включает секундомер и докладывает диспетчеру о пролете пункта (свой позывной, наименование пункта, высоту, расчетное время следующего ППМ);
- по окончании разворота на очередной участок маршрута проверяет правильность взятого курса путем проверки его соответствия заданному путевому углу (с учетом расчетного угла сноса) и сопоставления с показаниями дублирующих курсовых приборов;
- записывает в штурманском бортовом журнале время пролета ППМ, курс и высоту, расчетное время следующего ППМ;
- уточняет расчетное время пролета последующих ППМ и время прибытия на аэродром назначения;
- настраивает радиотехнические средства навигации и устанавливает на пультах навигационных систем данные, необходимые для полета на данном участке маршрута;
- периодически осуществляет контроль и исправление пути;
- рассчитывает курс следования и путевую скорость на следующем участке маршрута по фактическому ветру;
- примерно за 2 минуты до пролета ППМ прекращает выполнение других операций и осуществляет контроль пролета ППМ.
Но есть операции, которые нужно выполнять не на каждом участке. Периодически, по мере необходимости, навигатор:
- определяет путевую скорость и угол сноса;
- определяет направление и скорость ветра;
- выполняет контроль и коррекцию ухода гироскопических курсовых приборов;
- устанавливает широту пролетаемой местности;
- контролирует остаток топлива и уточняет рубеж ухода на запасной аэродром;
- прослушивает эфир и, по поручению командира ВС, ведет радиосвязь.
Разумеется, на некоторых современных типах ВС значительная часть перечисленных операций автоматизирована. Но и в этом случае за экипажем сохраняется обязанность непрерывного контроля за работой бортовых навигационных систем и готовность вмешаться в навигационный процесс при любых непредвиденных отклонениях от плана полета.
1.4. Определение путевой скорости и угла сноса на контрольном этапе
Это один из самых простых и древних способов определения таких важных навигационных элементов полета как путевая скорость и угол сноса. Эти величины необходимо знать пилоту не только для того, чтобы правильно определить курс следования и оставшееся время полета до очередного ППМ, но и для того, чтобы определить фактический ветер. Ведь это даст возможность рассчитать путевую скорость, время, угол сноса и курс и для последующих участков маршрута.
Для определения W и УС данным способом необходимо определить место самолета в два разных момента времени, при этом между ними выдерживать постоянный курс. Собственно, отрезок пути между этими двумя МС и называют контрольным этапом.
Каким способом получено каждое из этих двух МС, визуально или с помощью радиотехнических средств, – не имеет значения. Разумеется, чем точнее они определены – тем лучше.
В момент, когда определено первое МС включается секундомер, фиксируется курс и выдерживается постоянным. Через 10-20 мин снова определяется МС и фиксируется время на секундомере. Оба МС наносятся на полетную карту.
Нетрудно сообразить, как определить путевую скорость. Для этого нужно знать время полета на контрольном этапе (оно определено по секундомеру) и пройденное за это время расстояние – а его можно просто измерить на карте от одного МС до другого.
Для определения УС два полученные МС нужно соединить на карте прямой линией. Эта линия и будет линией фактического пути. Ведь выдерживался постоянный курс, следовательно, на контрольном этапе самолет летел «по прямой».
Угол сноса – это угол между векторами истинной воздушной скорости и путевой скорости. Вектор V направлен по продольной оси ВС, следовательно его направление, это курс. Вектор W направлен по ЛФП, его направление – это фактический путевой угол. Но ЛФП уже изображена на нашей карте, поэтому это направление можно просто измерить транспортиром. На карте направления можно измерить только от истинных меридианов, поэтому будет измерен ФИПУ.
Строго говоря, поскольку меридианы не параллельны, значение ФИПУ будет несколько различным, в зависимости от того в какой точке ЛФП мы его измерим. Разумно измерить его от среднего меридиана ЛФП, ведь речь идет об определении среднего УС на данном участке.
Полученный ФИПУ нужно сравнить с курсом, но, конечно, тоже истинным. Чтобы преобразовать выдерживаемый на контрольном этапе МК в ИК нужно в соответствии с правилом учета поправок прибавить магнитное склонение. Поскольку оно тоже может быть различным в разных местах карты, целесообразно использовать среднее его значение на данном участке полета.
ИК=МК+ΔМ;
УС=ФИПУ-ИК.
Например, если ИК=115, и измерен ФИПУ=112, то УС=-3. Ведь самолет сносит влево: продольная ось ВС направлена в направлении 115º, а летит самолет в направлении 112º.
Точность определения W и особенно УС таким способом не слишком высока. Она зависит от того, насколько точно определено каждое МС, от случайных погрешностей графической работы на карте (измерения расстояний и направлений). Но также важно помнить, что точность зависит от длины контрольного этапа, которую выбирает сам пилот. Она не должна быть слишком малой, иначе точность определения навигационных элементов может оказаться слишком низкой.
Это связано с тем, что как измеренная длина контрольного этапа, так и время полета на нем определяются с погрешностями. Погрешностью измерения времени можно пренебречь, поскольку с помощью секундомера время измеряется достаточно точно. А вот погрешность определения длины контрольного этапа зависит в первую очередь от точности определения мест самолета, то есть от того, каким способом они определены. Кроме того, дополнительная погрешность возникает при измерении этой длины на карте. Ведь расстояние измеряется пилотом линейкой и вряд ли может быть измерено с погрешностью меньше, чем полмиллиметра. А в зависимости от масштаба карты миллиметр может соответствовать расстоянию и в 1, и 2, и в 4 км.
Допустим, длина контрольного этапа S определена пилотом с погрешностью ΔS.
Тогда фактическая путевая скорость
а рассчитанная по результатам измерения на карте скорость
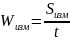
Тогда погрешность измерения скорости ΔW=Wизм – W составит
Поделим левую и правую части этого равенства на W и учтем, что в знаменателе правой части Wt=S. Получим
Таким образом, относительная погрешность определения путевой скорости, то есть отношение ΔW к самой W, равна относительной погрешности определения длины контрольного этапа. Очевидно, что тогда абсолютная погрешность путевой скорости
Рассмотрим несколько примеров, основанных на этой формуле. Пусть самолет пролетел контрольный этап длиной S=100 км за t=10 мин. Очевидно, что тогда W=600 км/ч.
Предположим, что длина контрольного этапа определена с погрешностью ΔS=2км. Тогда
Это неплохая точность определения скорости, если учесть что на указателе воздушной скорости цена деления 10 км/ч. Да и ДИСС измеряет путевую скорость не на много точнее.
Но если бы длина контрольного этапа была в два раза меньше (S=50 км) при той же точности измерения его длины, то погрешность определения путевой скорости, как следует из формулы, была бы вдвое больше:
Такая точность уже не столь хороша, хотя для практики вполне приемлемая.
А теперь представим себе, что пилот решил измерить путевую скорость на контрольном этапе длиной всего 10 км. Действительно, затем лететь и ждать результата 5-10 мин? Ведь хочется побыстрее. Но тогда
То есть, фактическая путевая скорость 600 км/ч измерена пилотом с погрешностью 120 км/ч. Это значит, что он получил бы значение 720 или 480 км/ч, в зависимости от того, в большую или меньшую сторону он ошибся. И кому нужна путевая скорость, полученная с такой точностью?
В данном примере мы задались конкретным значением погрешности ΔS=2 км. Но ведь на самом деле величина этой погрешности случайная и пилот никогда не знает, на сколько именно он ошибся. Соответственно случайной будет и ΔW. Она останется неизвестной и пилот не может с ее помощью исправить измеренное значение путевой скорости.
Приведенные рассуждения касались определения путевой скорости. Но их можно было бы повторить и применительно к определению угла сноса. Здесь основную роль играла бы не продольная погрешность определения длины контрольного этапа ΔS, а линейные погрешности определения каждого МС в поперечном (по отношению к ЛФП) направлении. Ведь боковое смещение МС привело бы к ошибке в измеренном ФИПУ.
Из формулы ( ) следует, что чем больше длина контрольного этапа S, тем точнее определяется путевая скорость. Казалось бы, что следует стремиться к увеличению этой длины. И, например, при S=1000 км получили бы замечательную точность (для условий нашего примера погрешность была бы около 1 км/ч).
Но не следует, пользуясь мощью математики, забывать о реальности, которую эта математика должна описывать.
Во-первых, в гражданской авиации полеты выполняются по установленным маршрутам, на которых длина участка редко превышает 300 км. Как же в этом случае пролететь тысячу километров с постоянным курсом?
Во-вторых, ветер в пространстве меняется и, соответственно меняется путевая скорость. Понятно, что рассмотренным способом определяется средняя путевая скорость и средний угол сноса на данном участке. Конечно, в соответствии с формулой ( ) среднюю путевую скорость мы бы определили достаточно точно. Фактическая мгновенная W совпадала с этой средней W где-то посередине контрольного этапа. Но она ли нужна пилоту? Ему нужна та W, которая имеет место именно сейчас, в момент окончания ее измерения. Ведь по ней будет, рассчитываться, например, расчетное время пролета следующего ППМ. Зачем пилоту значение W, которое имело место где-то 500 км назад? Ведь оно может значительно отличаться от текущей путевой скорости.
Таким образом, в соответствии с формулой ( ) для повышения точности определения W следует выбирать дину контрольного этапа возможно больше. Но из-за изменчивости ветра полученное среднее значение W становится все более далеким от текущего ее значения (в конце этапа).
Математический анализ и авиационная практика показывают, что достаточная точность определения W и УС может быть достигнута при длине контрольного этапа порядка 100 км. В любом случае эта длина не должна быть менее 40-50 км, в противном случае точность может оказаться совсем неудовлетворительной.