Практическое занятие 9. Конверсия финансовых рент и анализ переменных денежных потоков

Цель:Изучить принцип расчета параметров конверсионных рент для использования в практических расчетах.

Расчет единовременного платежа при выкупе ренты производится по формуле

R=A*PVIFA_n,i*n*V^t ,

где A – размер единовременного платежа;

R – элемент ренты;

PVIFA_n;i – множитель приведения;

n – срок реализации ренты;

i – процентная ставка, используемая по согласованию сторон для расчета конверсионных параметров;

V – множитель наращения V = (1+i);

t – временной период, соответствующий периоду отсрочки выплаты единовременного платежа.

При заданном сроке ренты определить размер регулярного платежа позволяет формула

A=PV/PVIFA_i,n,

При заданном размере платежа определить срок ренты возможно по следующей формуле

PVIFA_i,n = PV/A,

Современная величина консолидированной ренты определяется с использованием формулы

где PV – современная ценность консолидированных рент;

PVq – современная ценность q-ренты из совокупности объединенных рент;

k – количество объединенных рент.

Размер элемента консолидированной ренты при заданном сроке реализации консолидированной ренты определяется по формуле

где A_q – элемент q-й объединяемой ренты;

PVIFA_nq,iq – множитель приведения q-ренты;

i_q – % ставка, используемая для приведения q-й ренты;

n – срок реализации консолидированной ренты;

i – % ставка, используемая для конверсионного преобразования.

Элемент ренты в случае отсрочки, если сроки ренты остаются неизменными (n₀=n₁) рассчитывается по формуле

A₀* PVIFA_{n,i =} A₁* PVIFA_n,i*^t ;

A₁=A₀V^t=A₀ (1+i)^t ;

где A₀ – платеж первоначальной ренты;

A₁ – платеж отсроченной ренты;

t - период отсрочки ренты;

V - элемент дисконтного множителя (1+i) ^-1

Элемент ренты в случае отсрочки, если сроки ренты изменяются (n₀≠n₁) рассчитывается по формуле

A₁=A_{0 *} (PVIFA_n0,i / PVIFA_n1,i )* V^t ,

где n₀ – срок первоначальной ренты;

n₁ – срок отсроченной ренты.

Период отсроченной ренты, если размеры платежей ренты остаются неизменными (A₀ = A₁) вычисляется по формуле

В случае замены годовой ренты с параметрами R_{0 ,} n₀ на р-срочную ренту с параметрами R_1, n_1, р, расчет элемента новой ренты производят по формуле

A₁=A_{0 *} PVIFA_n,i / PVIFA_n,i * k_PV,i ,

Современная и наращенная ценность финансовой ренты с постоянным абсолютным изменением элемента рассчитывается по формуле

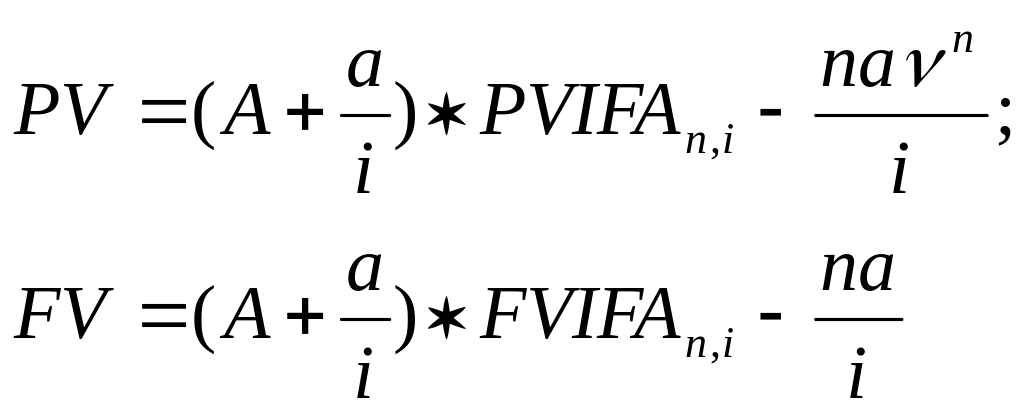
где РV – современная ценность переменной финансовой ренты;

FV – наращенная сумма переменной финансовой ренты;

R – начальное значение ряда, характеризующее поток;

a – ежегодный абсолютный прирост выплат или поступлений.

Задачи

1. Гражданин в течение 5 лет ежеквартально должен был выплачивать 500 грн.., погашая взятую ссуду. В связи с отъездом за границу через 2 года, он попросил перечислить величину ежеквартальной выплаты, чтобы успеть рассчитаться. Ставка процентов в банке – 8% годовых.

2. Заменить аннуитет по 10 тыс.грн. в год на эквивалентный аннуитет, выплачиваемый: а) поквартально; б) помесячно; в) через каждые полгода, если процентная ставка составляет 6% годовых.

3. По контракту приходится выплачивать 200 грн. в конце каждых 2-х месяцев в течение 3-х лет. Найти эквивалентную наличную сумму такого контракта, если деньги стоят J₁₂ = 36%.

4. Дом, оцененный за 120 тыс. грн. продаётся за 20 тыс. грн. наличными с последовательными одинаковыми годовыми платежами в течение последующих 10 лет. Какими должны быть платежи при норме процентов: а) J₁ = 4,5%; б) J₄ = 8%.

5. Три ренты постнумерандо – годовые, заменяются одной, отложенной на три года рентой постнумерандо. Согласно договорённости заменяющая рента имеет срок 10 лет, включая отсрочку. Характеристики заменяемых рент: платежи соответственно 100 грн., 120 грн., 300 грн.; сроки этих рент 6,11, 8 лет. Ставка сложных процентов годовых 20%. Определить размер платежа заменяющей ренты.

6. Требуется объединить три финансовые ренты в одну с квартальными платежами и квартальным начислением процентов. Срок объединённой ренты – 2 года. Номинальная процентная ставка – 30%. Платежи объединённой ренты откладываются на пол года. Условия объединения рент приведены в таблице 1, где т и р – число периодов начисления процентов и платежей в году; j – номинальные процентные ставки ренты; t – продолжительность периода, на который откладываются денежные платежи; R – разовые рентные платежи.

Таблица 1

№ ренты	Срок ренты, n лет	t	p	A, лет	R, тыс.грн	j, %
I	1	4	4	0	18	36
II	2	6	6	0	24	24
III	2,5	12	2	1	36	28