3.9.2. Реализация фильтров верхних частот, полосовых и заграждающих фильтров

М ожно напрямую рассчитывать различные типы фильтров. В инженерном плане выбран путь замены требований ФВЧ, полосовых и заграждающих фильтров на требования ФНЧ, который называется ФНЧ- прототипом. Это удобнее, поскольку все полиномы и расчетные формулы в справочниках приводятся для НЧ характеристик. При этом вводят расчетную частоту Ω_Р. Для получения характеристик других типов фильтров из характеристик ФНЧ прототипа применяют преобразование частоты – математическая операция замены частоты на другую по соответствующей формуле → p=1/p^′ для ФВЧ и p=p^′+1/p^′ для ПФ.

Рассмотрим характеристику ослабления ФНЧ. Сплошная линия – характеристика ФНЧ – прототипа, пунктирная – похожа на характеристику ФВЧ. Она получится при замене частоты на 1/p^′ (зеркальное отражение → 0 переходит в ∞, а ∞ в 0), В схеме ФВЧ индуктивность прототипа заменится емкостью, емкость – индуктивностью (pL переходит в L/p^′, а это сопротивление емкости 1/L). Это напоминает принцип дуальности. Фазовая характеристика ФВЧ будет соответствовать фазовой ФНЧ, но с обратным знаком.

Объединение двух кривых дает характеристику ПФ (повторение и отражение, а граничная частота соответствует средней частоте f₀).Полосовой фильтр получается c учетом преобразования частоты путем объединения ФНЧ и ФВЧ (р′+1/p′). В схеме ПФ индуктивность прототипа заменится последовательным контуром,

(pL=p′L+L/p′), а емкость параллельным (рС=р′С+С/p′). Для ФВЧ , - для ФНЧ прототипа. При Ω=∞ Ω_Р=0, что соответствует 0 ослабления ФНЧ прототипа. Для ПФ > 1 и <1. Вводят параметр коэффициента преобразования ПП при переходе от полосового фильтра к прототипу поскольку ПП в ПФ не всегда равна ПП ФНЧ- прототипа:

. Здесь f₂ – верхняя граничная ПП, а f^/′₂ – нижняя граничная. Расчетная частота полосового фильтра для ФНЧ- прототипа:

. При Ω=1 Ω_Р=0, что соответствует 0 ослабления ФНЧ прототипа.

Замена элементов ФНЧ – прототипа элементами ФВЧ и ПФ.

Нормированные элементы схемы ФНЧ-прототипа	Нормированные элементы схемы ФВЧ	Нормированные элементы схемы ПФ

Количество элементов в полосовом фильтре в два раза больше. Фазовая характеристика получается двойная: одна часть от ФНЧ (положительная), другая – от ФВЧ (отрицательная).

- резонансная частота колебательных контуров, входящих в схему фильтра.

Для реализации заграждающего фильтра берется преобразование частоты обратное преобразованию для полосового фильтра . Индуктивность прототипа при этом переходит в параллельный колебательный контур, а емкость – в последовательный.

3.9.3. Денормирование по сопротивлению и по частоте

при расчете величин элементов

По сопротивлению :

По частоте:

• для ФНЧ: , для ФВЧ: , где , Ω₂ и Ω_2р=1

• для ПФ: , где и Ω_2р=1

• для индуктивности

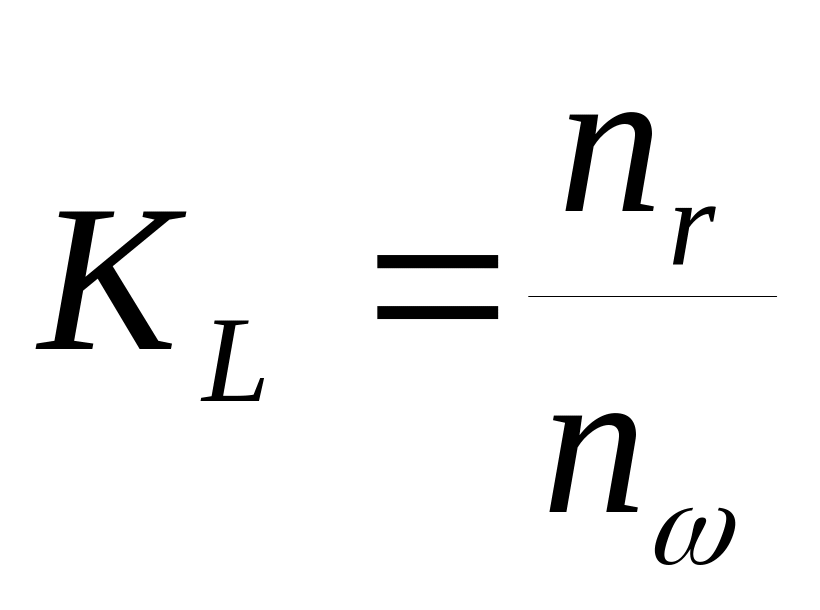
• для емкости .

Ускоренный метод синтеза схем фильтра по Попову

Попов П.А. установил, что схемы фильтров либо симметричные (n – нечетное) и состоят из 2 одинаковых половинок, либо асимметричные и состоят из двух обратных половинок (n – четное). Тогда можно синтезировать только одну половину фильтра, другую - достраивать.

Ускоренный метод реализации симметричных фильтров

(n-нечетное)

Представим нормированную схему фильтра в виде двух каскадно-соединенных одинаковых четырехполюсников, в которой выполняются следующие соотношения:

,

,

,

Представление фильтра в виде двух каскадно - соединённых согласованных четырехполюсников.

(при согласованном соединении таких четырехполюсников элементы и в матрице меняются местами), где , , , , — полиномы комплексной частоты с вещественными коэффициентами, — общий знаменатель у всех элементов — матрицы.

Рассматриваемый метод называется ускоренным потому, что достаточно сформировать функцию входного сопротивления по найденной на этапе аппроксимации функции и реализовать только (правую) половину фильтра. Левая часть достраивается, исходя из условия симметрии .

Из теории четырехполюсников известно:

,