Потери ветряных двигателей

Потери ветряных двигателей разделяются на четыре группы [35].

1. Концевые потери, происходящие за счёт образова­ния вихрей, сходящих с концов лопастей. Эти потери определяются на основании теории индуктивного сопро­тивления. Часть этих потерь была учтена при выводе идеального коэффициента использования энергии ветра _i ; неучтенная часть концевых потерь выражается формулой (126):

(126)

2. Профильные потери, которые вызываются трением струй воздуха о поверхность крыла и зависят только от профиля лопастей.

Мощность, поглощаемая профильным сопротивлением элементарных лопастей длиною dr, на радиусе r ветряка равна: (127)

где С_р— коэффициент профильного сопротивления, кото­рый для крыла бесконечного размаха равен С_х, т. е.: C_p = C_x. Так как или C_x =  C_у, то C_р =  C_у.

Подставляя значение С_р, равное  C_у и в уравнение (127), получим:

Подставляем значение ibC_y из уравнения (95) и делаем преобразования этого уравнения:

Подставляем: ; ; и отбрасываем в знаменателе μ, по сравнению с z_u:

как малую величину,

Интегрируя в пределах от 0 до Ζ получим:

Профильные потери там, где уже кончилась лопасть, существуют в виде сопротивления маха, каковое, таким образом, учитывается приблизительно. В результате ин­тегрирования получаем профильные потери всего вет­ряка: , где μ' = есть средняя величина по всей лопасти.

Так как и , то, подставляя значе­ния этих выражений в данное уравнение и разделив его на получим окончательную формулу профильных потерь в безразмерном значении: (128)

3. Потери на кручение струи за ветряком равны живой силе тангенциальных скоростей уходящей струи. Вели­чину этих потерь получим, проинтегрировав живую силу от тангенциальных скоростей всех элементарных струй в пределах от r₀ до R , а именно: (129)

Заменим в данном выражении u₂ его значением, которое равно 2u₁. Так как на основании уравнений (106) и (102) , и получим:

следовательно: откуда: или (130)

Подставляя значение u₂ в уравнение (129), получим:

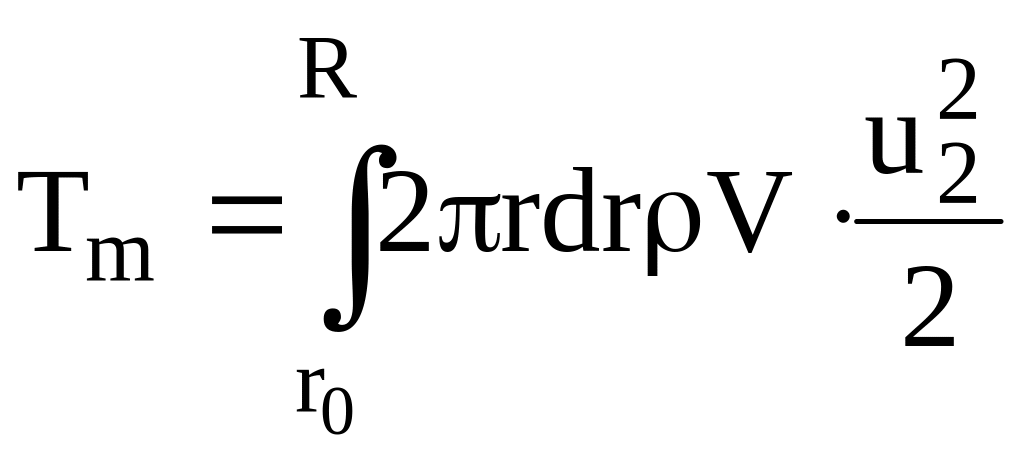
Вынося постоянные за знак интеграла и заменив η некоторым его значением ₁, средним для всего радиуса r, получим:

Поделив обе части этого равенства на мощность идеаль­ного ветряка:

получим отвлечённую величину потерь на кручение струи за ветряком: (131)

4. Потери, происходящие вследствие неполного исполь­зования всей ометаемой площади, учитываются отноше­нием: Полезную мощность, развиваемую ветряком, получим, вычтя все потери из мощности идеального ветряка:

Разделив правую и левую части этого уравнения на выражение энергии ветра , получим коэффициент использования энергии ветра реального ветряка: (133)

Так как, согласно уравнению (101),  = _i η, нахо­дим, что относительный коэффициент полезного действия η ветряка равен: (134)

Аэродинамический расчёт ветроколеса

Конструктивная схема 4–лопастного ветроколеса дана на рис. 58. Для расчёта должны быть заданы:

1) мощность N в лошадиных силах, которую необходимо получить от ветродвигателя;

2) скорость ветра V, при которой ветродвигатель дол­жен развивать эту мощность;

3) число модулей или быстроходность Ζ ветряка при максимальном коэффициенте использования энергии ветра данного типа ветряка;

4) коэффициент использования энергии ветра  .

Расчёт начинают с определения диаметра ветроколеса D, исходя из уравнения мощности ветродвигателя в лошадиных силах, которую получим, разделив уравнение (62) на 75 и умножив на коэффициент использования энергии вет­ра , т. е.: (135) где – массовая плотность воздуха принимается при температуре t = 15°С и давле­нии атмосферы Р₀ = 760 мм рт.ст.

Подставляя значение ρ = 0,125 в уравнение (135), получим мощность ветродвигателя, выраженную в за­висимости от ометаемой поверхности ветроколеса любой системы для условий t = 15°С и Р₀ = 760 мм рт.ст.

(136)

Так как для крыльчатого ветряка ометаемая поверхность S (рис. 58) равна:

то можем выразить мощность крыльчатого ветряка в зависимости от его диаметра D.

Ν = 0,000833·0,785 D²V³ = 0,000654 D² V³  л. с. (137) или

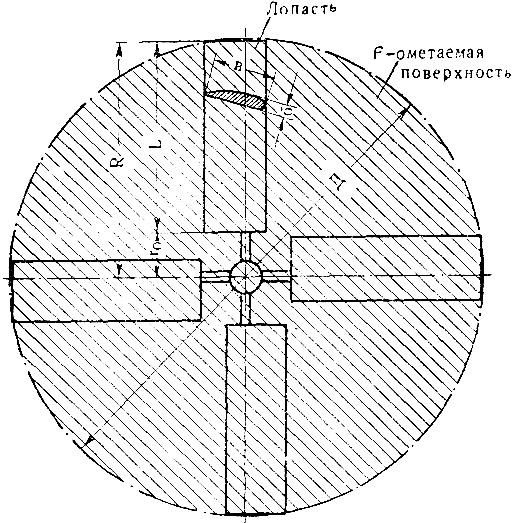
Рис. 58. Схема ветроколеса.

Мощность ветродвигателя в киловаттах напишется так: N = 0,000481 D² V³  квт. (138)

Диаметр ветроколеса заданной мощности в лошади­ных силах будет равен:

(139)

Для другой температуры t и давления P мощность надо определить при соответствующей массовой плотности ρ, которая определяется формулой. Внося эту поправку в уравнение мощности, получим:

и соответственно диаметр ветроколеса будет равен: (139а)

Скорость ветра V, при которой ветроколесо должно раз­вивать заданную для расчёта мощность, обычно прини­мают равной от 8 до 14 м/сек. (см. гл. IX). Число модулей Ζ либо задаётся, либо определяется, если заданы обороты n ветроколеса: отсюда: (140)

Далее, на основании конструктивных соображений и опытных данных продувок, выбирают толщину профиля лопасти. На конце лопасти берут профиль толщиной  = 0,1b до 0,15b, где b – ширина лопасти.

К втулке тол­щина профиля δ увеличивается, достигая у ветряков с поворотными лопастями около оси маха от 0,2b до 0,35b.

Для решения уравнений, определяющих форму ло­пастей, число их и коэффициент использования энергии ветра, задаются несколькими значениями коэффициента торможения е, например, е = 0,3; 0,35; 0,40, и опреде­ляют идеальный коэффициент использования энергии ве­тра . Затем с помощью уравнений (126), (128), (131) и (133) определяют  и строят кривую зави­симости  от е и выбирают e, соответствующее ξ_mах . После этого строят расчётную таблицу 6, где в верхней части таблицы приведены основные формулы расчёта.

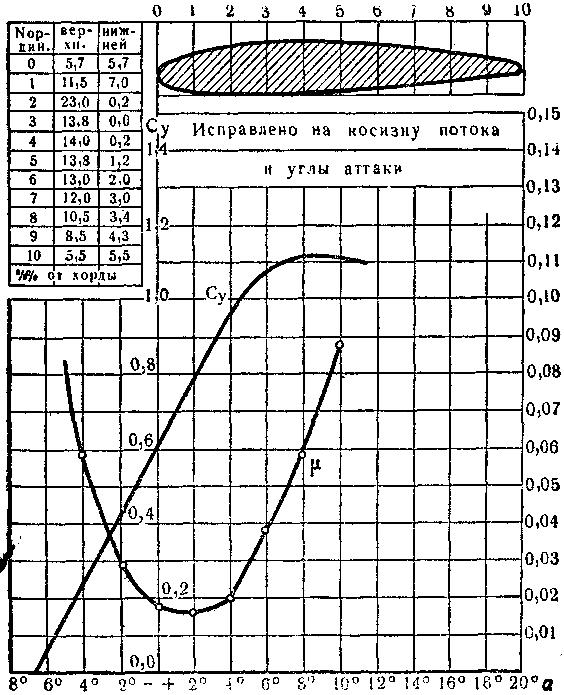
Рис. 59. Кривые для определения С_у и  в зависимости от .

В графе 1 приведены радиусы сечений лопасти в относительных величинах ; Каждая горизонтальная строка таблицы с цифрами соответствует данному сечению лопасти на радиусе .

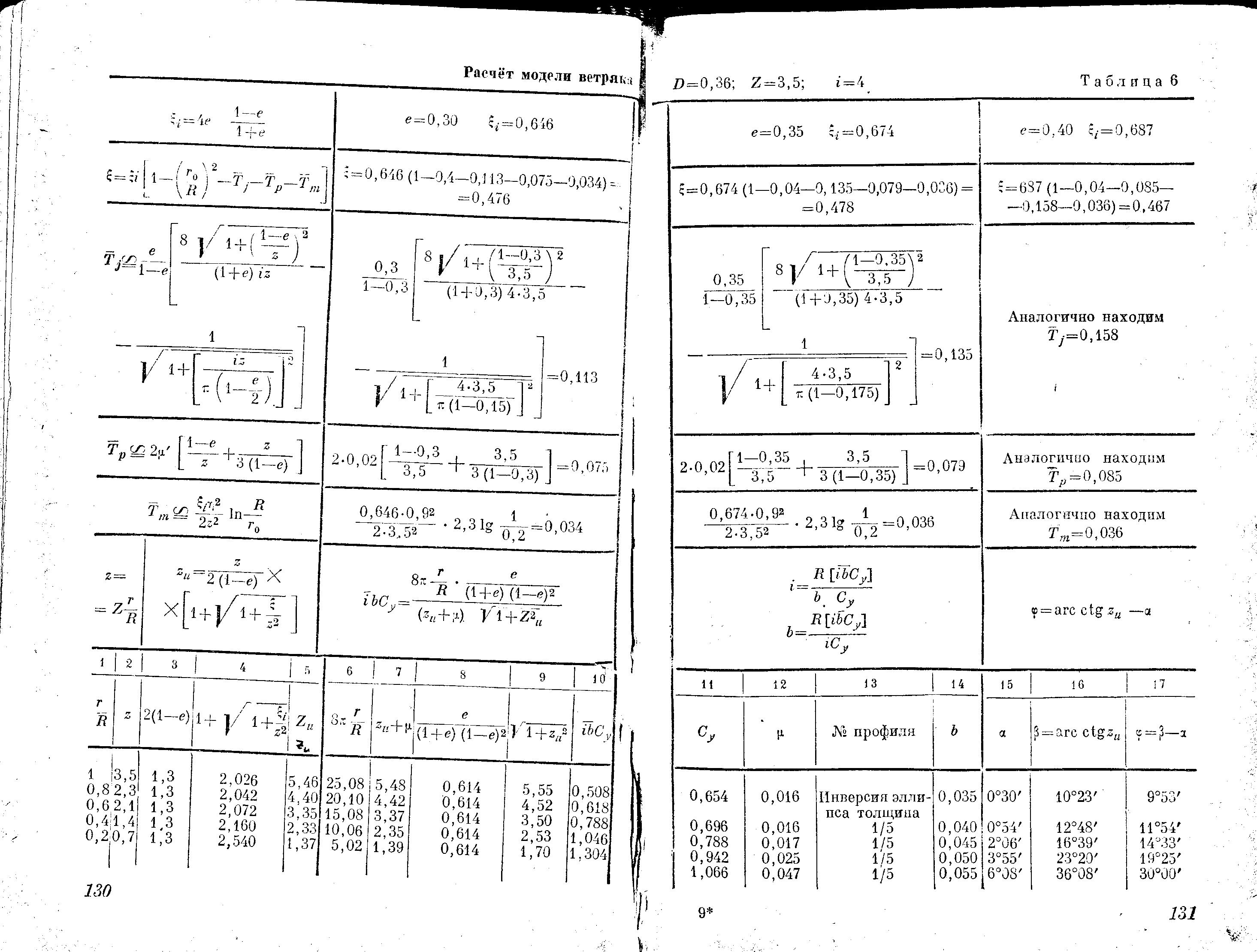
В первой строке вверху помещены частные формулы, по которым ведётся расчёт.

В первых графах 25 вычисляют z_u с помощью фор­мулы (110а); если желательна большая точность, то надо пользоваться уравнением (110). В графах 6­10 подсчи­тывают выражение с помощью формулы (95). В графах 1114 на основании построенной для данного примера диаграммы значений С_у и μ в функции α (рис. 59) вносят значения С_у, μ и b. В графах 15  17 заносят  и вычисляют угол заклинения лопасти φ = β – .

После того как выбран профиль, с помощью диаграммы (рис. 59), устанавливают угол атаки, соответствующий наименьшему μ, и находят С_у.

Задаваясь числом лопастей i, находят ширину лопа­сти: (141)

Найдя значение b, вычисляют окончательное значе­ние C_y: (142)

По диаграмме (рис. 59) находят  и , соответствующие значению С_у, и заносят их в графы 11, 12 и 15 таблицы 6.

Такие же подсчеты проделываются для сечения лопасти r = 0.2. В этом сечении в целях прочности маха принимают более толстый профиль с = от 0,3 до 0,35. И в этом случае С_у выбирают также большим, так как в противном случае ширина лопасти получит чрезмерно большие размеры. Ширина лопасти у втулки берется равной: b_0,2 = 1,3 до 2,0 b₁, (143)

Определив ширину лопасти на конце и у втулки, находят ширину лопасти для любого сечения, принимая её форму в виде трапеции сечения, принимая её форму в виде трапеции: (144)

где: n — число сечений лопасти; k — порядковый номер сечения, считая от конца ло­пасти.

Определив b, находят С_у с помощью уравнения (142), а затем μ и α по графику (рис. 59) и, наконец, φ. Если в результате конструктивной проработки окажется толщина лопасти недостаточной, т. е. мах крыла не по­мещается в контуре профиля, то, увеличивая толщину, необходимо провести расчёт вновь, начиная с 11-й гра­фы таблицы 6.

В этой таблице приведён для примера расчёт модели 4–лопастного ветроколеса D = 0,36 м и с числом модулей Z = 3,5.