18

Теория реального ветряка проф. Г. X. Сабинина работа элементарных лопастей ветроколеса. Первое уравнение связи

Скорость ветра по высоте можно оценить (прогнозировать) по формуле: V = V_o(H/H_o) ^0.14.

Выделим из лопастей ветроколеса двумя концентри­ческими окружностями с радиусами r и r+dr коль­цевую поверхность dF = 2rdr. Это кольцо на крыльях вырежет отрезки дли­ною dr, которые назы­ваются элементарными лопастями (рис.55). Че­рез все точки обеих окружностей проведём линии тока, образую­щие две поверхности ABC, А'В'С' бутылеобразной формы (рис. 56). Жидкость, заключён­ную между этими поверхностями, назо­вём элементарной коль­цевой струёй.

Сделаем предположение, обычно принимае­мое в аналогичных теориях, что разность давлений по обе сторо­ны ветрового колеса, действующая на площадь кольца, получающегося от пересечения ометаемой плоскостью элементарной струи, воспринимается элементарными лопастями.

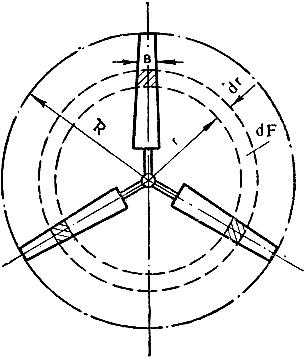
Рис. 55. Выделение элементарных лопастей на ветроколесe. Рис. 56. Элементарная кольцевая струя.

На основании этого составляем первое уравнение связи: 2rdr (ρ₁ – р₂) = n (dY·cos β + dX·sin β), (82)

где: Y — подъёмная сила крыла, направленная перпен­дикулярно потоку; X — сила сопротивления крыла (лобовое сопроти­вление крыла), направленная по потоку, β — угол между плоскостью вращения ветроколеса и направлением воздушного потока, набегаю­щего на крыло; n — число лопастей ветроколеса.

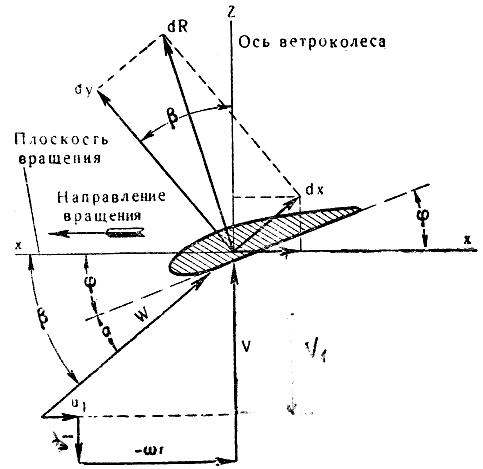
Рис. 57. План скоростей воздушного потока

при набегании его на элемент лопасти.

Для определения направления сил, действующих на элементарную лопасть, изобразим её сечение на рисунке 57, где ось Ζ направлена по оси ветроколеса и ось x — x в плоскости его вращения; V — направление скорости ветра; W — направление скорости относительного потока, набегающего на элемент лопасти.

Разложим силу dR, действующую на элементарную лопасть, на две силы: dX, действующую по потоку, и dY, направленную перпендикулярно потоку. Сила dX вызывает сопротивление элемента крыла; dY вызывает окружное усилие элемента крыла и называется подъём­ной силой.

Вследствие вращения ветроколеса в плоскости x—x воздушный поток набегает на ветроколесо не со скоростью ветра V, а с относительной скоростью W, которая сла­гается геометрически из скорости ветра V и окружной скорости ωr, где ω угловая скорость и r — расстояние элемента лопасти от оси вращения ветроколеса.

Скорость u₁ получается как реакция от крутящего момента, развиваемого лопастями. Эта скорость имеет направление, обратное моменту; её величина берётся как средняя для всей зоны, в которой работают лопасти. В действительности эта скорость перед ветроколесом равна нулю и непосредственно за ветряком равна u₂. Так как закон изменения этой скорости неизвестен, то, как пер­вое приближение, её принимают равной: (84)

Скорость потока, набегающего на элемент лопасти, в относительном движении будет равна: (83)

где V₁ = V – v₁ — скорость ветра в плоскости ветряка.

Силы dY и dX, согласно уравнению (39) § 10, можно выразить так: (85)

(86) , где b — ширина элемента лопасти по хорде.

Кроме того, на основании уравнения (76) можем на­писать: (87)

Подставляя вместо dY, dX и р₁ – p₂ их значения в урав­нение (82), получим:

; (88) после сокращения получим:

(88а)

или

На основании рис. 57 можно ввести обозначение (89)

которое называют числом относительных модулей.

Из уравнения (89) имеем: – r – u₁ = – z_u(V – v₁), или (– r – u₁)² = – z_u² (V – v₁)², и, зная, что V₁=V – v₁ уравнение (83) можем переписать так: (90)

Заменим: (91)

(92)

(93) — обратное качество крыла и подставим их в уравнение (88):

(94)

Вводя в это уравнение е = v₁/V и заменив v₂ его значением из равенства (72), получим:

(95)

Это уравнение называется уравнением связи; оно связывает ширину лопасти и коэффициент подъём­ной силы с деформацией потока, характеризуемой вели­чиной е.

Взяв сумму проекций сил элемента лопасти на каса­тельную к окружности, по которой он движется, получим окружное усилие, развиваемое элементарными лопастями:

Подставляя сюда значение W, sin β и cos β и вводя С_х =  С_у, получим:

(96)

Подставляя сюда значение ibCy из уравнения (95) и сделав сокращения, получим:

(97)

Момент относительно оси ветряка равен: (98)

Секундная работа элементарных лопастей: (99)

Секундная энергия далеко перед ветряком, заключён­ная в потоке, площадь сечения которого определяется площадью кольца, oметаемого элементарными лопастями, равна: . Поделив секундную работу элементарных лопастей на эту энергию, получим элементарный коэффициент использования энергии ветра: откуда: (100)

Умножив и разделив выражение (100) на (1 – е) получим:

Так как выражение представляет идеальный коэффициент использования энергии ветра, то мо­жем написать: (101) где: (102)

называют относительным коэффициентом полезного дей­ствия элементарного ветряка.

При большом числе модулей можно приблизительно считать: и тогда: (102а)

Напомним, что числом модулей, или быстроходностью ветродвигателя, называют отношение окружной скорости конца лопасти к скорости ветра: (59)

Число модулей элементов лопастей на радиусе r равно: (103) Число модулей для любого радиуса r ветряка с извест­ной быстроходностью Ζ может быть выражено так: (104) где R — радиус ветроколеса.