
1. Предмет курса «Прикладная физика». Связь между механикой и физикой. Значение механики для современной техники. Обзор моделей механики. Число степеней свободы. Материальная точка, абсолютно твердое тело, сплошная среда.
Назначение приклада: дать введение в мех. деформ. тв. тела, рассм. инженерные метода расчета и инж. подходу к расчету, дать основу для некоторых дальнейших курсов.
Механика – это искусство построения машин, наука о перемещ. тел в простр. и взаимодействии их друг с другом, техническая наука, явл. частью физики и прикладной математики. Это наука о простейшей форме движ. материи. (u << c). Механич. движ. – изменение с течением времени положения тел отн. друг друга.
Механика делится на: статика, кинематика, динамика. Различают: механику матер. точки; мех. системы мат. точек; мех. абс. тв. тела; мех. сплошной среды; общую мех.; мех. жидкостей и газов; мех. деформируемого тв. тела. Мех. деф. тв. тела включает: теорию упругости, пластичности, ползучести, вязкой упругости, строительную мех., пластин и оболочек, теорию устойч-сти, механику разрушения, мех. композиционных материалов, теорию колебаний упругих систем, теорию надежности, конструкционную точность и т. д., и все это – механика материалов и конструкций - приклад.Модели механики (объект А наз. моделью объекта В, если А отображает наиболее сущ. (с точки зрения данного рассм-я) св-ва объекта В): модель подобия (макет) - объекты имеют одинаковую физ. Природу модель-аналог - имеют разную физ. природу, но опис. аналогич. дифф. ур-ями (колебания) теоретич. модели - теория, гипотеза, расчетная схема, т.е. научная абстракция изуч. Объектов мат. модель – совокуп-ть мат. ур-ий, опис. наиболее существ. св-ва объект.Число степеней свободы – число независ. параметров, кот. однозначно определяют положение всех точек системы (ее конфигурацию) в каждый фикс. момент t.Различают системы: с конечн. числом степ. своб. m, с счетным, сплошные среды (распред, или континуальная система).Мат. точ. – тело, имеет массу, исчезающе малые размеры для данной системы (3 степ. свободы (n = 3)). При налож. связей n может . Одно-сторонние связи: x2 + y2 + z2 l, двусторонние связи: x2 + y2 + z2 = l (для маятника на веревке и стержне).Система мат. Точ. – совокупность мат. точек, движ. и положение которых взаимосвязано (n=3N-s). s граничений. Абсолютное тв. тело – расстояние между двумя любыми точками – неизменно. n = 6 (3 линейных 3 угловых).Сплошная среда – полностью заполняет пространство, молекул. строением пренебрег, расстояние между точками ее может изменяться в процессе движ. Модели сплошной среды: идеальный газ, вязкий газ, ионизир. газ, идеальная несжимаемая жидкость, сжимаем. без трения, вязкая, упругая жидкость, линейно-упругое тв. тело, нелинейное упругое, упругое-пластическое, вязкое-упругое и т. д.
2.
Момент вектора относительно оси и его
свойства. Теорема Вариньона для системы
векторов, сходящихся в одной точке.
Рассмотрим
закрепленный вектор
 и некоторую ось
и некоторую ось
 .
Через точку О на оси
.
Через точку О на оси
 проведем плоскость
проведем плоскость
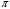 .
Из точки О опустим перпендикуляр на
направление
.
Из точки О опустим перпендикуляр на
направление
 .Опр.
Моментом вектора
.Опр.
Моментом вектора
 относительно оси
относительно оси
 наз-ся произведение модуля
наз-ся произведение модуля
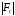 на
длину перпендикуляра r,
опущенного из точки пересечения оси
на
длину перпендикуляра r,
опущенного из точки пересечения оси
 с пл-тью
с пл-тью
 на нап-е век-ра
на нап-е век-ра
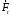 .
.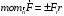 (знак с учетом выбора сист. коорд.)Св-ва
момента вектора отн. заданной оси:1. мом.
вект. отн. зад. оси не зависит от выбора
точки О на оси
(знак с учетом выбора сист. коорд.)Св-ва
момента вектора отн. заданной оси:1. мом.
вект. отн. зад. оси не зависит от выбора
точки О на оси
 2.
При определении мом. вект. отн. зад. оси,
вектор
2.
При определении мом. вект. отн. зад. оси,
вектор
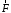 можно
трактовать как скользящий вектор
(сопряж. св-ва).Т.
Вариньона:
Если векторы
можно
трактовать как скользящий вектор
(сопряж. св-ва).Т.
Вариньона:
Если векторы
 сход-ся в одной точке, то момент суммы
векторов
сход-ся в одной точке, то момент суммы
векторов
 может быть определен, как
моментов каждой составляющей:
может быть определен, как
моментов каждой составляющей:
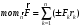 .
.
3.
Момент вектора относительно точки.
Моменты вектора относительно координатных
осей, как составляющие момента вектора
относительно точки. Преобразование
момента относительно полюса. Момент
вектора отн. осей: Представим вектор
 ,
где X, Y, Z
это коорд.
,
где X, Y, Z
это коорд.
 .
.
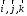 -
единичные орты. Рис. нарисуй (длины
проекций на оси -
-
единичные орты. Рис. нарисуй (длины
проекций на оси -
 ).
Итак, получим ур-ия:
).
Итак, получим ур-ия:
 ;
; ;
; (1),где x, y,
z – длины проекций вектора
(1),где x, y,
z – длины проекций вектора
 на коорд. оси. Момент вектора
отн. точки: Рассм. закрепленный
вектор
на коорд. оси. Момент вектора
отн. точки: Рассм. закрепленный
вектор
 .
.
 – радиус-вектор положения вектора
– радиус-вектор положения вектора
 .
.
 ,
,
 .
Опр. моментом вектора
.
Опр. моментом вектора
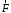 отн. точки (полюса) наз. векторное
произвед. векторов
отн. точки (полюса) наз. векторное
произвед. векторов
 и
и
 :
:
 .
. (2)Сравнивая (1) и (2) можно сделать вывод:
Моменты вектора отн. коорд. осей равны
проекциям момента вектора отн-но начала
коорд. на соотв. оси.Св-ва мом. вектора
отн. полюса:1. Момент вектора отн.
полюса
(2)Сравнивая (1) и (2) можно сделать вывод:
Моменты вектора отн. коорд. осей равны
проекциям момента вектора отн-но начала
коорд. на соотв. оси.Св-ва мом. вектора
отн. полюса:1. Момент вектора отн.
полюса
 ,
если
,
если
 ,
или
,
или
 ,
или
,
или
 .
2. При опр. мом. век-ра отн. полюса в-р
.
2. При опр. мом. век-ра отн. полюса в-р
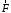 можно трактовать, как скользящий (велич.
мом. не изм., если вектор
можно трактовать, как скользящий (велич.
мом. не изм., если вектор
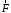 перенести вдоль линии его действия).3.
Преобраз. момента вектора при переносе
полюса.
перенести вдоль линии его действия).3.
Преобраз. момента вектора при переносе
полюса.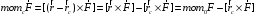 Т.
Вариньона для системы векторов,
сход. в одной точке отн. одного полюса:
Т.
Вариньона для системы векторов,
сход. в одной точке отн. одного полюса:
 .
.
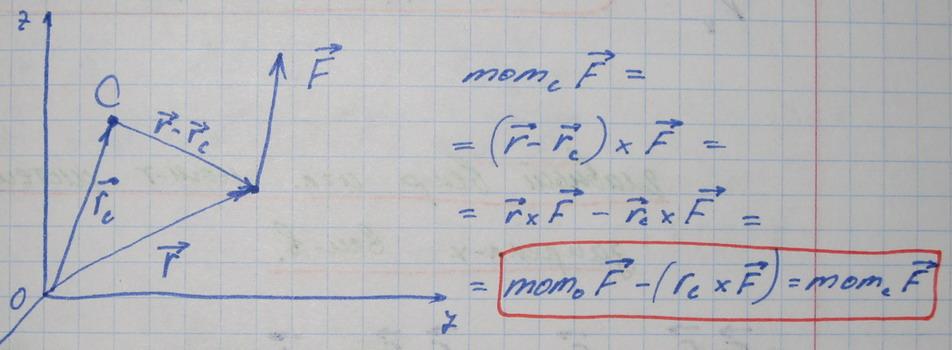

4.
Главный вектор и главный момент системы
закрепленных векторов. Классификация
случаев приведения системы векторов.
Дано
 ,
,
 .
Гл. вект-ом сист. век-ов наз-ся век-р
.
Гл. вект-ом сист. век-ов наз-ся век-р

 - главный вектор.
- главный вектор.
 - главн. момент.1-й инвариант:
- главн. момент.1-й инвариант: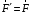 - инв. в др. сист. коорд.
- инв. в др. сист. коорд.
 ;
;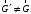 -неинвариант/.2-й
инвариант:скаляр
-неинвариант/.2-й
инвариант:скаляр

 ,
,
 .Приведение
векторов - операция замены сист.
векторов некоторой эквивалентной сист.
состоящей из главного вектора приложенного
к данной точке и главного момента.
.Приведение
векторов - операция замены сист.
векторов некоторой эквивалентной сист.
состоящей из главного вектора приложенного
к данной точке и главного момента.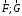 - элементы приведения системы векторов.
Классификация :1.
- элементы приведения системы векторов.
Классификация :1.
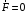 ;
;
 – это справедливо для любой точки
приведения. Система эквивалентна 0.2.
– это справедливо для любой точки
приведения. Система эквивалентна 0.2.
 ;
;
 –
тогда для любой точки приведения
–
тогда для любой точки приведения
 .3.
.3.
 – сущ. Множе-ство точек для которых
– сущ. Множе-ство точек для которых
 .
Говорят, что система сводится к главному
вектору. Геом. место точек для кот.
выполняется условие
.
Говорят, что система сводится к главному
вектору. Геом. место точек для кот.
выполняется условие
 ,
есть – центральная прямая.4.
,
есть – центральная прямая.4.
 при этом не сущ. Множ-во точек для которых
при этом не сущ. Множ-во точек для которых
 .
. Для
любого центра приведения система
сводится к гл. вект. и гл. мом.
Для
любого центра приведения система
сводится к гл. вект. и гл. мом.
 и
и
 .Замечание:
можно выбрать такой центр приведения,
такой центр в пространстве, когда
векторы
.Замечание:
можно выбрать такой центр приведения,
такой центр в пространстве, когда
векторы
 (коллинеарные) (приведение к винту).Условия
при кот. система векторов сводится к
главному вектору:1.
(коллинеарные) (приведение к винту).Условия
при кот. система векторов сводится к
главному вектору:1.
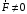 2.
2.
 - взаимно ортогональны.
- взаимно ортогональны.
5.
Аксиомы классической механики. Основные
понятия, входящие в аксиомы. Динамика
материальной точки и системы материальных
точек.Соотношения
между осн-ми понятиями мех-ки опр-я
аксиомами или осн. законами движения,
котор. Сфомулировал Ньютон:1- закон
инерции; 2 -
 ,
,
 - связь силы и ускорения; 3 -
- связь силы и ускорения; 3 -
 .
Принцип
относит-сти Галилея:
Все декартовые системы координат
движущиеся друг относительно друга
равномерно и прямолинейно эквивалентны
между собой с точки зрения определения
сил, действующих на материальное тело.
.
Принцип
относит-сти Галилея:
Все декартовые системы координат
движущиеся друг относительно друга
равномерно и прямолинейно эквивалентны
между собой с точки зрения определения
сил, действующих на материальное тело.
 при
при
 .Сист.
коорд. связанные этим преобразованием
образуют множество инерциальных
систем.Одну из них можно условно
считать неподвижной, т.о. вводится
дополн-й постулат, что сущес-т хотя бы
одна инерциальная сист. отсчёта.Движение
мат. точки в инерциальной системе
координат подчиняется 2-му закону
Ньютона.
.Сист.
коорд. связанные этим преобразованием
образуют множество инерциальных
систем.Одну из них можно условно
считать неподвижной, т.о. вводится
дополн-й постулат, что сущес-т хотя бы
одна инерциальная сист. отсчёта.Движение
мат. точки в инерциальной системе
координат подчиняется 2-му закону
Ньютона.
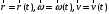 ;
;
 - скорость;
- скорость;
 - ускорение.
- ускорение.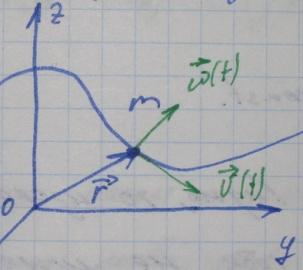
Масса
мат.точки –
одна из основных хар-стик материи, кот.
является мерой её инерц. и гравитац.
свойств. Сила
– мера взаимодействия мат. тела или
мат. тела и поля, приводящая к появлению
ускорения.
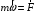 или
или
 или
или
 .Действие
отдельных материальных точек описывается
1-м и 2-м законом Ньютона, действие 2
материальных точек описывается 3-м
законом Ньютона.Основная
задача динамики точки:
состоит в определении равнодей-щей сил
выз-щей заданное движение мат.точки с
известной массой. Задача сводится к
определению ускорения из известных
уравнений движения.
.Действие
отдельных материальных точек описывается
1-м и 2-м законом Ньютона, действие 2
материальных точек описывается 3-м
законом Ньютона.Основная
задача динамики точки:
состоит в определении равнодей-щей сил
выз-щей заданное движение мат.точки с
известной массой. Задача сводится к
определению ускорения из известных
уравнений движения.
 ;
;
 ;
;
 .
Задаются силы, прилож-е к точке:
.
Задаются силы, прилож-е к точке:
 ,
,
 ,
,
 ,
,
 .
Найти
.
Найти
 .
. ,
,
 .
.
 ,
,
 ,
тогда:
,
тогда:
 ,
,
 ,
,
 – дифференциальные
ур-ия движения для мат. точ.Дифф. уравнения
движение системы мат. точек:
– дифференциальные
ур-ия движения для мат. точ.Дифф. уравнения
движение системы мат. точек: –
главный вектор внешних сил,
–
главный вектор внешних сил,
 –главный
вектор внутренних сил.
–главный
вектор внутренних сил.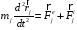 .
.
6. Несвободные системы материальных точек. Связи и их классификация.
Система
свободная – если
на перемещение и скорости всех точек
системы не наложено никаких ограничений
кроме требования конечности и дифф-сти.
Система несвободная
– если наложены какие-либо ограничения
на координаты и скорости, эти ограничения
называются связями.Условия
связи должны выполняться для любых
действующих на систему сил. Каждая связь
определяется одним ур-нием (условием).1.
Связи, условия которых задаются в форме
неравенств, называются односторонними
(неудерживающие).
Дана гибкая нерастяжимая длиной L
нить с координатами концов: и
и
 .
.
 .2.
двухсторонняя
связь .Дан
стержень длиной L,
.2.
двухсторонняя
связь .Дан
стержень длиной L,
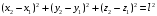 .3.
Связи вида
.3.
Связи вида
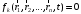 ,
где
,
где
 ;
S
– кол-во связей. В условия связей скорости
мат. точ. не входят, такие точки называют
–
геометрическими.1)
и 2) – геом.4.
;
S
– кол-во связей. В условия связей скорости
мат. точ. не входят, такие точки называют
–
геометрическими.1)
и 2) – геом.4.
 Кинематические
связи –
связи, в условия которых входит скорость.
Кинематические
связи –
связи, в условия которых входит скорость.
 ,
,
 .Возможен
случай когда, ур-ние связи допускает
интеграл
.Возможен
случай когда, ур-ние связи допускает
интеграл
 не содержащий скоростей, тогда совокупность
всех геом. и инегр-мых кинемат. связей
образуют голономные
связи.5.
Связь
стационарна,
если время t
не входит явно в уравнение системы
(связи). В противном случае связь называют
нестационарной.6.
Связь идеальна,
если её
реакции не совершают работы на
перемещениях, совместимых со связями,
в противном случае связь неидеальна.
не содержащий скоростей, тогда совокупность
всех геом. и инегр-мых кинемат. связей
образуют голономные
связи.5.
Связь
стационарна,
если время t
не входит явно в уравнение системы
(связи). В противном случае связь называют
нестационарной.6.
Связь идеальна,
если её
реакции не совершают работы на
перемещениях, совместимых со связями,
в противном случае связь неидеальна.
7. Основные понятия статики. Условия равновесия системы материальных точек.
Рассмотрим
сист. не свободных точек
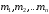 ;
;
 .Движение
системы описывается
.Движение
системы описывается
 .
. - главный вектор всех активных сил,
- главный вектор всех активных сил,
 -
главный вектор всех реактивных сил,
прилож. к j
– ой массе. Активные силы – заданы,
реактивные – надо найти.Опр.
мат. точка нах. в
равновесии,
если равен нулю главный вектор всех
активных и реактивных сил
-
главный вектор всех реактивных сил,
прилож. к j
– ой массе. Активные силы – заданы,
реактивные – надо найти.Опр.
мат. точка нах. в
равновесии,
если равен нулю главный вектор всех
активных и реактивных сил
 .
.
Сист.
мат. точек нах. в равновесии,
если каждая ее точка нах. в равн.Опр.
сист. нах. в
покое, если
все ее точки неподвиж.Теорема:
если сист. нах. в равновес., то и любая
ее подсистема тоже нах. в равн.Теорема:
если сист. нах. в равн, то все ее точки
совершают равномерн. прямолин. движ.
отн. инерц. сист. коорд.Состояние
равновесия
– динамич. хар-ка, сост.
покоя –
кинематич. хар-ка (понятия отождетв. при
0-вых нач. усл.).Необх.
усл. равновес. сис. мат. точек т.
здесь много ф-ул и преобраз, все они
рассм. все силы для кажд. точки 1, …, N.В
итоге получ. условие:
 ,
где
,
где
 - главный вектор всех внешних активных
и реактивных сил, прилож. к системе.Итак:
1.
необх. усл.:
- главный вектор всех внешних активных
и реактивных сил, прилож. к системе.Итак:
1.
необх. усл.:
 ,
или
,
или
 ,
,
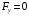 ,
,
 .Теорема:
Если сист. нах. в равн., то главный вектор
всех внешних активных и реактивных сил,
прилож. к системе = 0.2.
необх. условие.
равенство нулю гл. момента всех внеш.
сил
.Теорема:
Если сист. нах. в равн., то главный вектор
всех внешних активных и реактивных сил,
прилож. к системе = 0.2.
необх. условие.
равенство нулю гл. момента всех внеш.
сил

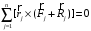 .
Разложи для каждой точки сист., получишь,
что все члены, содержащ. моменты внутр.
сил взаимоуничтож.
.
Разложи для каждой точки сист., получишь,
что все члены, содержащ. моменты внутр.
сил взаимоуничтож. ,
или
,
или
 ,
или
,
или
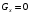 ,
,
 ,
,
 ,
или
,
или
 ,
,
 ,
,
 .
Теорема:
если сист. нах. в равновес., то главный
момент всех внеш. активных и реактивн.
сил отн. произвол. полюса = 0.
.
Теорема:
если сист. нах. в равновес., то главный
момент всех внеш. активных и реактивн.
сил отн. произвол. полюса = 0.
8. Необходимые условия равновесия абсолютно твёрдого тела.
(они же и достат.). n = 6. Эти условия F = 0, G = 0. Абс. тв. тело нах. в равн. тогда и только тогда, когда главн. вектор и главн. момент всех внешн. активн. и реакт. сил = 0. Т. равновес. АТТ не наруш, если действ. на него силы перенести по линии их действия (скользящ. векторы), но это утв. может быть ошибочно при кол-ве тел в сист. 1.Частные случаи: сист. сход. сил (в одну точку): G = 0 (всегда), условие: F = 0. Парралельн. сист. сил. Fj || OZ. Тогда условия: Fx = 0, Gx = 0, Gy = 0. Плоская сист. сил: Fj OХY. Тогда условия Fy = 0, Fz = 0, Gx = 0. Модификац.: плоская сист. сил, сход. в 1-ой точке: условия: Fy = 0, Fz = 0. плоская || сист. сил: условия: Fy = 0, Gx = 0. Система из N АТТ: n = 6N – s в R3, и 3N – s в R2. Классификац. сист. АТТ. Системы с n 1 наз. геометрич. изменяемыми или механизмами. Сист. с n = 0 наз. конструкциями или структурами. Сист., реакц. внеш. и внутр. связей в котор. можно найти, используя лишь ур-ия статики, наз. статически определимыми. Обобщенная система коорд. отлич. от ДСК тем, что ДК явл. независ, а ОК связаны с учетом связей (???). ОК не обяз. иметь четкий геометрич. смысл.
10. Принцип Даламбера для сист. матер. точек. Общее ур-е динамики Даламбера-Эйлера. Распространим ПВП на случ. движения сист. Ур-ия динамики мех. сист. формально сосвадают с уравн. равновес. этой сист., если к действит. внеш. силам, внутр. силам и реакц. связей добавить фиктивные (Даламберовы) силы инерции. Fj(i) + fj(i) + Rj + Ij = 0, j = 1, 2, …, N, Ij = - mj(d2r/dt2). Движ. сист. происх. так, что в любой момент t работ всех внеш. и внутр. сил, реакц. связей и даламберовых сил на любых виртуальн. перем. = 0. Итак, самое Общее ур-е динамики Даламбера-Эйлера: j=1N(Fj + Fj + Rj + + Ij)rj = 0, j = 1, 2, …, N. Н. Е. Жуковский: "Если в некотор. момент. t остановить систему и вместе с тем приложить к ее точкам силы инерции не изменяя активные силы, то сист. будет находиться в равновесии и реакции связей останутся такими, какими они были во время движения".
9. Понятие о виртуальных перемещениях. Формулир-ка принц. вирт. перем. Принцип вирт. перем. для сист. с идеальн. связями. Вирт. или возможными перемещ. наз. любая совокупность малых перемещ. точек… При этом не треб. удовл. ур-ям движ. rj~ = rj + rj. fk(r1, r2, …, rN; t) = 0, k = 1, 2, …, s. (1), fk(r1~, r2~, …, rN~; t) = 0, k = 1, 2, …, s. (2). Движ. rj отлич. от действ. малых движ. drj, котор. удовл. ур-ию и (1), и (2). rj - только (2). Принцип вирт. перемещ.: будем рассм. сист. со стационарн. связями, а также предполагаем, что активн. силы явно от времени не зависят. j=1N(Fj + Rj)rj = 0, j = 1, 2, …, N (3). Равнство (3) выражает ПВП. Это рав-во заменяет всю геометтрич. статику. Известоно, что Fdr = d'A (d'A – действит. элементарная работа (не явл. полным дифф.), по аналогии Fr = 'A – вирт. работа силы F на вирт. перемещ. r. Сист. с двухсторонними связями нах. в равновес. тогда и только тогда, когда вирт. работ всех активн. и реакт. сил на любых вирт перемещ. = 0. ПВП для сист. с идеальн. связями. Связь наз. идеальн., если работа реакции на любых ВП = 0. Rjrj = 0. j=1NFjrj = 0, j = 1, 2, …, N. (4). Важным св-вом сил реакции связей явл. то, что их полная работа при малом отклонении системы от полож. равн. =0. Применение ПВП к АТТ. Рассм. абс. тв. свободное тело, на котор. действ. F1, F2, …, FN. Если сист. нах. в равн., то сист. удовл. ур-ию j=1NFjrj = 0, j = 1, 2, …, N. Т. Шаля: Всякое перемещ. свободного АТТ из одного полож в другое может быть получено посредством поступательного и вращат. движений. rj = r0 + [ x rj], (5). rj - радиус-вектор j – ой точки, r0 - вектор поступат. перемещ., - вектор вращения отн. какого либо полюса. Подставим (5) в (4). j=1N[rj x Fj] = 0 G = 0. Отсюда след, что взятые в . слагаемые должны обращ. в 0, т. к. r0 и явл. независ. Замеч.: ПВП дает необх. и достат. усл. равновес. сил в каждой точке матер. сист. и в то же время необх. но недостат. усл. равн. для всей сист. целом. Для АТТ эти усл. будут и достат.
11.Общие предположения о свойствах материалов. Внешние и внутренние силы. Метод сечений.Нас будет интересовать не отдельные частицы, поведение материала как целого. Реальное тело(вещ-во) заменяем некоторым идеальным (моделью). В дальнейшем – модель сплошной среды.
Применяемые гипотезы: 1)о сплошности 2)об однородности 3)об изотропности 4)о жесткости 5)о линейности
Внешние силы. Классификация Наиболее существенные признаки:1)-место расположения точек приложения сил
2)по характеру изменения сил в процессе их приложения.
Внутренние
силы. Метод сечений
В общей
механике была введена аксиома связи. В
механике деформирующегося тела введем
понятие внутренних связей, т.е. связей,
обеспечивающих целостность тела.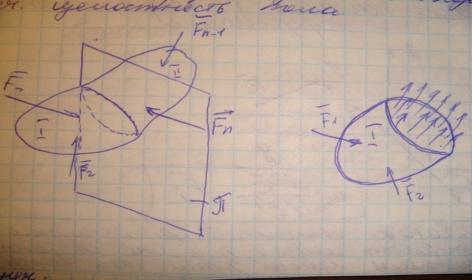
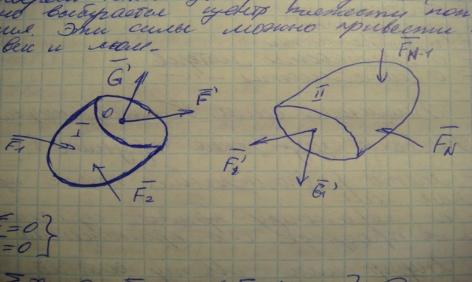
Прием,
позволяющий перенести внутренние силы
в разряд внешних, называется методом
сечений. Выберем некоторый центр
приведения(полюс). Обычно выбирается
центр тяжести поперечного сечения. Эти
силы можно привести к главному вектору
и моменту. =0;
=0; =0
∑x=0;∑y=0;∑z=0
momx=0;momy=0;momz=0
=0
∑x=0;∑y=0;∑z=0
momx=0;momy=0;momz=0
12.Тензор
напряжений. Симметрия тензора напряжений.
Связь между тензором напряжений и
вектором напряжений по произвольной
площадке, проведенной через данную
точку.Нормальные и касательные
напряжения на взаимно ортогональных
площадках.Казалось бы, что для полной
характеристики напряженного состояния
 1=
1=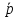 n1;
n1; 2=
2= n2;
n2; k=
k=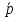 nk
nk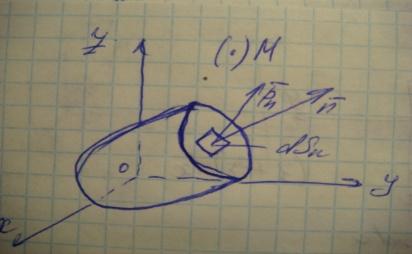

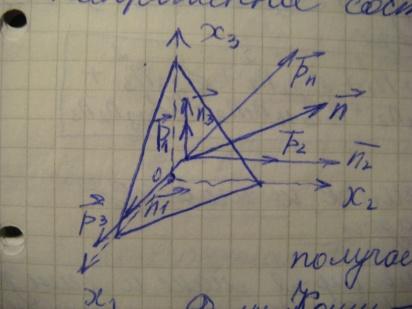
Представим
вектор
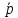 x
в виде разложения:
x
в виде разложения:
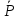 x=σxx
x=σxx +σxy
+σxy +σzx
+σzx

 y=σxy
y=σxy +σyy
+σyy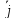 +σzy
+σzy =>
=>
 z=σxz
z=σxz +σyz
+σyz +σzz
+σzz
Эта
матрица соответствует некоторой
тензорной величине и называется тензором
в данной точке.σxx;σyy;σzz
– нормальные напряжения. Остальные -
касательные напряжения, они равны.
Первый индекс – ось действия, второй –
направление нормали к площадке, по кот.
действуют эти напряжения. Четкий
механический смысл приведенное правило
имеет только для растяжения/ сжатия.
Компоненты тензора напр. На площадке с
отрицательной внешней нормалью считаются
положительными, если они направлены в
сторону, противоположную соотв. оси.
Симметрия тензора напряжения (Закон
парности).Тензор напряжения является
симметричным: σjk =
σkj. Для доказательства
закона парности необходимо составить
уравнения равновесия статики для
элемента с действующими на него
напряжениями на площадках с положит. и
отриц. нормалями. F=σS.Связь:
Через произвольную точку сплошной среды
можно провести множество площадок, по
которым действуют различные напряжения
Pj.
Задание тензора напряжений в данной
точке позволяет вычислить вектор
напряжения Pj
, действующий по любой площадке с нормалью
 j
, проходящей через данную точку. Если
задан
j
, проходящей через данную точку. Если
задан
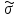 ,
то можно определить напряженное состояние
точки. Составляя уравнения статики
для выделенного, получаем
,
то можно определить напряженное состояние
точки. Составляя уравнения статики
для выделенного, получаем
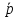 1=σ11n1+σ12n2+σ13n3
1=σ11n1+σ12n2+σ13n3
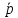 2=σ21n1+σ22n2+σ23n3
2=σ21n1+σ22n2+σ23n3
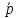 3=σ31n1+σ32n2+σ33n3
- Формулы Коши
3=σ31n1+σ32n2+σ33n3
- Формулы Коши
 j=σjknk
;
j=σjknk
;
 j=
j= Формулы Коши выражают напряженное
состояние в точке полностью определенно,
если заданы нормальные и касательные
напряжения (тензор) по трем взаимно
перпенд. площадкам, проведенным через
эту точку.Нормальные напряжения,
действующие на каждую площадку.Вектор
Формулы Коши выражают напряженное
состояние в точке полностью определенно,
если заданы нормальные и касательные
напряжения (тензор) по трем взаимно
перпенд. площадкам, проведенным через
эту точку.Нормальные напряжения,
действующие на каждую площадку.Вектор
 nn
нормального напряжения, действующего
по наклонной площадке определим как
сумму проекций векторов p1,p2
и p3 на направление
нормали
nn
нормального напряжения, действующего
по наклонной площадке определим как
сумму проекций векторов p1,p2
и p3 на направление
нормали
 .pnn=p1n1+p2n2+p3n3
подставим в эту формулу формулы
Коши и учтем, что σjk=σkj
тогда:
.pnn=p1n1+p2n2+p3n3
подставим в эту формулу формулы
Коши и учтем, что σjk=σkj
тогда: nn=σ11n12+σ22n22+σ33n33+2σ12n1n2+2σ13n1n3+2σ23n2n3
nn=σ11n12+σ22n22+σ33n33+2σ12n1n2+2σ13n1n3+2σ23n2n3

Гл
напряжение и главные площадки.Для
определения макс и мин значения напряжения
pnn
применим метод неопределенных множителей
Лагранжа. Задача отыскания относительного
экстремума.n12+n22+n32=1
, используя необходимое условие
экстремума( равенство нулю частных
производных) получаем систему однородных
уравнений:(σ11-σ)n1+σ12n2+σ13n3=0
σ21n1+(σ22-σ)n2+σ23n3=0
σ31n3+σ32n2+(σ33-σ)n3=0
эта сист. имеет решение, ежели
определитель равен 0. Получаем кубическое
относительно σ уравнение, которое
подчиняется след.правилу присвоения
индексов: σ1 σ2
σ2 σ3
Площадки, по которым действуют эти
напряжения, назыв. главными. На них
касательные напряжения = 0. Механ.
истолкование главных напряжений.В
каждой точке сплошной среды существуют
3 взаимно перпенд. площадки, по которым
действуют только нормальные напряж..
Напряж. состояние в окрестности любой
точ. можно представить как растяжения
в 3 взаимно перпенд. направлениях,
совпадающих с направлен. нормалей к
главным площадкам.Элипсоид Ламе
Радиус-вектор произвольной точ. такой
пов-сти представл.полное напряжение на
одной из площадок, положение кот. определ.
Велич. М1,М2,М3. При этом
одно из гл. напряж. явл. макс, другое мин.
Инварианты тензора. Разложение
тензора . на сфер. тензор и девиатор. Гл.
напряж., как и все напряж. состояния в
данной точ. зависят от нагрузок и не
зависят от выбора корд. осей =>и при
других исходных напряжениях получаем
одно и тоже кубическое уравнение =>
коэф-ты и свободные члены ур-ия инвариантны
к преобразованию координат и называются
инвариантами тензора напряжений в этой
точке.I1=σ11+σ22+σ33
I’1=σ1+σ2+σ3
σ3
Площадки, по которым действуют эти
напряжения, назыв. главными. На них
касательные напряжения = 0. Механ.
истолкование главных напряжений.В
каждой точке сплошной среды существуют
3 взаимно перпенд. площадки, по которым
действуют только нормальные напряж..
Напряж. состояние в окрестности любой
точ. можно представить как растяжения
в 3 взаимно перпенд. направлениях,
совпадающих с направлен. нормалей к
главным площадкам.Элипсоид Ламе
Радиус-вектор произвольной точ. такой
пов-сти представл.полное напряжение на
одной из площадок, положение кот. определ.
Велич. М1,М2,М3. При этом
одно из гл. напряж. явл. макс, другое мин.
Инварианты тензора. Разложение
тензора . на сфер. тензор и девиатор. Гл.
напряж., как и все напряж. состояния в
данной точ. зависят от нагрузок и не
зависят от выбора корд. осей =>и при
других исходных напряжениях получаем
одно и тоже кубическое уравнение =>
коэф-ты и свободные члены ур-ия инвариантны
к преобразованию координат и называются
инвариантами тензора напряжений в этой
точке.I1=σ11+σ22+σ33
I’1=σ1+σ2+σ3
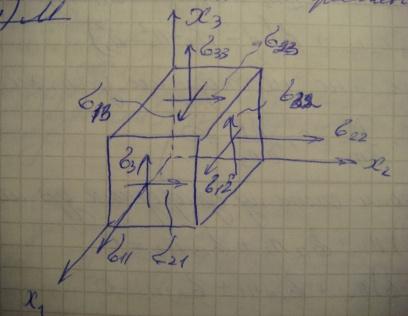

13.Линейные и угловые деформации. Тензор деформации. Геометрич. истолкование компонент ТД. Рис.: оси xyz, на них кубик dV = dxdydz. Рис.2: оси только х и у, на них квадратик dydx (начальное сост.). На расстоянии u по x и U по y тот же кубик, но уже ромбик. Его стороны dx + (u/x)dx; dy + (U/y)dy, отклонение верт. стороны на угол , горизонт. на , левый нижн. угол (/2) - ху, отклонение вертикальной стороны от вертикали (U/y)dy, горизонт. стороны от горизонтали – (u/x)dx. Учитывая гипотез. о малости деформаций, получаем td ,tg .Тогда x=(dx + (u/x)dx – dx)/dx = u/x. ху + = u/y + U/x. Получаем соотн. Коши: x = u/x. y = u/y. z = u/w. ху = u/y + U/x. ху = u/z + w/x. ху = U/z + w/y. ТН модно представить в виде симметричного тензора 2-ого ранга. при условии, что ху = ½ху~ + ½ух~. Итак, ТД: = (хх, xy, xz; yx, yy, yz; zx, zy, zz). ТД обладает теми же св-вами что и ТН и полностью определяет деформир. сост. тела. Все ф-лы одинаковы. Относит. изменение объема: = V/V = ((dx + xdx)(dy + ydy)(dz + zdz) – dxdydz)/dxdydz = (dxdydz + (x + y + z)dxdydz + xyzdxdydz + + dxdydz)/dxdydz = x + y + z (т. к. ~ 10-3 … 10-5). Итак, = V/V = x + y + z = I1 - первый инвариант ТД. Если I1 = = 0, это означ., что деформ. не сопровожд. изменением объема. ТД может быть представлен в виде: = Sph + Dev. Ур-ия неразрывности деформации. Соотн. Коши связывают 6 ф-ий коорд. с 3-мя ф-иями перемещ. (u, U, w). Исключим из соотн. Коши u, U, w: x = u/x. y = u/y. z = u/w. (2/y2)(x) + (2/x2)(y) = (2/y2)(u/x) + (2/x2)(u/y) = 3u/xy2 + 3U/yx2 = (2/xy)(u/y + U/x). Получ. тождества Сенвенана: (2/y2)(x) + (2/x2)(y) = (2/xy)ху; (2/z2)(y) + (2/y2)(z) = (2/yz)yz; (2/z2)(x) + (2/x2)(z) = (2/xz)хz.
14. Закон Гука при растяж. / сжатии. Закон Гука при сдвиге. Обобщенный закон Гука. Связь межу объемным модулем, модулем Юнга и коэфф. Пуассона. Упругость – св-во тел восстанавливать первонач. размеры после снятия внеш. нагрузок. Правельнее говорить не о хрупких или пластичных матер. а о хрупком и пластичном состояниях в-ва. Количественно, упругость выраж. в том, что компоненты тензора напряж. явл. однозначными ф-ями тензора деформации, которые универсальны для данного материала и не зависят от порядка следования деформации, т. е. jk = Ф(jk). Объемный закон Гука. Закон Гука при сдвиге. Материалы по разному ведут себя по отношению к объемной деформации или к сдвигу. Sph = 3Kph. Dev = 2GDev. Или = K, = G. К – объемный модуль упругости, G – модуль сдвига. (справедливы для изотропн. мат.). Закон Гука при растяж. / сжатии. Рис. стержень, растяг. силой Р, первоначально / после деформ.: длина l / l + l; диаметр b / b + b. Вычислим отн. лин. деформации: = l/l; ' = b/b. = '/ - коэфф. Пуассона. Закон Гука: = Е, Е – модульупругости (модуль Юнга). Е, достаточно легко вычисл. из опыта на растяж/сжатие. х = x(x) + x(y) + x(z) = x/E + (- y/E) + (- z/E) = (1/E)(x - (y + z)). Итак, ОЗГ: х = (1/E)(x - (y + z)), y = (1/E)(y - (x + z)), z = (1/E)(z - (x + y)). = G - для сдвига, xy = xy/G; xz = xz/G; yz = yz/G. это тоже ОЗГ. Для изотроп. материала эти 3 константы Е, , G не явл. независ: G = E/(2(1 + )). Связь межу объемным модулем, модулем Юнга и коэфф. Пуассона. Введем среднее или гидростатич. давление: = (1/3)(x + y + z). Знаем, что = x + y + z = (1/Е)(x + y + z - 2(x + y + + z)) = ((1 - 2)/Е)(x + y + z). = K = /К, ((1 - 2)/Е)(x + y + z) = (3(1 - 2)/Е)((x + y + z)/3) = = (3(1 - 2)/Е) = . К = Е/(3(1 - 2)). Вообще: 0 (из термодинамич. сообр, иначе вечн. двигат.) К ,0 ½. Для каучука ½, для пробкового дерева 0.
15. Испытания на растяж. Основные механич. хар-ки конструкционных материалов. Опыт на растяж – это почти единств. возм. осущ. однород. напряж. сост. Образец – на нем риски, Ø 10мм. График.: оси и , график растяжения.Основные точки:пц – предел пропорциональности, т – площадка текучести, в – предел прочности - макс. , разруш. Линии Чернова-Люберса, есть следы выхода дислокаций на пов-ть. 2-е хар-ки: относительное сужение после разрыва: = ((lk – l0)/l0)*100%. Относит. сужение после разрыва: = ((Fk – F0)/F0)*100%. Все условно, т. к. отнесено к F0, d0. Эффект Баушингера. Два графика. после разгружения переходим в точку О'. Повторное нагруж. происх. по линии О'К. Теоретич. прочность. Если считать структуру материала идеальной, то в этом случае прочность его была-бы на 2…3 порядка выше. Такое расхожд. объясняется наличием дислокаций – деффектов КР.Их плотность может достигать 107…108 см/см3 [длина дислокац./объем]. Различные факторы, оказ. влияние на прочность: вид материала, форма и размер тела, протяженность нагружения (деформирования), число циклов нагрузки, t, скорость нагрузки, степень агрессивности окруж. среды, внешнее излучение и др. некотор. переходная зона изменения указ. параметров, котор. разделяет область пластич. разруш. от хрупкого. Эксплуатац. констр. в области хрупкого разр. недопустима. Факторы, вызыв. охрупчивание: содерж. С в мат, близость напряж. сост. к всестороннему равномерн. нагруж., термообработка, увеличение габаритов конструкции (масштабный фактор), концентрац. напряжений, t окруж. среды,радиоакт. Излуч.
16. Основы теории прочности. Общие
понятия о критериях предельных состояний.
Критерий текучести Треска – Сен-Венана
и критерий Губера–Мизеса. Критерий
Мора. Запись критериев текучести для
упрощенного плоского напряж. Сост..На
практике трудно исследовать объёмное
напряж. сост. Для облегчения проверки
системы на прочность вводится некот.
ф-ция
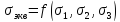 ,
исследуя кот. можно сделать вывод о
напряж. сост. системы в целом, сравнив
её значение с тем значением, при котором
в данной точке напряж. тела наступает
предел. сост.. Предельное сост.Пластич.
материал:
,
исследуя кот. можно сделать вывод о
напряж. сост. системы в целом, сравнив
её значение с тем значением, при котором
в данной точке напряж. тела наступает
предел. сост.. Предельное сост.Пластич.
материал:
 .
Хрупкий материал:
.
Хрупкий материал:
 .
Физич. условие прочности:
.
Физич. условие прочности:
 (пластич. мат.),
(пластич. мат.),
 (хруп. мат.).Технич. условие прочности:
(хруп. мат.).Технич. условие прочности:
 (пласт.),
(пласт.),
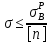 (хруп.)
(хруп.)
 – нормат. коэфф. запаса прочности.
– нормат. коэфф. запаса прочности.
 – фактич. коэфф. запаса прочности.Рассмотрим
пространство главных напряжений
– фактич. коэфф. запаса прочности.Рассмотрим
пространство главных напряжений
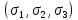 .
В нём сущ. некая область допустимых
сост. такая, что при попадании конца
вектора главных напряжений за границу
этой области наступает предельное
состояние. Таким образом, можно составить
уравнение пов-сти текучести
.
В нём сущ. некая область допустимых
сост. такая, что при попадании конца
вектора главных напряжений за границу
этой области наступает предельное
состояние. Таким образом, можно составить
уравнение пов-сти текучести
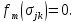 Исходя из механич. соображений, делается
предположение о причине разрушения
материала. Эта причина считается
одинаковой для всех возможных напряж.
состояний. Такой фактор имеет чисто
механич. природу и может быть оценен
качественно (напряжение, деф-ция,
энергия).Критерий текучести Треска–
Сен-Венана.Опыт показывает, что
разрушения предшествуют большие
остаточные деф-ции,а также,что
ответственными за наступление текучести
являются касат. напряжения.Текучесть
наступает тогда, когда наибольшее касат.
напряжение достигает предел. значения,
не зависящего от вида напряж. состояния,
а зависящего только от св-тв материала.Таким
образом, условием наступления текучести
является
Исходя из механич. соображений, делается
предположение о причине разрушения
материала. Эта причина считается
одинаковой для всех возможных напряж.
состояний. Такой фактор имеет чисто
механич. природу и может быть оценен
качественно (напряжение, деф-ция,
энергия).Критерий текучести Треска–
Сен-Венана.Опыт показывает, что
разрушения предшествуют большие
остаточные деф-ции,а также,что
ответственными за наступление текучести
являются касат. напряжения.Текучесть
наступает тогда, когда наибольшее касат.
напряжение достигает предел. значения,
не зависящего от вида напряж. состояния,
а зависящего только от св-тв материала.Таким
образом, условием наступления текучести
является
 .
Для одномерного напряж. состояния
.
Для одномерного напряж. состояния
 .
Тогда
.
Тогда
 .
Для объемного напряж. Сост.
.
Для объемного напряж. Сост.
 .
.
 .Критерий
текучести Губера–Мизеса.
Текучесть наступает тогда, когда
плот-ть потенц. энергии деф-ции девиатора
достигает предел. значения, не завис.от
вида напряж.сост.,а завис-го только от
св-тв материала.
.Критерий
текучести Губера–Мизеса.
Текучесть наступает тогда, когда
плот-ть потенц. энергии деф-ции девиатора
достигает предел. значения, не завис.от
вида напряж.сост.,а завис-го только от
св-тв материала.
 .Критерий
Мора. Предельное состояние
(разрушение) наступает тогда, когда
точка, соответствующая данному
напряженному состоянию выйдет за пределы
области, полученной по результатам
частных и предельных случаев.
.Критерий
Мора. Предельное состояние
(разрушение) наступает тогда, когда
точка, соответствующая данному
напряженному состоянию выйдет за пределы
области, полученной по результатам
частных и предельных случаев.
 ,
,
 – безразмерная хар-ка хрупкого
материала.
– безразмерная хар-ка хрупкого
материала. Запись
критериев текучести для упрощенного
плоского напряж.состояния.
Запись
критериев текучести для упрощенного
плоского напряж.состояния. .
.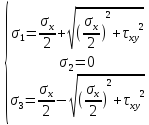 Обозначим
Обозначим
 ,
,
 .
Критерий Сен-Венана:
.
Критерий Сен-Венана:
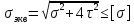 .
.
Критерий Мизеса:
 .
Критерий Мора:
.
Критерий Мора:
 .
.
17. Общие вопросы надежности конструкций
и элементов энергофизического
оборудования. Прочность, жесткость,
устойчивость элементов конструкций.
Допускаемые напряжения и коэффициент
запаса прочности. Механика материалов
и конструкций – наука о расчёте машин,
конструкций и их элементов на прочность,
жесткость и устойчивость. Надежность
– комплексное свойство технического
объекта (прибора, устройства, машины,
системы), заключающееся в его способности
выполнять заданные функции, сохраняя
свои основные характеристики (при опред.
условиях эксплуатации) в установленных
пределах. Понятие надёжности включает
безотказность, долговечность,
ремонтопригодность, сохраняемость,
живучесть, и т.д. Безотказность
– свойство изделия сохранять
работоспособность в течение некоторого
времени или вплоть до выполнения
определенного объема работы без
вынужденных перерывов в заданных
условиях эксплуатации.Прочность
– способность конструкции сопротивляться
действию внешних нагрузок и др. воздействий
(температура, смещений опор, …) не
разрушаясь. Жесткость: если
в процессе нагружения изменения размеров
и форм незначительны и не приводят к
нарушению эксплуатационных свойств,
то говорят, что конструкция обладает
необходимой жесткостью. Устойчивость:
если усилия приводят к малым и исчезающим
после снятия воздействия отклонениям,
то такое состояние равновесия называется
устойчивым. Расчёт этих трёх параметров
служит обеспечением механической
надежности. В общем случае для пластических
материалов условие прочности записывается
следующим образом:
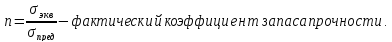
Необходимость введения нормативного коэфф. запаса обусловлена следующими факторами:1)неполная достоверность сведений о величине и характере внешних нагрузок.2)наличие разброса механических свойств материала.3)несовершенство расчётной схемы.4)несовершенство изготовления, монтажа, условий работы.
Кроме того,
 учитывает назначение, степень
ответственности, срок эксплуатации, и
т.д.
учитывает назначение, степень
ответственности, срок эксплуатации, и
т.д.
18. Принцип Сен-Венана. Понятие о
концентрации напряжений. На достаточном
расстоянии от места приложения системы
сил статически эквивалентных
нулю напряжения деформации в упругом
теле, вызываемые этой системой сил,
равны нулю. Система
сил, прилож. к телу, должна быть распределена
по достаточно по сравнению с характер.
размерами тела Фундамент. следствие из
этого прин-ципа:если силы приложены на
малом по сравнению с характер. размерами
тела участке, то напряж. деформир. сост.
на достаточном удалении от места
приложения системы сил полностью
определяется статическим эквивалентом
данной сист. сил. Поня-тие о концентрац.
напряжений.Имеется широкий
класс задач,к кот. принцип Сен–Венана
неприменим. Это связано в основном с
наличием концентраторов напряжений.Концентрация
напряжений–локальное отклонение
однородных полей напряжений вблизи
окрестности резких изменений формы и
размеров тела, а также в окрестности
площади нагружения.
Система
сил, прилож. к телу, должна быть распределена
по достаточно по сравнению с характер.
размерами тела Фундамент. следствие из
этого прин-ципа:если силы приложены на
малом по сравнению с характер. размерами
тела участке, то напряж. деформир. сост.
на достаточном удалении от места
приложения системы сил полностью
определяется статическим эквивалентом
данной сист. сил. Поня-тие о концентрац.
напряжений.Имеется широкий
класс задач,к кот. принцип Сен–Венана
неприменим. Это связано в основном с
наличием концентраторов напряжений.Концентрация
напряжений–локальное отклонение
однородных полей напряжений вблизи
окрестности резких изменений формы и
размеров тела, а также в окрестности
площади нагружения.
19. I)Конструкции,
работающие на растяжение (сжатие). Осевая
деформация прямолинейного стержня.II)Работа
внешних сил и потенциальная энергия
упругой деформации или
растяжения(сжатия).I)Рассмотрим
осевую деформацию стержней с криволинейной
осью, такая деф-ция возможна, когда
внешние нагрузки сводятся к главному
вектору.
 При этом линия действия главного вектора
совпадает с направлением продольной
оси стержня, центральное напряжение.При
изучении осевой деф-ции прямого стержня
есть гипотезы:1)гипотеза плоских сечений-
сечения плоские по деф-ции остаются
плоскими и паралел. Друг другу и после
деф-ции.2)закон Гука
При этом линия действия главного вектора
совпадает с направлением продольной
оси стержня, центральное напряжение.При
изучении осевой деф-ции прямого стержня
есть гипотезы:1)гипотеза плоских сечений-
сечения плоские по деф-ции остаются
плоскими и паралел. Друг другу и после
деф-ции.2)закон Гука
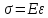 3)о ненадавливании волокон
3)о ненадавливании волокон

 .
. и
и
 можно
пренебрегать Nz=
можно
пренебрегать Nz= .
σ=const
σ=(Nz)/F.
.
σ=const
σ=(Nz)/F.
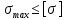
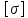 =
= пред/[n].
II)Материал
линейно упругий,внешние силы прикла-дываются
квазистатически, перемещение точек
тела малы, потери энергии на трение,
перемагнич. малы. A=0.5P*
пред/[n].
II)Материал
линейно упругий,внешние силы прикла-дываются
квазистатически, перемещение точек
тела малы, потери энергии на трение,
перемагнич. малы. A=0.5P* dU=dA=0.5Nz(
dU=dA=0.5Nz( .U=0.5
.U=0.5 -общий
случай. В случае если Nz
и EF
-const
U=0.5
-общий
случай. В случае если Nz
и EF
-const
U=0.5 .
При вычислении потенц. Энергии упругой
деф-ции принцип суперпозиции неприменим
и нелинейно относится Nz
.
При вычислении потенц. Энергии упругой
деф-ции принцип суперпозиции неприменим
и нелинейно относится Nz


20. Интеграл
Максвелла-Мора для случая растяжения(сжатия).
Определения взаимных и температурных
перемещений. Будем
исходить из того, что вся работа
совершенная внеш. силами переходит в
энергию упругой деф-ции. Искомое
переме-щение
 войдет в ур-ие А=U
лишь в том случае, если в направлении
этого перемещ. В сист. будет приложена
сила, кот. совершает на этом перемещ.
Т.к в общем случае такая сила может и не
быть.Приложим в точку к случайную силу
войдет в ур-ие А=U
лишь в том случае, если в направлении
этого перемещ. В сист. будет приложена
сила, кот. совершает на этом перемещ.
Т.к в общем случае такая сила может и не
быть.Приложим в точку к случайную силу
 =
= ,
если Nk
и EF
-const
то
,
если Nk
и EF
-const
то
 =
= Np-продол.
усилие в стержне от внешней нагрузки.
Np-продол.
усилие в стержне от внешней нагрузки.
 от
единичной случ.силы.
от
единичной случ.силы.
 =
= -взаимное
перемещение сечений,
при этом суммирование проводится в
участке k1,
только здесь Nk1k2
отличается от 0.
-взаимное
перемещение сечений,
при этом суммирование проводится в
участке k1,
только здесь Nk1k2
отличается от 0. =
= .
.
 =
=
 – температ.перемещ.
Слогаемые в этой форму. будет положит.
если характер деф-ции от температурного
поля и от единичной нагрузки одинаково.
– температ.перемещ.
Слогаемые в этой форму. будет положит.
если характер деф-ции от температурного
поля и от единичной нагрузки одинаково.

21-22 Статически опред. и статич. неопред. системы. Каноническое ур-е метода сил. Сист., реакц. внеш. и внутр. связей в котор. можно найти, используя лишь ур-ия статики, наз. статически определимыми. Канонич. метод сил. Для опред. усилий в статич. неопред. конструкциях. Алгоритм: 1. составляем основную систему в каторой искомые усилия заменяем силами Х1, Х2, … Хn. 2. определяем все усилия Nj1¯ под действием только силы Х1, затем Nj2¯ для Х2 и т. д… причем другие Х и внеш. нагрузка Р приравн. к 0. (j – номер стержня). 3. определяем все усилия Njр в стержнях под действием внешней нагрузки Р, без учета "лишних" стержней. 4. определяем коэфф. hk = j=1m(Njh¯Njk¯lj/EFj). kp = j=1m(Njk¯Njplj/EFj). j = 1, 2, …, m – номер стержня. 5. составляем и решаем систему n ур-ий: 11Х1 + 12Х2 + … + 1nХn + 1р = 0; …; n1Х1 + n2Х2 + … + nnХn + nр = 0. Находим Х1, Х2, … Хn. 6. наконец, находим истинные усилия в стержнях по ф-ле: Nj = Nj1¯Х1 + … + Njn¯Хn + Njp. Определение монтажных усилий.Пусть один стержень на короче, чем надо. Приложим в этом стержне стягивающее точки усилие Х1. Уравнение будет иметь вид: 11Х1 = . Отсюда находим Х1 и все остальное.
23. Расчет элементов конструкций, работающих на изгиб. Классификац. видов изгиба. Дифф. зависимости между внутр. силовыми факторами при изгибе. Изгиб – это такой вид деформации, когда в поперечном сечении стержня возникает изгибающий момент. Геометрич. хар-ки поперечн. сечений. Проведем оси коорд. через центр тяж. попереч. сеч. Возьмем малую плошадку dF на сечении. Статич. момент попереч. сеч. отн. оси Х: Sx = FydF (Sy = FxdF). Осевой момент инерции: Ix = Fy2dF (Ix = Fy2dF). Центробежный момент инерции: Ixy = FxydF. (если он = 0, то оси х и у – главные центральные оси). Изогнутая ось стержня наз. упругой кривой. Если все силы лежат в одной з плоскостей инрц., то изгиб наз. прямым. Классификац. изгибов. прямой (чистый Мх = 0, Qy = 0, My 0, Qx = 0; поперечный Qy 0, Qx 0); косой (чистый Qx = Qy = 0; поперечный Mx 0, My 0, Qy 0, Qx 0). Дифф. зависимость: Рис.: балка, посередине на некотор. участке ее рапред. нагр. q. А в нем кусочек dz. Ф-лы: y = 0: Qy + qdz – (Qy + dQy) = 0. dQy/dz = 0. mom = 0: Qydz + Mx + qdz(dz/2) – Mx – dMx = 0. dMx/dz = Qy. d2Mx/dz2 = q.
24. Чистый прямой изгиб. Нормальные напряжения при чистом изгибе. Расчеты на прочность. Рациональные формы попереч. сечений при изгибе. Чистый изгиб балки: Mx = - FdFy (Mу = - FхdF). Вывод ф-лы для кривизны нейтр. слоя при чистом изгибе. Рис.: стержень nn, в нем кусок длиной dz, причем на высоте у от линии nn помечен отрезок АВ. Сечение овальное. После изгиба: прложен момент по краям Mx, радиус кривизны , отрезок АВ перешел в A'B', угол его d. dz = d. = (A'B' – AB)/AB = (( - y)d - d)d = - y/. Итак: = - y/. = E = - Ey/. Нарис. график попереч. напряж. Т. к. изгиб чистай, Мх 0; Nz = 0; My = 0; Qy = 0; Qx = 0… Nz = FSdF = 0. F(- Ey/)dF = 0 FydF = 0. Статич. момент: SN-N = FydF = 0 ось N-N – проходит через центр тяжести сечения. Qx, Qy – главные центральные оси. Mx = - FydF = = F(E/)y2dF = (E/)Fy2dF. Осевой момент инерции Ix = Fy2dF. Mx = EIx/. Кривизна 1/ = Мx/Eyx жесткость сечения при изгибе. Фор-ла для напряж. при чистом изгибе. = - (E/)y = - (Mx/Ix)y. = - (Mx/Ix)y. Момент сопротивления при изгибе. Пусть сечение – симметрично отн. оси ОХ. Рис. оси, сечение – овал. Высота h, отн-но горизонт. оси до краев ymax = h/2. max = (Mx/Ix)ymax. Wx = Ix/ymax. max = Mx/Wx. Рац. попереч. сеч. при изгибе. для пластичн. матер. – симметричн, т. к. []p = []c. (растяж. сжатие). Для хрупких – антисимм., т. к. []p []c (иногда в несколько раз). Расчет на прочность: max = Mx/Wx. dMx/dz = Qy.. Прямой поперечный изгиб. Мх 0, Qy 0. Mx = - FydF. Qy = ∫FdF. (Наруш. гипот. плоских. сеч., наруш. гипот. о не надавл. волокон). Нормальные напряжения: = - (Mx/Ix)y. Касат. напряж: ф-ла Журавского: = QySx/Ixb. Qy – поперечная сила. Ix – осевой момент сечения. b – ширина сечения. Sx - статич. момент отсеченной части. Рис.: оси х и …, овал, вверху примерно на половине линия, отсек. верхн. часть, длина ее b, на ней действуют (направл. ). Рис. 2: тоже, но верхн. часть заштрих., ее плошадь – F, расст. от оси х до ее центра – x(?).Статич. момент попереч. сеч. отн. оси Х: Sx = FydF (Sy = FxdF).
25.
Определение перемещений при изгибе.
Энергетический метод Примем
гипотезы:1)материал следует закону Гука.
2)силы прикладываются квазистатически.3)перемещения
малы. Чистый изгиб: Поперечный изгиб:
Поперечный изгиб:

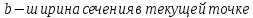 .
.
 Интеграл Максвелла – Мора для деформации
изгиба Перемещения в системе
определяются следующим образом:
Интеграл Максвелла – Мора для деформации
изгиба Перемещения в системе
определяются следующим образом:
растяжение изгиб
Для
вычисления
 необходимо:1)Построить эпюру
необходимо:1)Построить эпюру
 в системе загруженной внешними
силами.2)Построить эпюру
в системе загруженной внешними
силами.2)Построить эпюру
 .
Причём, если требуется найти
.
Причём, если требуется найти
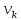 ,
прикладывается
,
прикладывается
 .
Если ищется
.
Если ищется
 ,
то прикладывается
,
то прикладывается
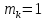 .Интеграл
Максвелла – Мора может вычисл. двумя
способами: по правилу Вере-щагина и по
ф-ле Симпсона .Ф. Симпсона:
.Интеграл
Максвелла – Мора может вычисл. двумя
способами: по правилу Вере-щагина и по
ф-ле Симпсона .Ф. Симпсона:
 Применима, если:1)
Применима, если:1) – длина участка, где эпюры идут по
одинаковым законам.2)
– длина участка, где эпюры идут по
одинаковым законам.2)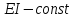 на отрезке
на отрезке
 .3)
.3) .
.
