
Лекция 10
.pdf
Лекция 10
3.2.2 Сходимость градиентных методов.
Во всех рассмотренных выше градиентных методах рекуррентная последовательность xk сходится к стационарной точке f ( x) при достаточно общих предположениях относительно свойств функции. В частности справедлива следующая теорема.
Теорема: Если f ( x) ограничена снизу, ее градиент удовлетворяет условию Липшица (3.1.10), и выбор значения k производится одним из описанных выше способов, то какова бы ни была начальная точка x0 :
f ( xk ) 0.
k
В предположениях теоремы оценить скорость сходимости градиентного спуска не представляется возможным. Это можно сделать, если на f ( x) накладываются более сильные условия. Например, пусть f ( x) – сильно выпуклая функция – это дважды непрерывно дифференцируемая
функция, матрица |
вторых |
производных |
которой при |
x, y En |
|||||||||||
удовлетворяет |
условию |
m |
|
y |
|
2 |
( f |
|
|
y |
|
2 |
, |
где |
|
|
|
|
|
||||||||||||
|
|
|
( x) y, y) M |
|
|
|
|||||||||
M m 0 – некоторые числа.
Теорема: Пусть f ( x) – сильно выпуклая функция, а xk строится по градиентному методу с дроблением шага с выбором шага из условия
(3.2.11) (метод наискорейшего спуска). Тогда xk сходится к точке минимума со скоростью геометрической прогрессии со знаменателем
q |
M m |
, т.е. при достаточно больших k выполнено неравенство |
|||||||||||||||||||
M m |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
x x* |
|
|
|
|
M m |
|
|
|
|
|
x x* |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
M m |
|
|||||||||||
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
k |
|
|
|
|||
|
|
|
|
|
|
|
|
Эффект оврагов. |
|
||||||||||||
|
В качестве M и m в |
|
теореме сходимости градиентных |
методов |
|||||||||||||||||
можно |
|
взять |
максимальное и |
|
минимальное |
собственные числа |
матрицы |
||||||||||||||
|
|
* |
). Если M и m мало отличаются друг от друга (матрица |
|
|||||||||||||||||
f ( x |
|
f ( x) |
|||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||

хорошо обусловлена), то число q мало, следовательно, сходимость методов достаточно высокая. Если же Mm 1, то q близко к 1 и градиентные
методы начинают сходиться плохо. Этот факт хорошо интерпретируется геометрически (рис. 3.2.7) и известен в литературе как эффект оврагов.
Рис. 3.2.7
Поведение градиентного метода при минимизации «овражной» функции: линии уровня f имеют «овражную» структуру и направление
вектора |
|
|
|
|
отклоняться |
от направления в точку |
|||
|
f ( xk ) может сильно |
||||||||
минимума x* . |
|
|
|
|
|
|
|
||
Пример 15. |
|
Вычислить |
градиенты |
функции |
Розенброка |
||||
f ( x , x |
2 |
) 100( x |
2 |
x2 )2 (1 x )2 |
в |
точках |
M |
( 1.2;1), |
|
1 |
|
1 |
1 |
|
|
1 |
|
||
M2 (0;0), M3 (1.5;1) и сравнить полученные направления антиградиента |
|||||||||
с направлениями в точку минимума (1,1) (рис. 3.2.8). |
|
|
|||||||
|
|
|
|
|
2 |
|
|
2 |
|
gradf 400x1 ( x2 x1 ) 2(1 |
x1 );200( x2 x1 ) , |
||||||||
f (M1 ) 215.6;88 2.45;1 ; f (M2 ) 2,0 ;
f (M3 ) 751,250 ( 3,1).
|
|
|
1 |
|
|
M(1,1) |
: M1 M 2.2;0 ; M2 M 1,1 ; M3 M |
|
|
,0 . |
|
2 |
|||||
|
|
|
|
2
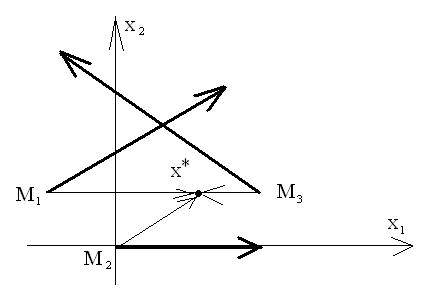
Рис. 3.2.8
Движение к минимуму «овражной» функции в градиентном методе носит явно выраженный зигзагообразный характер – «рыскание» метода, что является его существенным недостатком.
На рисунке 3.2.9 изображена «траектория движения» метода наискорейшего спуска в задаче минимизации функции Розенброка. Гладкие кривые – линии уровня функции, отрезки ломаной соответствуют шагам спуска на отдельных итерациях. Шаги определялись одномерным поиском. Алгоритм начал работать с точки ( 1.2;1)T и мог бы надолго «застрять» в
окрестности точки (0.3;0.1)T , если бы не помогла счастливая случайность
– на одной из итераций процедура одномерного поиска неожиданно нашла второй минимум по направлению. После этого было выполнено еще несколько сот итераций, но ощутимого изменения целевой функции это не дало. Счет был прерван после 1000 итераций вдали от искомого решения. Пример умеренно плохо обусловленной функции подтверждает, что существование доказательства формальной сходимости метода и отсутствие его реальной сходимости (за приемлемое число шагов) вполне совместимы.
3

Рис. 3.2.9
Пример 16. Проанализировать работу градиентного метода для функции f ( x) x12 16x22 .
Рис. 3.2.10
Линии уровня сильно вытянуты вдоль оси x1 (рис. 3.2.10). Матрица
|
|
2 |
0 |
|
|
вторых производных постоянна и равна |
f ( x) H |
|
|
|
, |
|
|
0 |
32 |
|
|
минимальное собственное число равно 2, максимальное собственное число равно 32, т.е. сильно различаются между собой. Траектория градиентного метода характеризуется довольно быстрым спуском на «дно» оврага и затем медленным зигзагообразным движением в точку минимума.
4
Чтобы избежать этого, применяют изменение масштабов независимых
n |
|
переменных. Пусть f ( x) i xi2 , где i |
0 сильно различаются между |
i 1 |
|
собой. Поверхности уровней соответствующим малым i .
того, что в новых переменных
достаточно принять i |
|
1 |
|
|
|
|
|
||
|
|
|
||
i |
|
|||
|
|
|
||
этой функции вытянуты вдоль Заменой переменных xi i yi yi линии уровня стали сферами.
осей xi , добьемся Для этого
, тогда получим преобразование xi |
yi |
|
. |
||
|
|
|
|||
i |
|||||
|
|
|
|||
|
В примере |
16 |
|
движение начато |
из |
точки |
x |
0 |
(2,2)T |
. Т.к. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
составляющие |
градиента |
сильно |
различаются |
|
|
между |
|
|
собой |
|||||||||
|
f |
( x ) 4, |
f |
|
( x ) 64 , |
то, следовательно, получим направление |
||||||||||||
|
x1 |
|
|
|||||||||||||||
|
0 |
|
|
x2 |
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
спуска, существенно отклоняющееся от направления |
в |
точку минимума |
||||||||||||||||
|
x* (0,0). |
Сделаем |
замену |
переменных: |
y x , y |
4x |
2 |
, |
тогда |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
2 |
|
|
|
|
f ( y) y2 |
y2 |
, вектор grad в точке (2,8) действительно направлен в |
|||||||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точку минимума, а линии уровня стали окружностями (рис. 3.2.11).
Рис. 3.2.11
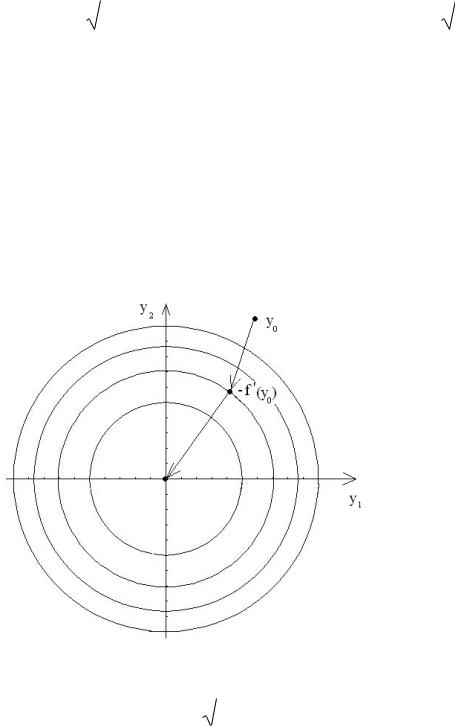
Гарантированное исправление топографии функции – применение
|
|
|
преобразования координат вида y |
|
|
f ( x) x приводит к методу |
||
5 |
|
|

Ньютона, который будет рассмотрен позже (здесь f ( x) – симметричная,
положительно определенная матрица). Если функция f ( x) слишком сложна, чтобы ее продифференцировать аналитически, то вторые производные аппроксимируются их конечно-разностными аналогами.
Масштабирование переменных в общем случае приводит к итерационному процессу вида
где
Bk
Bk
|
|
|
xk 1 |
xk |
|
(3.2.12) |
|
|
|
k Bk f ( xk ), |
|||
матрица |
Bk |
зависит |
от |
номера итерации, |
в примере 16 |
|
1 |
0 |
|
|
|
|
|
B |
1 |
|
. Такие методы называются релаксационными, при |
|||
0 |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
E – обычный градиентный метод.
3.2.3 Эвристические схемы
Рассмотрим две из эвристических схем. Пусть в т. Mk |
вычислены |
||||||||||||
|
f |
|
|
|
|
|
|
|
|
|
|
||
|
|
, i |
1, n |
. |
|
|
|
|
|
|
|
||
|
x |
|
|
|
|
|
|
|
|
||||
|
i |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
а). Зададим малое 1 и положим |
|
f |
|
0, если |
|
f |
|
|
. Тогда |
||||
|
|
|
|
|
|||||||||
|
x |
|
|
x |
i |
||||||||
|
|
|
|
|
|
i |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
f
спуск производится по тем переменным, в направлении которых xi
достаточно велика. Это позволяет быстро спуститься на «дно оврага».
б). Зададим большое M 1 и положим |
f |
|
0, если |
|
f |
|
|
M . |
|
x |
i |
x |
i |
||||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
В этом случае перемещение происходит по «берегу» оврага вдоль его «дна». Комбинация эвристических схем а) и б) дает следующее: в
подпространстве «быстрых переменных» (а).) спуск идет до зацикливания, т.е. до тех пор, пока каждая следующая (k 1) итерация позволяет найти точку, в которой значение f ( xk 1 ) f ( xk ). После этого «включается» процедура б). в подпространстве «медленных» переменных.
6
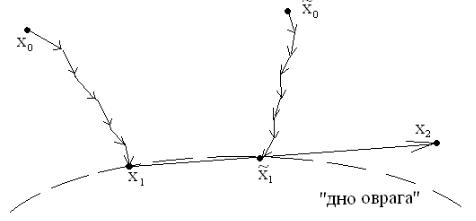
Другие идеи лежат в основе овражного метода, разработанного
Гельфандом И.М. в начале 60-х годов. Пусть и ~ – две любые близкие
x0 x0
точки. Из них производится обычный градиентный спуск и после нескольких
итераций с малым шагом |
~ |
|
попадем в точки x1 и x1 |
, которые лежат в |
окрестности «дна» оврага. Соединяя их прямой, делаем «большой овражный шаг» в полученном направлении, перемещаясь вдоль «оврага». В
результате получим точку . В ее окрестности выбираем точку ~ и
x2 x2
повторяем процедуру (рис. 3.2.12). Схемы называются эвристическими, т.к. их сходимость строго не установлена.
Рис. 3.2.12
3.2.4 Метод покоординатного спуска.
В основе метода лежит стремление уменьшить объем вычислительной работы, требуемой для осуществления одной итерации метода наискорейшего спуска.
Пусть x0 x01 , x02 ,...,x0n T
f ( x0 ) |
x1 x0 0e1 |
f ( x0 ) |
e1 |
|
T |
|
и примем |
, где |
1,0,...,0 |
– |
|||
x1 |
|
x1 |
|
|
|
|
единичный вектор оси x1 . Следующая итерация состоит в вычислении точки
x |
x |
e |
|
f ( x1 ) , где e |
|
0,1,...,0 T – единичный вектор оси x |
|
2 |
1 |
1 |
2 |
x2 |
2 |
|
2 |
|
|
и т.д. Следовательно, спуск идет по ломаной, состоящей из отрезков прямых, параллельных координатным осям (рис. 3.2.13). Спуск по всем n координатам составляет одну «внешнюю» итерацию.
7
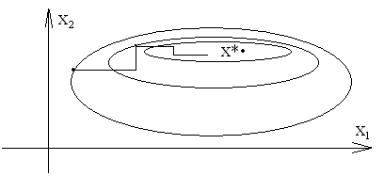
Рис. 3.2.13
Пусть k – номер очередной внешней итерации, а s – номер той координаты, по которой производится спуск, тогда рекуррентная формула для следующего приближения к точке минимума вычисляется по формуле
x |
kn s 1 |
x |
kn s |
|
kn s |
f ( xkn s ) e , |
||||||
|
|
|
xs |
|||||||||
|
|
|
s |
|||||||||
где k 1,2,..., s |
|
или в координатной форме |
||||||||||
1, n |
||||||||||||
xkn s 1 i xkn s i , i s , |
|
|
|
|
|
|
||||||
xkn s 1 i xkn s i |
|
|
|
f ( xkn s ) |
|
|
|
|||||
kn s |
i s , k 1,2,..., s 1, n. |
|||||||||||
xs |
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
После окончания работы внутренней итерации при s n номер внешней итерации увеличивается k k 1. Если k const , то получим
покоординатный спуск с постоянным шагом. Если k выбирается из
|
|
|
|
f |
|
|
условия минимума функции |
( ) |
|
es |
|
, то приходим к |
|
|
f xkn s |
|
|
|
||
|
|
|
|
xs |
|
|
методу Гаусса-Зейделя (координатный аналог метода наискорейшего спуска), частный случай общего релаксационного процесса (3.2.13)
xk 1 xk Bk k k , |
(3.2.13) |
где в матрице Bk все элементы, кроме одного (определяется номером
итерации), стоящего на диагонали, равны нулю.
Заключение: достоинство градиентных методов заключается в простоте реализации и возможности использования для минимизации различных по характеру функций; недостаток – медленная сходимость при плохой
обусловленности f ( x), что соответствует сложной топографической структуре f ( x) («овраги» и «хребты»). Пути преодоления – «исправление»
|
для построения методов, |
поверхности f ( x), использование f ( x) |
|
которые не «реагируют» на овражную структуру |
f ( x). |
8 |
|
