
Лекция 9
.pdfЛекция 9
3.1.5 Метод наискорейшего спуска
Как правило, в градиентном методе с постоянным шагом шаг оказывается очень малым, что приводит к возрастанию итераций для достижения точки минимума. Поэтому, градиентный метод с дроблением шага более экономичен. В отличие от других градиентных методов в методе наискорейшего спуска на каждой итерации шаг выбирается из условия минимума функции в направлении движения. Процесс, на каждой итерации
которого шаг k выбирается из условия
f ( xk k f |
|
|
(3.1.11) |
( xk )) min f ( xk |
f ( xk )) |
||
|
0 |
|
|
называется методом наискорейшего спуска. На каждой итерации требуется решать задачу одномерной минимизации. Этот способ выбора k сложнее, чем в первых двух методах.
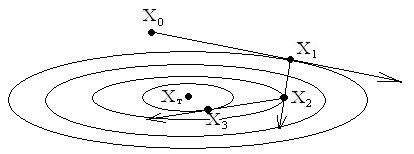
Этот метод в литературе известен еще как метод Гаусса-Зейделя. Геометрическая интерпретация: В отличие от первых двух методов
направление движения из точки xk касается линии уровня в точке xk 1 .
Ломаная x0 x1 ...xk зигзагообразно приближается к x* , причем звенья этого зигзага ортогональны между собой. В самом деле, шаг выбирается из
условия |
|
|
|
|
|
поэтому |
||
|
|
min ( ) min f ( xk f ( xk )), |
||||||
|
|
|
|
|
|
|
|
|
|
d ( k ) |
|
f |
|
( xk 1 ) f |
|
( xk ) 0, следовательно, направления спуска |
|
|
d |
|||||||
|
|
|
||||||
|
|
|
|
|
|
|
||
на двух последовательных итерациях взаимно ортогональны (рис.3.1.5).
1

С1 С2 С3 ....
Рис.3.1.5
Достоинство: обеспечивает движение с самым выгодным шагом. Недостаток: на каждой итерации предполагается решение довольно
трудоемкой вспомогательной задачи одномерной минимизации. Алгоритм метода наискорейшего спуска:
10 . Выбрать любое x0 Rn , положить k 0.
Основной цикл: 20 . Вычислить f ( xk ).
30 . Если f ( xk ) 0, то x* xk и выход из алгоритма, иначе перейти к шагу 40 .
40 . Вычислить k из условия
f( xk f ( xk )) min f ( xk f ( xk )).
0
50 . Вычислить xk 1 xk k f ( xk ).
60 . Положить k k 1 и перейти к шагу 20 .
На практике окончание работы алгоритма происходит при выполнении
условия |
|
f |
xk |
|
, i 1,2, ,n , где |
– заданная точность. |
|
|
|
|
|||||
|
|
|
|
|
|||
xk |
|
||||||
|
|
|
|
|
|
||
|
|
Рассмотрим работу метода наискорейшего спуска на примере |
|||||
нахождения |
|
|
минимума |
квадратичной |
функции |
||
z ax2 bxy cy2 dx ey f . Так |
как эту функцию с |
помощью |
|||||
|
|
|
|
2 |
|
|
|
линейных преобразований (перенос начала системы координат и поворот
осей) можно привести к каноническому виду |
z a x2 |
b y2 |
, то |
||
|
1 |
1 |
1 |
1 |
|
ограничимся рассмотрением алгоритма нахождения минимума приведенной к каноническому виду квадратичной функции.
|
Пример 14. Найти минимум функции z ax2 by2 |
с точностью до , |
|||||||||||||||||||
если начальное приближение X0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
2ax0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1. Вычислим градиент функции gradz |
|
|
|
|
|
|
. |
|
||||||||||||
|
|
|
zx , zy |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X0 |
|
|
|
|
2by0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2. Составим |
уравнение |
прямой с |
|
направлением |
|
gradz |
и |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X0 |
проходящей |
через |
точку |
|
X : |
|
x x0 |
|
y y0 |
|
. |
Отсюда |
||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zx |
|
|
|
zy |
|
|
|
|
|
by |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
0 |
x y0 |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ax0 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. Среди всех линий уровня ищем ту, для которой найденная прямая является в то же время касательной к этой линии уровня. Обозначим точку
касания X1 |
x |
|
|
|
1 |
(рис.3.1.6). |
|
|
|
y1 |
|
|
Рис. 3.1.6 |
|
|
|
|
|
|
|
|
|
|
|
3. |
Запишем уравнение линии |
|
уровня |
поверхности |
z C : |
|||||||
ax2 by2 |
C или в каноническом виде |
x2 |
|
y2 |
1 |
, где a2 |
|
C |
, b2 |
|
C |
|
a2 |
b2 |
|
|
|
||||||||
|
|
|
|
1 |
|
a |
1 |
|
b |
|||
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
. Кривая, описываемая этим уравнением – эллипс.
3
4. Запишем уравнение касательной к эллипсу в точке касания X1 :
|
xx |
|
yy |
1. Отсюда находим |
y |
b2 |
|
x |
x |
b2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
1 |
1 |
|
1 |
|
1 |
. |
|
Из |
условия |
||||||||||||||
|
a2 |
b2 |
a2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
y |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
1 |
|
|
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
|
|
2 |
|
x1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
b1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
y1 |
||||||||||
совпадения этой касательной с направлением градиента |
a x0 |
|
|
|
a1 |
|
|||||||||||||||||||
|
|
|
b |
|
b12 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y0 |
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||||||||||
получим координаты точки X1 , зависящие от C : x1 |
|
|
bC |
, |
|
|
|
||||
ax0 |
a b |
||||
|
|
|
y1 |
|
|
aC |
. |
|
|
|
||||
by0 |
a b |
||||
|
|
|
5. Так как точка координат x1 , y1
abx2 y2 a b 2
C 0 0 . a3 x02 b3 y02
x1 |
b2 y2 x |
0 |
a b |
|
0 |
|
, |
||
a3 x2 |
b3 y2 |
|||
|
0 |
|
0 |
|
X1 |
принадлежит и |
эллипсу, то при подстановке |
||||||
в |
уравнение |
эллипса |
получим |
значение |
||||
Таким |
образом, |
координаты точки |
X1 : |
|||||
y1 |
a2 x2 y a b |
|
|
|
|
|||
0 |
0 |
|
. |
|
|
|
|
|
a3 x2 |
b3 y2 |
|
|
|
|
|||
|
0 |
|
0 |
|
|
|
|
|
Теперь из точки X1
действия для нахождения каждого приближения к
проводим градиент и повторяем вышеописанные следующей точки X2 (рис.). После нахождения точке минимума функции проверяем условие
|
X |
k 1 |
X |
k |
|
|
x |
k 1 |
x |
k |
2 |
y |
k 1 |
y |
k |
2 |
. При достижении заданной |
||
|
|
||||||||||||||||||
точности за точку минимума функции принимаем X X |
n |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
