
Лекция 7
.pdfТема 3.1.
Градиентные методы
Численное решение задач безусловной минимизации функций многих переменных, как правило, значительно сложнее, чем решение задач минимизации функций одного переменного. В самом деле, с ростом числа переменных возрастают объемы вычислений и усложняются конструкции вычислительных алгоритмов, а также более сложным становится анализ поведения целевой фунции.
Методы численного решения задач многомерной безусловной минимизации многочисленны и разнообразны. Условно их можно разделить на три больших класса в зависимости от информации, используемой при реализации метода.
1.Методы нулевого порядка, или прямого поиска, стратегия которых основана на использовании информации только о свойствах целевой функции.
2.Методы первого порядка, в которых при построении итерационной процедуры наряду с информацией о целевой функции используется информация о значениях первых производных этой функции.
3.Методы второго порядка, в которых наряду с информацией о значениях целевой функции и ее производных первого порядка используется информация о вторых производных функции.
Методы первого и второго порядков хорошо разработаны. Для большинства из них имеется строгое обоснование, проведено аналитическое исследование их свойств, доказана сходимость, получены оценки скорости сходимости для некоторых классов целевых функций.
3.1.1Условия оптимальности функции многих переменных
Пусть f ( x) – скалярная функция векторного аргумента размерности
n, т.е. |
X E |
n |
. Если |
x* ( x* , x* ,...,x* )T |
– точка ее безусловного |
||||||||||
|
|
|
|
|
|
|
1 |
2 |
|
n |
|
|
|
|
|
локального |
экстремума, |
то |
в |
x* |
будет |
достигаться |
экстремум функции |
||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
одной |
переменной |
x |
k |
: f ( x* ,...,x* |
, x |
k |
, x* |
,...,x* ), |
которая |
||||||
|
|
|
|
|
|
|
|
1 |
k 1 |
|
k 1 |
n |
|
||
получается |
из |
|
f ( x), |
если |
зафиксировать |
|
все |
переменные, |
кроме |
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
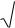
xk : xi xi* для i k . А для функции одной переменной необходимое условие экстремума уже получено.
Теорема: (необходимое условие экстремума I порядка)
Для того чтобы в точке x* функция f ( x1 , x2 ,...,xn ) имела безусловный локальный экстремум, необходимо, чтобы все ее частные производные обращались в точке x* в нуль:
|
f |
|
gradf ( x* ) |
f ( x* ) f ( x* ) 0 . |
|
|
|
|
|||
|
xk |
||||
|
|
x x* |
|
|
|
|
|
|
|
||
Это условие стационарности, которое является системой n уравнений |
|||||
для n уравнений. |
|
|
|||
После того, как решение x* |
системы уравнений |
будет найдено, |
|||
необходимо определить характер стационарной точки x* . |
Для этого нужно |
||||
исследовать поведение f ( x) в окрестности точки x* . Для этого разложим
f ( x) в ряд Тейлора в окрестности |
|
точки x* , |
полагая |
ее |
дважды |
||||||||||||||
непрерывно дифференцируемой по всем переменным x1 ,...,xn . |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
* |
o |
|
|
|
2 , |
|
|||
f ( x* ) f ( x* ) |
1 |
|
n |
|
|
f ( x ) k m |
|
|
|
|
|||||||||
|
|
|
|
|
|
(3.1.1) |
|||||||||||||
|
|
|
|
|
|
||||||||||||||
2 |
k ,m 1 |
xk xm |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где вектор ( 1 , 2 ,..., n )T , |
|
|
|
|
|
|
|
, – |
норма |
вектора , |
|||||||||
|
|
|
|
||||||||||||||||
2 f ( x* ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
– элементы матрицы Гессе |
|
( матрицы |
вторых |
производных |
|||||||||||||||
xk xm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f ( x) ) в стационарной точке x* :
2
|
2 |
f ( x* ) |
|
|
x12 |
|
|
|
f ( x* ) |
|
... |
|
2 |
f ( x* ) |
|
|
|
|
xn x1 |
|
|
||
,.., |
|
2 |
f ( x |
* |
) |
|
|
|
|
|
|
||||
|
x1 xn |
|
|
|
|||
... |
|
|
... |
|
|
|
(3.1.2) |
|
2 |
f ( x* ) |
|
|
|||
,..., |
|
|
2 |
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
Для непрерывной f по теореме Шварца все смешанные производные функции второго порядка равны, поэтому матрица Гессе является симметричной.
Характер стационарной точки x* функции f ( x) связан со знакоопределенностью квадратичной формы
n |
2 f ( x* ) |
|
|
|
|
, f |
|
x |
* |
. |
|
|
|
|
xk xm |
k m |
|
|
|
|
|||||||
k ,m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Напомним, что квадратичная форма называется неотрицательно |
|||||||||||||
определенной в точке x* , если 0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
* |
) |
|
0 |
|
|
|
|
|
(3.1.3) |
|
|
, f |
( x |
|
|
|
|
|
|
|
||||
и положительно определенной, если 0 |
|
|
|
|
|
|
|
||||||
|
|
|
* |
) |
|
0 |
|
|
|
|
|
(3.1.4). |
|
|
, f |
( x |
|
|
|
|
|
|
|
||||
Соответственно, |
симметричная |
|
матрица |
|
|
|
* |
) называется |
|||||
|
|
f ( x |
|
||||||||||
неотрицательно определенной в точке x* , если выполнено условие (3.1.3), и положительно определенной, если выполнено условие (3.1.4).
Теорема: (необходимые и достаточные условия минимума II порядка)
Для того чтобы дважды непрерывно дифференцируемая функция n
переменных f ( x) имела в стационарной точке x* безусловный локальный минимум, необходимо, чтобы матрица ее вторых производных была неотрицательно определенной и достаточно, чтобы она была положительно определенной.
3
Проверка знакоопределенности матриц может быть осуществлена, например, с помощью критерия Сильвестра. Согласно этому критерию, необходимым и достаточным условием положительной определенности
квадратичной |
|
формы |
|
|
|
x, Ax , |
где |
|
|
|
|
|
– |
симметричная n n |
|||||||||||||||||||||||||||||
матрица, является выполнение n неравенств: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
a11 |
a12 |
|
0, |
|
|
|
|
|
a11 ... |
a1n |
|
0. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
..., |
... ... |
... |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an1 ... ann |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Пример |
|
|
8. |
|
|
|
|
|
Определить |
экстремальные |
значения |
функции |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
f ( x) |
|
|
1 |
|
|
|
2 |
|
,a,b 0, X E |
|
. |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Выполнение |
|
|
|
|
|
|
|
|
|
|
|
|
необходимых |
|
|
|
условий |
|||||||||||||||||||||||
|
f |
|
|
2x1 |
|
0, |
|
|
|
f |
|
|
|
|
2x2 |
0 дает |
координаты |
стационарной точки |
|||||||||||||||||||||||||
|
x |
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x* (0,0)T . |
|
|
|
|
|
|
|
|
Частные |
производные |
второго |
порядка |
||||||||||||||||||||||||||||||
|
2 f |
|
|
2 |
, |
|
|
|
|
|
2 f |
|
|
0, |
2 f |
|
2 |
, |
определяют |
элементы |
матрицы |
||||||||||||||||||||||
|
x2 |
|
a |
|
|
|
x x |
2 |
|
x2 |
b |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Гессе f |
|
|
a |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Согласно последней теореме: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
1) |
|
при |
a 0,b 0 |
f ( x) имеет |
в точке x* (0,0)T |
минимум |
||||||||||||||||||||||||||||||||||
(эллиптический параболоид); |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2)при a 0,b 0 (стационарная точка типа «седло») экстремума нет, гиперболический параболоид;
3)при a 0,b 0 экстремума нет, гиперболический параболоид;
4
4) при параболоид).
a 0,b 0 f ( x) имеет максимум (эллиптический
3.1.2. Обзор численных методов отыскания безусловного экстремума
Численные методы отыскания безусловного экстремума – это прямой метод решения задач оптимизации, который состоит в пошаговом
определении точек x1 , x2 ,..., в которых значения целевой функции образуют убывающую сходящуюся последовательность. Тогда можно найти минимум функции, не прибегая к необходимым условиям. Следовательно, требуется построить некоторую релаксационную последовательностьxk nk 0 , удовлетворяющую условию f ( x0 ) f ( x1 ) ... f ( xn ).
Методы построения таких последовательностей называются методами спуска. Различные методы спуска отличаются друг от друга способами выбора направления спуска и длины шага вдоль этого направления. Во всех
этих методах точки xk находятся по формуле
xk 1 xk k pk , |
(3.1.5) |
где k – длина шага, pk – направление спуска.
Одной из важнейших характеристик методов является скорость сходимости (линейная, сверхлинейная).
Алгоритмы безусловной минимизации делятся на классы в зависимости от максимального порядка производных минимизируемой функции, вычисление которых предполагается.
Методы нулевого порядка (используют значения только самой целевой функции) – методы поиска. Эти методы используются как сами по себе, так и в качестве важного элемента в методах более высокого порядка для поиска минимума функции одной переменной. К этим методам относятся методы пассивного и последовательного поиска, методы Фибоначчи и «золотого сечения».
Методы первого порядка, в которых требуется вычисление первых производных минимизируемых функций, называются градиентными
методами. Известно, что gradf ( x) в точке xk направлен в сторону
5
наискорейшего возрастания функции и ортогонален линии уровня, значит антиградиент функции f ( x) в точке xk , gradf ( xk ), направлен в сторону наискорейшего убывания функции f ( x). Выбирая в (3.1.) в
качестве pk антиградиент, приходим к итерационному процессу вида
|
0 . |
(3.1.6) |
xk 1 xk k f ( xk ) , где k |
Градиентные методы делятся по выбору k : метод дробления шага, метод наискорейшего спуска и т.д.
Градиентные методы достаточно просты в реализации, но плохо работают (медленно сходятся), если матрица Гессе (матрица вторых производных минимизируемой функции) f ( x) плохо обусловлена. Это соответствует сложной топографической структуре функции f ( x) – наличие «оврагов» и «хребтов». Возникает «эффект оврагов». Возможные пути преодоления этого – способы «исправления» поверхности f ( x), например, изменение масштабов независимых переменных целевой функции, некоторые эвристические схемы, которые идейно близки к релаксационным методам, метод покоординатного спуска.
Другой путь – использование вторых производных минимизируемой функции f ( x) для построения методов, которые не «реагируют» на овражную структуру функции f ( x).
Это методы второго порядка, которые требуют наименьшего числа шагов (итераций), но содержат громоздкие вычисления f ( x) для сложной функции.
Методы второго порядка – прямое обобщение известного метода Ньютона отыскания корня уравнения ( x) 0 ( – скалярная функция скалярного аргумента). Метод Ньютона отыскания корня уравнения строится на разложении функции в ряд Тейлора в окрестности некоторой точки xk . Отбрасывая малые высшего порядка, получим линейное уравнение
относительно неизвестной величины x : x x ( xk ) . Рекуррентная
k k ( xk )
формула метода Ньютона отыскания корня уравнения
6
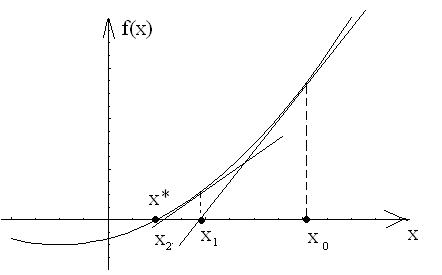
xk 1 xk |
( xk ) |
. |
(3.1.7) |
|
( xk ) |
||||
|
|
|
Такой поиск корня уравнения также называют методом касательных. Геометрическая иллюстрация этого метода приведена на рис. 3.1.1.
Рис. 3.1.1.
Этот метод распространяется на ( x) – n- мерную вектор-функцию векторного аргумента x той же размерности, а затем на вектор-функцию( x) f ( x) – градиент некоторой скалярной величины f ( x).
Таким образом, метод Ньютона (как метод второго порядка) интерпретируется как последовательный поиск точек минимума квадратичных аппроксимирующих функций.
Геометрическая иллюстрация метода Ньютона приведена на рис. 3.1.2
7
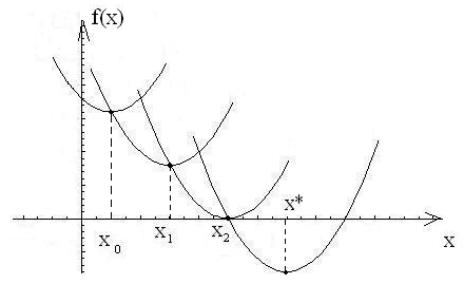
Рис. 3.1.2.
Этот метод более эффективен по сравнению с градиентными методами, т.к. квадратичная функция локально точнее аппроксимирует минимизируемую функцию, чем линейная. Сходимость методов Ньютона
зависит от удачного выбора начального приближения x0 , это не тривиальная задача, следовательно, разрабатываются модификации метода, например, метод Ньютона-Рафсона (независимость от x0 ).
Трудности применения метода Ньютона:
1)вычисление матрицы f ( x),
2)нарушение в процессе счета положительной определенности этой матрицы.
Поэтому существуют различные модификации метода Ньютона.
К методам первого порядка, но с более высокой скоростью сходимости, относят метод сопряженных направлений, частным случаем которого является метод сопряженных градиентов, метод двойственных направлений, основная идея которого состоит в построении процесса спуска, обладающего сверхлинейной скоростью сходимости и не требующего при
этом вычисления f ( x).
Кроме этого, существуют еще методы псевдообратных операторов, метод минимизации вдоль собственных векторов матрицы, близкой к матрице Гессе, итеративные стохастические методы, использующие аналог функции Ляпунова, стохастические квазиградиентные методы, метод локальных вариаций.
8
