Сила давления жидкости на плоскую стенку

Используем основное уравнение гидростатики (1.20) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом а (рис. 1.7). Вычислим силу F давления, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.

Ось направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось — перпендикулярно к этой линии в плоскости стенки.

Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке :

где — давление на свободной поверхности; — глубина расположения пло­щадки .

Для определения полной силы проинтегрируем полученное выражение по всей площади :

где — координата площадки .

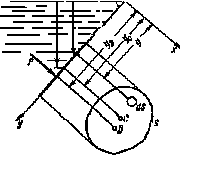
Рис. 1.7

Последний интеграл представляет собой статический момент площади относительно оси и равен произведению этой площади на координату ее центра тяжести (точка С), т. е.

Следовательно,

(здесь — глубина расположения центра тяжести площади S. ),

или

(1.29)

т. е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление в центре тяжести этой площади.

В частном случае, когда давление Р_о является атмосферным и действует также с другой стороны стенки, сила избыточного давления жидкости на плоскую стенку равна лишь силе давления от веса жидкости, т. е.

F_изб=F

В общем случае давление может существенно отличаться от атмосферного, поэтому полную силу давления жидкости на стенку будем рассматривать как сумму двух сил: от внешнего давления и силы от веса жидкости, т.е.

Рассмотрим вопрос о точках приложения этих сил, называемых центрами давления.

Так как внешнее давление передается всем точкам площади одинаково, то его равнодействующая будет приложена в центре тяжести площади . Для нахождения точки приложения силы давления от веса жидкости (точка D) применим теорему механики, согласно которой момент равнодействующей силы относительно оси равен сумме моментов составляющих сил, т. е.

где — координата точки приложения силы . Выражая и через и и определяя , получаем

где J_x— момент инерции площади относительно оси .

Учитывая, что

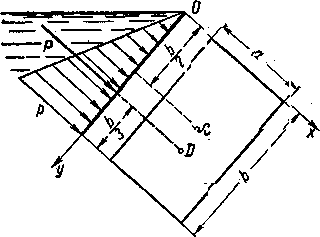
Рис. 1.8 Эпюра давления- жидкости на прямоугольную стенку

(J_x0 — момент инерции площади относительно центральной оси, параллельной ), находим

(1.30)

Таким образом, точка приложения силы расположена ниже центра тяжести площади стенки; расстояние между ними

Если давление равно атмосферному, то точка D и будет центром давления. При выше атмосферного центр давления находят по правилам механики как точку приложения равнодействующей двух сил: F₀ и ; чем больше первая сила по сравнению со второй, тем, очевидно, центр давления ближе к центру тяжести площади S.

В частном случае, когда стенка имеет форму прямоугольника размерами, а х b (рис. 1.14) и одна из его сторон, а лежит на свободной поверхности с атмосферным давлением, центр давления D находится на расстоянии b/3 от нижней стороны.