Лабораторная работа 4

Рассмотрим сложный опыт (X, Y), исходы которого обозначим через (x_i, _j). Энтропия вводится аналогичным образом

. (9)

Если составляющие X, Y сложного опыта независимы, то энтропия сложного опыта равна сумме энтропий составляющих

. (10)

В общем случае вводится понятие – условная энтропия H(Y |X)

, (11)

и формула (8) приобретает следующий вид

.

Для дискретного источника сообщений с алфавитом, состоящим из зависимых попарно символов, энтропия источника определяется в соответствии с формулой (11)

(12)

и характеризует среднее количество передаваемой информации на символ сообщения.

Пример 3. Учтем зависимость между символами в примере 2, заданную матрицей условных вероятностей: .

Рассчитаем энтропию источника по формуле (12)

Подставим числовые данные, используя пример 2,

Таким образом, среднее количество информации на символ сообщения равно 0,64 бит, что меньше 0,88 бит, полученных в примере 2. Это вызвано учетом известной зависимости между символами, что естественно уменьшает неопределенность опыта.

Задачи (блок D)для выполнения:

1 – 10. В условии предыдущей задачи учесть зависимость между символами, которая задана матрицей условных вероятностей P(S_j / S_i).

1. 2. 3.

4. 5. 6.

7. 8. 9.

10.

Лабораторная работа 5

Логические основы построения ПК.

Основы алгебры логики.

Для анализа и синтеза схем в ПК при алгоритмизации решения задач широко используется математический аппарат алгебры логики.

Алгебра логики – это результат математической логики, значения всех (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями.

Высказывание – это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключительного третьего, т.е. каждое высказывание или истинно, или ложно и не может быть одновременно и истинным, и ложным.

Пример: Высказывание: «Сейчас идет снег» - это утверждение может быть истинным или ложным; «Вашингтон – столица США» - исинное утверждение; «Частное от деления 10 на 2 равно3» - ложное утверждение.

В алгебре логике все высказывания обозначают буквами а,b, cи т. д. Содержание высказываний учитывается только при введении их буквенных обозначений, и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй. Причем если над исходными элементами алгебры выполнены некоторые разрешенные в алгебре логики операций, то результаты операций также будут элементами этой алгебры.

Простейшими операциями в алгебре логики являются операции логического сложения (операция ИЛИ, операция дизъюнкции) и логического умножения (операция И, операция конъюнкции). Для обозначения операции логического сложения используют символ + или V, а логического умножения – символы * или ).

Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем и следствий.

В частности, для алгебры логики выполняются законы:

1. сочетательный:

(а + b)+с=а+(b+с);

(a*b)*с=а*(b*с);

2. переместительный:

а + b = b+ а;

а * b = b* а;

3. распределительный:

а*(b + с) = а*b + а*с;

Справедливы соотношения:

а + а = а; a + b = b, если а ≤b;

а* а = а; а* b = а, если а ≤b;

а + а* b = а; a + b = b, если а ≥b

а + b = а, еслиа≥b; и др.

Наименьшим элементом алгебры логики является 0, наибольшим элементом - 1. В алгебре логики также вводится еще одна операция - операцияотрицания(иначе, операция НЕ, операция инверсии),обозначаемая чертой над элементом.

По определению:

Справедливы, например, такие соотношения:

Логический синтез вычислительных схем

Логические блоки, в соответствии с международным стандартом:

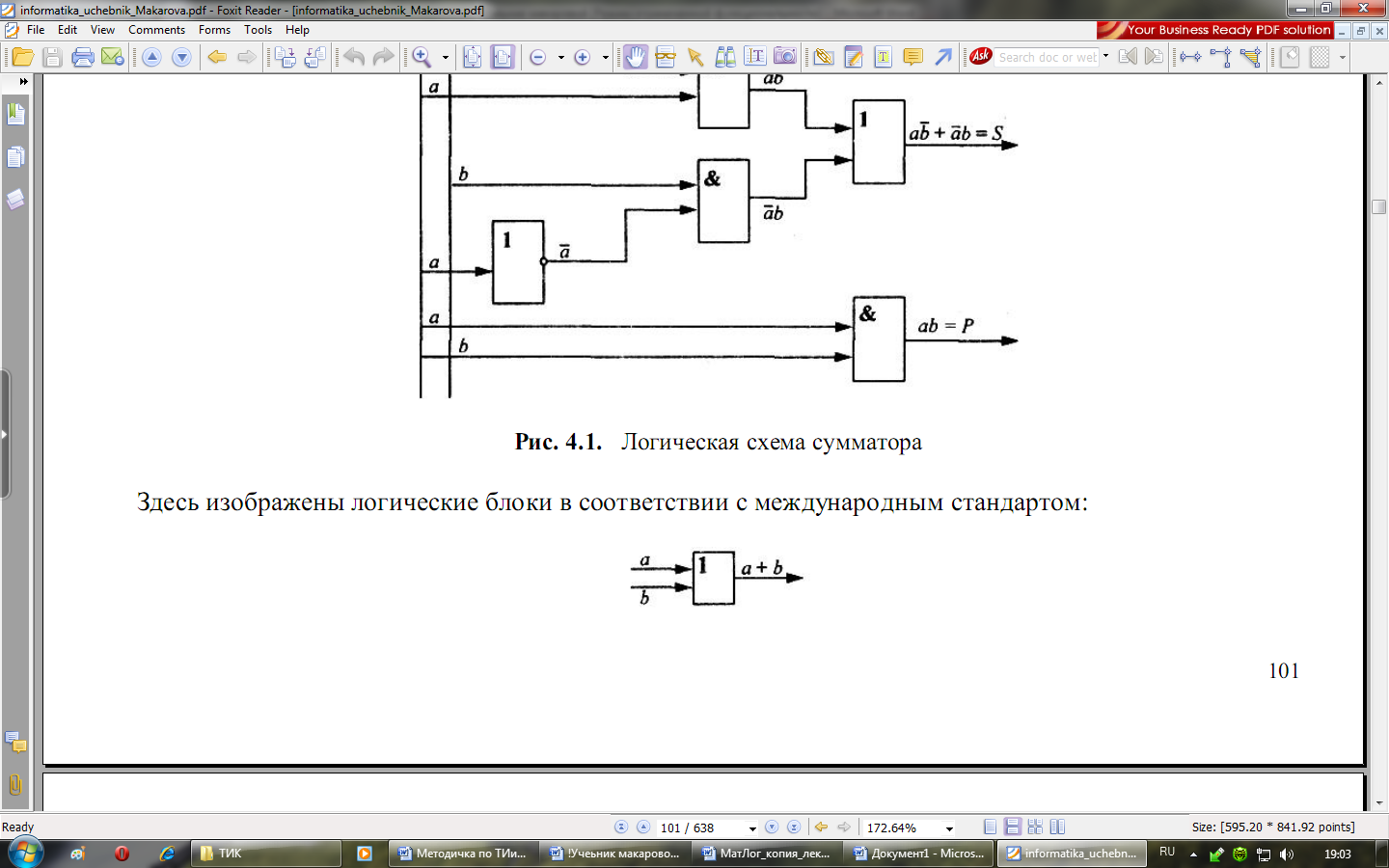
схема ИЛИ, реализующая операцию логического сложения;

схема И, реализующая операцию логического умножения;

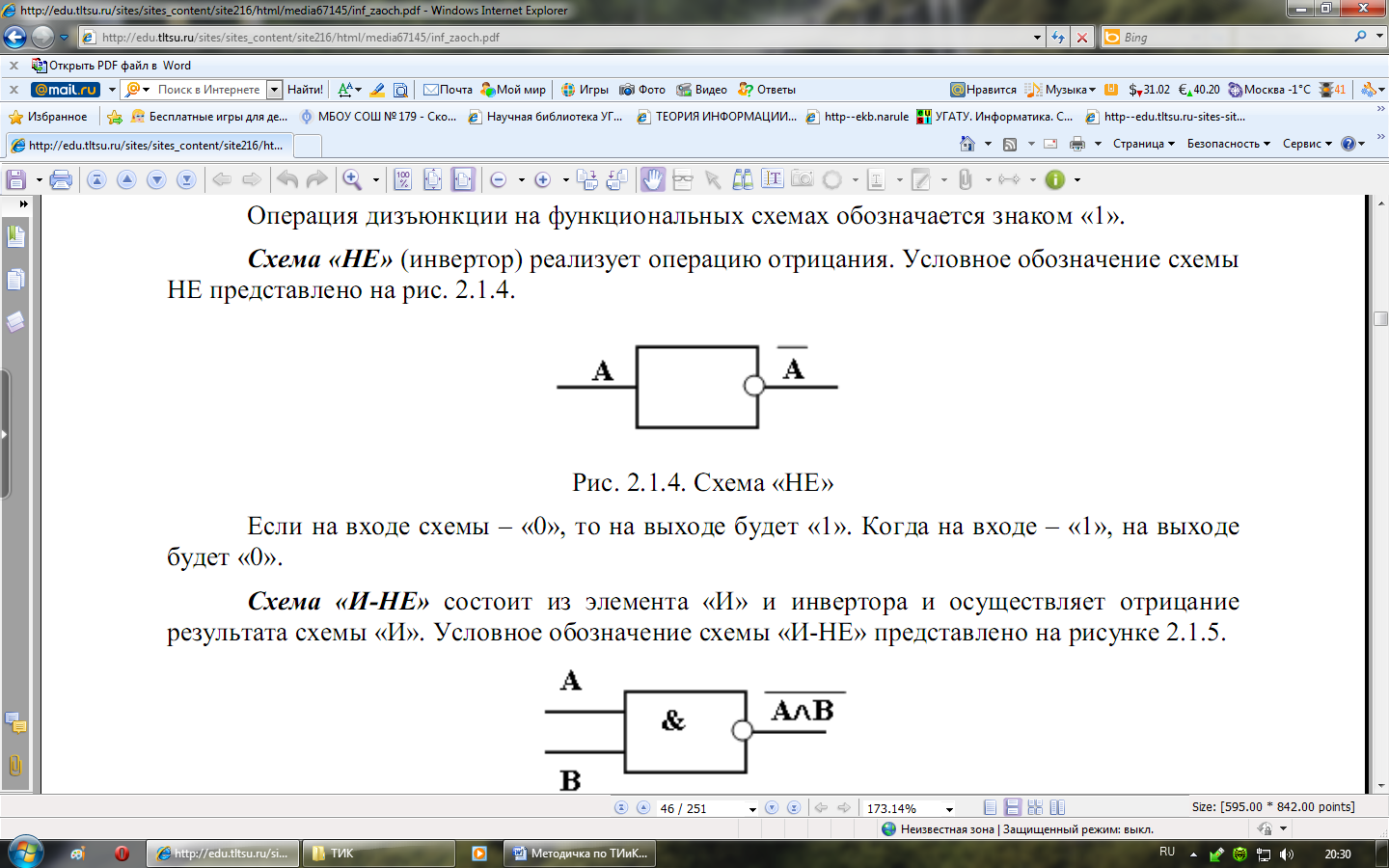
схема НЕ, реализующая операцию инверсии ;

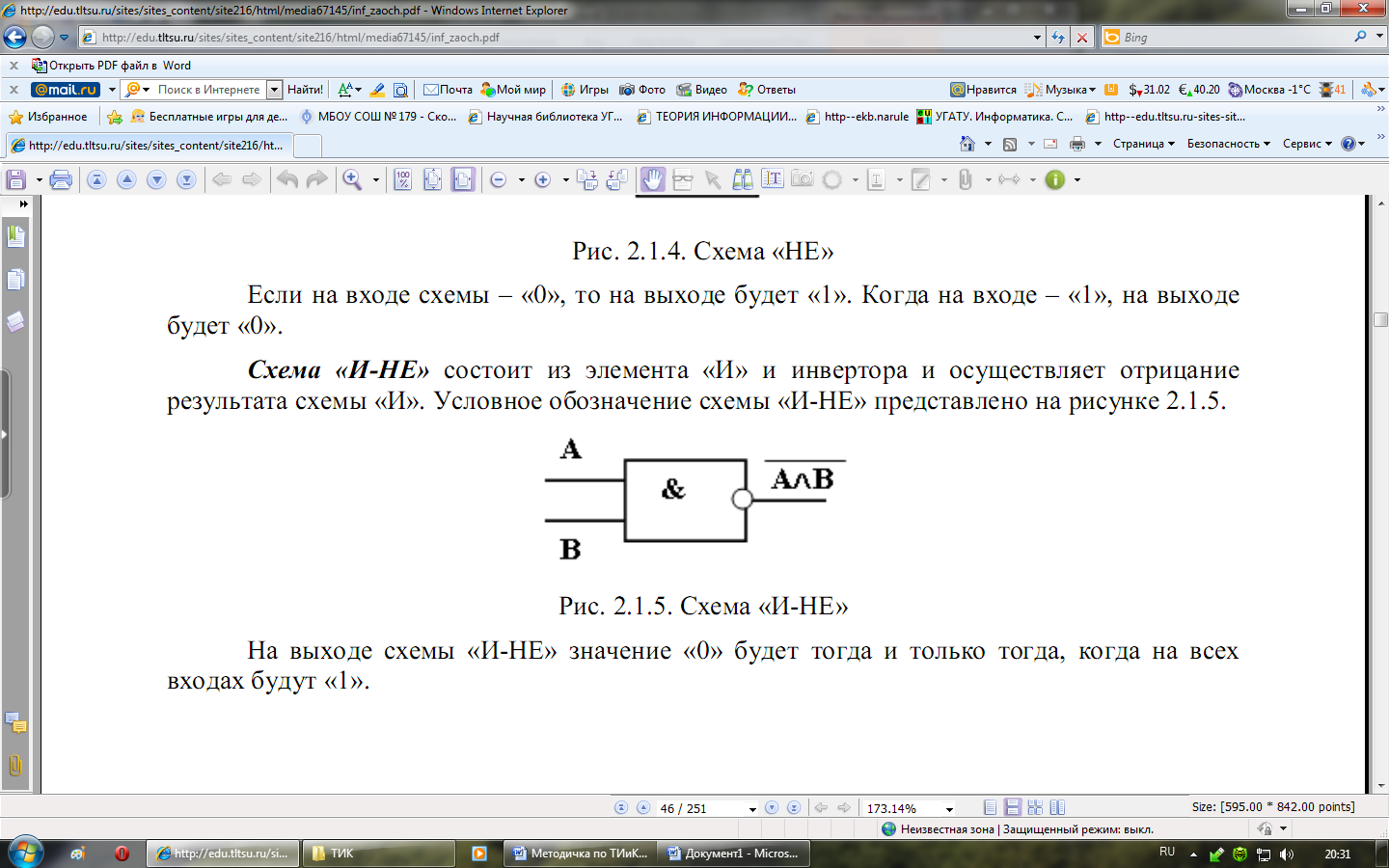
Схема И-НЕ, реализующая операцию инвертора и отрицание результата схемы И.