Лабораторная работа 2

Одно из направлений в измерении информации дает структурная теория, в которой количество информации определяется подсчетом информационных элементов или комбинаций из них.

Рассмотрим аддитивную меру (меру Хартли). Из комбинаторики известно, что число сочетаний с повторениями из h элементов по l равно

.

Таким образом, число всех двоичных кодовых комбинаций длины l равно 2^l (h = 2). В качестве меры информации Хартли предложил взять

(бит). (3)

Тогда 1 бит – это количество информации, содержащееся в двоичной кодовой комбинации единичной длины. Количество информации по Хартли эквивалентно количеству двоичных знаков «0» и «1» при кодировании сообщений по двоичной системе счисления.

Пример 1. Рассмотрим систему, информационная емкость которой определяется десятичным числом Q = 121. Определим количество информации, содержащееся в системе, используя меру Хартли (3),

(бит).

Заметим, что округление результата до целого необходимо проводить в сторону увеличения. Полученный результат означает, что при кодировании числа достаточно использовать 7 двоичных знаков (число возможных двоичных кодовых комбинаций равно 2⁷ = 128)

.

Замечание. Разложение по двоичной системе производится для числа на 1 меньше в силу того, что отсчет ведется от нуля, а число комбинаций равно 121.

Для получения двоичного числа можно использовать метод последовательного деления числа на 2. При каждом делении определяется один двоичный знак кодовой комбинации: если деление без остатка – «0», в противном случае – «1». Ниже приведена таблица, иллюстрирующая метод, столбец справа показывает двоичные знаки кодовой комбинации.

120	2								«0»
	60	2							«0»
		30	2						«0
			15	2					«1»
				7	2				«1»
					3	2			«1»
						1	2		«1»
							0

Двоичное число выписывается в обратном порядке, двигаясь снизу вверх.

При переводе из любой системы счисления в десятичную, нужно целую и дробную части (если есть дробная) умножать по правилам перевода! При переводе числа из десятичной системы в другую, нужно целую часть делить, а дробную умножать по правилам перевода из одной системы счисления в другую!

Примеры перевода чисел из одной системы счисления в другую:

Перевести число 12201₃ из троичной системы счисления в десятичную.

Решение:

^{4 3 21 0 разряды}

12201 ₃=1*3⁴ + 2*3³ + 2*3² + 0*3¹ + 1*3⁰ = 81+54+18+1 = 154₁₀

Ответ: 12201₃ = 154₁₀

Перевести число 234,6₈ из восьмеричной системы в десятичную:

Решение:

^{2 1 0 -1}

234,6₈ = 2*8² +3*8¹ + 4*8⁰ +6*8^-1= 2*64+3*8+4+6*0,125=

=128+24+4+0,75 =156,75₁₀

Ответ: 234,6₈ = 156,75₁₀.

Перевести число 101,01₂ из двоичной системы счисления в десятичную.

Решение:

^{2 1 0 -1 -2 разряды}

101,01₂ = 1*2² + 0*2¹ + 1*2⁰+0*2^-1+1*2^-2 =4+0+1+0+0,25=5,25₁₀

Ответ: 101,01₂ = 5,25₁₀

Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность результата деления и остатков от деления в обратной порядке.

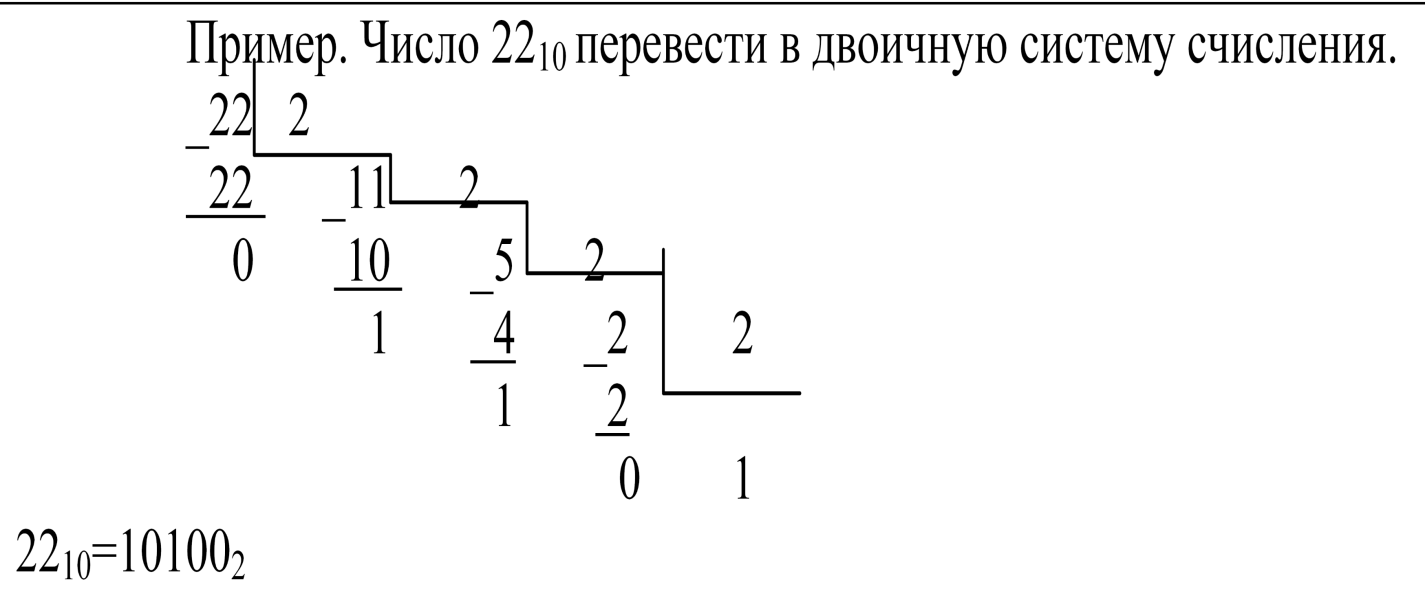
Перевод дробного числа десятичного 0,625₁₀ в дробное двоичное число

Решение: 0,625*2=1,25

0,25*2=0,5

0,5*2=1,0

Ответ: 0,625₁₀=0,101₂

Перевести число 0,165 в четверичную систему счисления, ограничившись четырьмя четверичными разрядами.

Решение: 0,165*4=0,66

0,66*4=2,64

0,64*4=2,56

0,56*4=2,24

Ответ: 0,165₁₀=0,0222₄

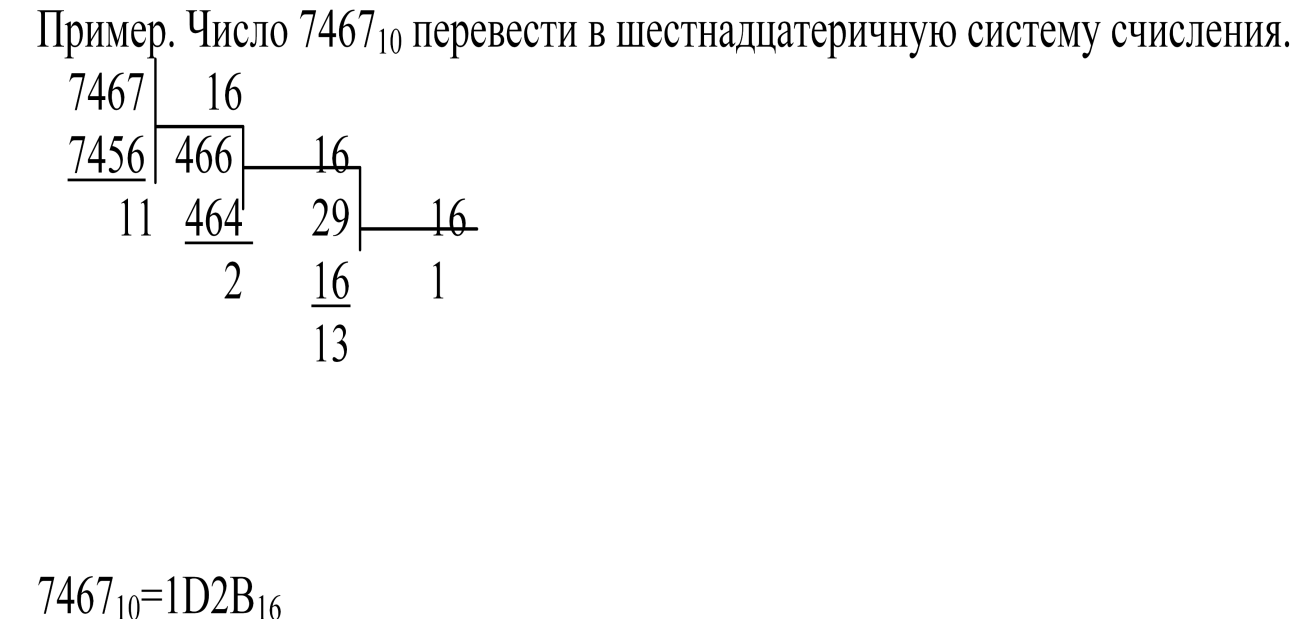
Задание для всех вариантов:

Позиционные системы счисления

1. З 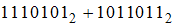начение суммы чисел в восьмеричной системе счисления равно …

2. Двоичному числу 1011101₂ соответствует какое шестнадцатеричное число.

3. Переведите 102,21₃ в десятеричную систему счисления.

4. Переведите 213,21₄ в семеричную систему счисления.

5. С помощью калькулятора программиста вычислите: число 721₈ соответствует какому десятичному числу?

6. В системе счисления с основанием ______ десятичное число 26 записывается в виде 101.

Задачи (блок B)для выполнения:

1 – 10. Определить количество информации (по Хартли), содержащееся в системе, информационная емкость которой характеризуется десятичным числом Q. Закодировать это число по двоичной системе счисления, до двух цифр после запятой.

№	1	2	3	4	5	6	7	8	9	10
Q	500	1000	750	1250	250	1500	650	900	1100	1600

В статистической теории вводится энтропия как мера неопределенности случайного события. Если случайное событие имеет n элементарных исходов и известны их вероятности , то энтропия рассчитывается по формуле:

(4)

Размерность энтропии определяется основанием логарифма: при основании 2

энтропия измеряется в битах.

Определим количество информации, соответствующее i исходу, как

,

тогда энтропию можно определить как среднее количество информации, приходящееся на один исход,

.

Энтропия принимает максимальное значение в случае равновероятных исходов

, (5)

где n – число исходов.

Рассмотрим дискретный источник сообщений X. Пусть x_i – независимые элементы алфавита сообщений, а p(x_i) – их вероятности (i = 1, 2, …, n), тогда среднее количество информации на один элемент алфавита сообщений определяется через энтропию источника по формуле, аналогичной (4)

(6)

Максимальное количество информации соответствует случаю равных вероятностей элементов алфавита и определяется по формуле (5).

Определим абсолютную и относительную избыточность передаваемого сообщения по следующим формулам

, (7)

. (8)

Пример 2. Пусть в сообщении используются два независимых символа x₁ и x₂. Заданы вероятности появления символов р(x₁)=0,3 и р(x₂)=0,7.

Максимальное среднее количество информации на символ сообщения имеет место при равновероятном распределении и равно, согласно формуле (5),

(бит).

Рассчитаем среднее количество информации на символ сообщения при заданных вероятностях по формуле (6)

,

(бит)

Оценим избыточность сообщения по формулам (7) и (8)

(бит),

.

Задачи(блок С) для выполнения:

1–10. Определить среднее количество информации, содержащееся в сообщении, используемом три независимых символа S₁, S₂, S₃. Известны вероятности появления символов p(S₁)=p₁, p(S₂)=p₂, p(S₃)=p₃. Оценить избыточность сообщения.

№	1	2	3	4	5	6	7	8	9	10
p1	0,1	0,2	0,3	0,1	0,15	0,1	0,2	0,2	0,05	0,15
p2	0,15	0,1	0,15	0,3	0,2	0,4	0,25	0,3	0,15	0,25
p3	0,75	0,7	0,55	0,6	0,65	0,5	0,55	0,5	0,8	0,6