Часть 2. Дискретная математика. Структуры данных. Алгоритмы. Информатика.

1. Новиков 120-122; 128-130.

2.

4.1. Ограниченно-детерминированные функции

Пусть - конечное множество. Назовем это множество алфавитом, а его элементы – буквами.

Определение. Любая бесконечная последовательность элементов множества называется сверхсловом над алфавитом .

Для обозначения сверхслов используют запись , где .

Пусть и - множества сверхслов над алфавитами и соответственно. Рассмотрим функции, определенные на множестве и принимающие значения из .

Определение. Функция называется детерминированной, если для любого натурального числа и для любых сверхслов и из , у которых первые членов совпадают, верно, что в последовательностях и первые членов также совпадают (т.е. если …, , то и ).

Примеры.

1. Функция детерминированной не является.

2. Пусть . Функция является детерминированной.

3. Пусть . Рассмотрим функцию , такую что . Эта функция – детерминированная.

Пусть дан алфавит , . Рассмотрим бесконечное корневое ориентированное дерево, представленное на рисунке 1. Из корня этого дерева исходит пучок из дуг, образующих первый ярус. Каждая из дуг первого яруса ведет в вершину, из которой в свою очередь исходит пучок из дуг, образующих 2-ой ярус, и т.д. Вершины, являющиеся концами дуг яруса , причисляются также к ярусу . Вершина считается вершиной нулевого яруса. Упорядочим множество , после чего дуги каждого пучка пометим буквами алфавита слева направо согласно введенному порядку. Получим помеченное дерево .

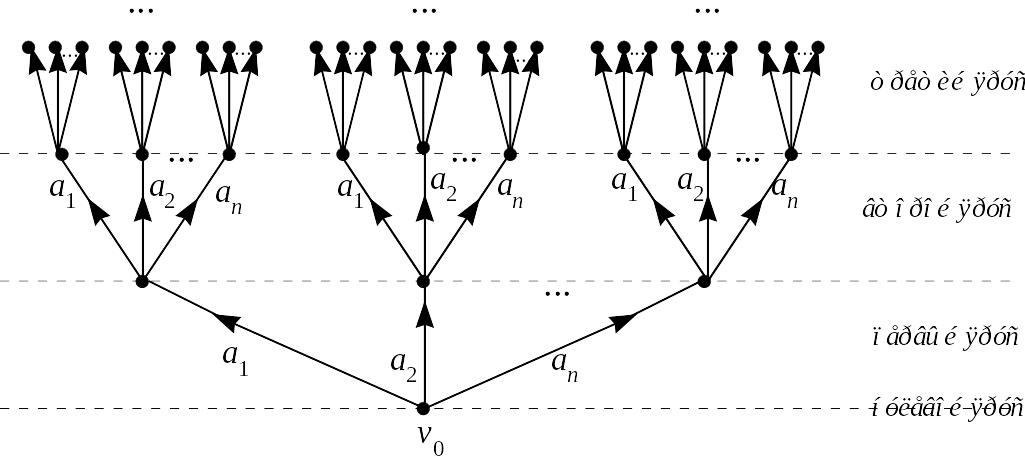Рис. 1

Бесконечный путь с началом в корне будем называть ветвью рассматриваемого дерева. Очевидно, что каждой ветви дерева можно поставить в соответствие последовательность букв – имен дуг, входящих в эту ветвь, если идти по ней, начиная от корня. И наоборот, любому сверхслову из однозначно соответствует некоторая ветвь дерева. Таким образом, существует взаимно-однозначное соответствие между множеством всех ветвей дерева и сверхсловами из .

На множестве вершин дерева введем бинарное отношение, которое определим следующим: . Это отношение является отношением эквивалентности и порождает разбиение множества вершин дерева на классы эквивалентности. Число различных классов эквивалентности по данному бинарному отношению, называется весом дерева, и соответственно, весом детерминированной функции.

Ограниченно-детерминированные функции

Определение. Детерминированные функции, имеющие конечный вес, называются ограниченно-детерминированными.

Для случая функции конечного веса на каждой ветке происходит повторение меток вершин, и индекс , определяющий усечение, удовлетворяет неравенству . Поэтому для этих функций усеченное дерево будет конечным. Таким образом, в случае ограниченно-детерминированной функции полное (бесконечное) информационное дерево можно всегда свести к конечному дереву, с дважды помеченными дугами и помеченными вершинами. Если в этом усеченном дереве произвести отождествление вершин с одинаковыми именами, а также отождествление кратных дуг с одинаковыми двойными метками, то получим так называемую диаграмму переходов ограниченно-детерминированной функции или, как ее еще называют, диаграмму Мура.

Пример 6. На рисунках 4 и 5 показаны усеченное дерево и диаграмма переходов функции из примера 2.

Рис. 4 Рис. 5

Рассмотрим диаграмму Мура произвольной ограниченно-детерминированной функции веса . Ее диаграмма Мура имеет вершин; из каждой вершины ( ) исходит дуг, дугам приписаны пары , , , где , - буквы алфавитов и соответственно; выделена начальная вершина.

Построим таблицу, строки которой соответствуют различным вершинам диаграммы Мура, а столбцы – различным буквам алфавита . Ячейки таблицы заполним по следующему правилу. Пусть ячейка, которую мы заполняем, соответствует вершине и букве . На диаграмме Мура отыщем дугу, с началом в вершине и первой меткой , после чего запишем в ячейку имя конца этой дуги и вторую метку самой дуги. Метку начальной вершины в заголовке строки выделим.

По сути, диаграммой Мура и таблицей автомата задаются две функции: функция , которая упорядоченной паре , ставит в соответствие , , и функция , которая упорядоченной паре , ставит в соответствие букву , .

Пример 7. Приведем таблицу для функции из примера 2.

	0	1
	1	0
	0	1

Пример 8. Приведем таблицу для функции из примера 3.

	0	1
	0	1
	0	0

И по диаграмме переходов и по таблице информационное дерево, а, значит, и сама ограниченно-детерминированная функция , восстанавливается однозначно. Опишем, как можно провести это восстановление. Возьмем помеченное дерево алфавита . Мы восстановим информационное дерево функции , если каждую дугу дерева пометим второй меткой. Вторые метки дуг будем расставлять пошагово: на первом шаге пометим дуги первого яруса, на втором - второго, и т.д. Нам будет проще, если мы на произвольном шаге будем помечать не только дуги, но и вершины яруса . Для удобства рассуждений для каждой ветви восстанавливаемого дерева введем в рассмотрение последовательность меток ее вершин.

Итак, нулевой шаг. Помечаем вершину нулевого яруса: присваиваем ей имя выделенной вершины диаграммы Мура , .

Шаг . К началу этого шага мы пометили дуги и вершины всех ярусов, начиная с нулевого и кончая ( )-ым. Возьмем произвольную дугу яруса ; пусть - ее первая метка, т.е. . Вершина, из которой эта дуга выходит, принадлежит ( )-му ярусу и, значит, ей уже дано какое-то имя , т.е. . На диаграмме Мура отыскиваем вершину с именем и выходящую из нее дугу с первой меткой . Пусть вершина - конец этой дуги, а - ее вторая метка. Тогда рассматриваемой дуге дерева даем вторую метку , т.е. , а ее концу даем имя , т.е. .

Таким образом, шаг за шагом информационное дерево функции будет восстановлено.

Заметим, что задать ограниченно-детерминированную функцию можно, указав правило, по которому каждой последовательности ставится в соответствие последовательность . Процедура восстановления информационного дерева функции по диаграмме Мура наводит на мысль, что, поскольку на каждом шаге восстановления однозначно определялось по и , то последовательность естественно задавать рекуррентно, используя при этом рекуррентное же задание последовательности .

Таким образом, приходим к следующим уравнениям:

Данные уравнения называются каноническими уравнениями ограниченно-детерминированной функции. По данным уравнениям ограниченно-детерминированная функция восстанавливается однозначно.

3.

4.

5.

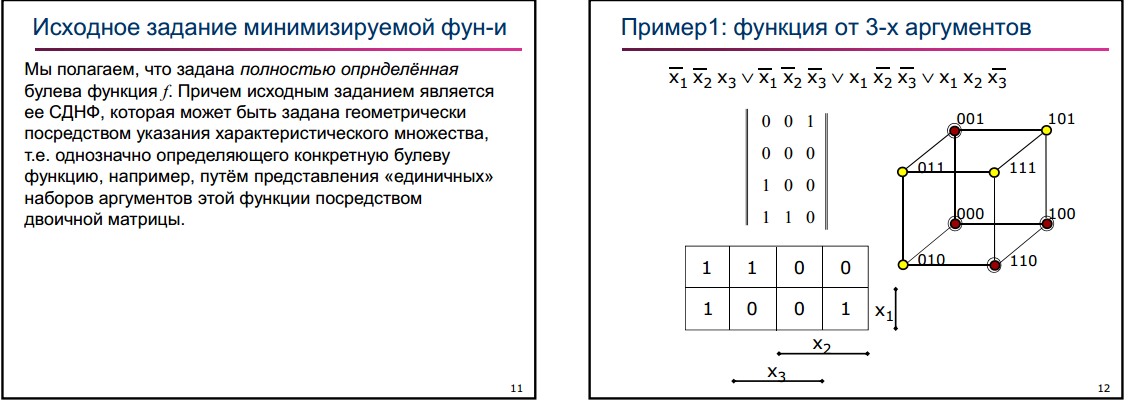
Определение 6.6. ДНФ называют минимальной, если она содержит наименьшее число литералов среди всех ДНФ, эквивалентных ей.

Обратим внимание на то, что под числом литералов в ДНФ понимают число всех подформул этой ДНФ, которые являются литералами. Так, СДНФ (6.9) содержит 12 литералов (по три литерала в каждой из четырех элементарных конъюнкции).

Пример 6.10. ДНФ   не является минимальной, так как ее можно преобразовать к эквивалентной ДНФ, не содержащей ни одного из литералов 

Вместо четырех литералов в исходной ДНФ получаем ДНФ, состоящую из одного литерала. Определение 6.7. Длиной ДНФ называют число входящих в нее элементарных конъюнкций. ДНФ называют кратчайшей, если она имеет наименьшую длину среди всех эквивалентных ей ДНФ.

Заметим, что кратчайшая ДНФ не обязана быть в то же время минимальной среди всех ДНФ, эквивалентных исходной функции. Но поиск минимальных ДНФ, как мы сейчас увидим, проводится среди кратчайших ДНФ.

Наша задача состоит в том, чтобы описать метод построения минимальной ДНФ, эквивалентной заданной булевой функции. Мы рассмотрим простейший метод такого рода, основанные на алгоритме Квайна — Мак-Клоски. Этот алгоритм исходит обязательно из СДНФ, которая строится по таблице функции так, как это было описано ранее.

5.

7.

8.

9.

10.

11.

12.