2.2. Ряд распределения хозяйств по расходу кормов на одну корову

После определения группировочного признака и границ групп строится ряд распределения.

Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Он характеризует состав (структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности.

Построим ряд распределения хозяйств по расходу кормов на одну корову. На первом этапе анализа расхода кормов на одну корову в какой-либо совокупности необходимо получить представление о ее вариации, изменчивости, а затем установить причины изменения и степени влияния факторов. Вариация, представляющая собой различие индивидуальных значений единиц совокупности, есть необходимое условие существования и развитие массовых явлений. В жизни общества, как и в природе, каждой массовой совокупности, массовому процессу присуща некоторая специфическая мера вариации ее элементов, при которой данный процесс протекает оптимально.

Для изучения вариации расхода кормов на одну корову используют ряд приемов: построение рядов распределения, расчет обобщающих показателей вариации, графическое изображение уровней, расчет показателей динамики и сравнения.

Ранжированный и интервальный ряды распределения строят для совокупности рассредоточенных в пространстве, сосуществующих в данный момент или период времени единиц. Ряд распределения показывает распределение единиц совокупности по какому-либо признаку в пространстве. Ряд распределения состоит из двух элементов (х - значения признака, f - частоты, веса).

Ряд распределения может быть дискретный (когда признак х – целое число) и интервальный (когда признак х – принимает значение интервала (от… до…)).

Ниже рассматривается интервальный ряд распределения хозяйств по расходу кормов на одну корову.

Признак (х), в данном случае, принимает значение интервала. Х – группы хозяйств по расходу кормов на одну корову, ц к. ед.

Число хозяйств f - частоты.

Интервалы групп можно определить, используя шаг определяемый по формуле 5.

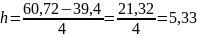
В первую группу [39,4-44,73] вошло 5 хозяйств, во вторую (44,73-50,06] – 11 хозяйств, в третью (50,06-55,39] - 10 хозяйств, в четвертую (55,39-60,72] – 6 хозяйств.

Таблица 5

Исходные данные распределения хозяйств по расходу кормов на одну корову.

Группы хозяйств по расходу кормов на одну корову, ц к. ед.	Численность хозяйств в группе, f			Кумулятивные (накопленные частоты), S
1) [39,4-44,73]	5	42,065	210,325	5
2) (44,73-50,06]	11	47,395	521,345	16
3) (50,06-55,39]	10	52,725	527,25	26
4) (55,39-60,72]	6	58,055	348,33	32
Итого	32	-	1607,25	-

По данным таблицы 5 видно, что наибольший удельный вес занимают хозяйства с средним показателем расхода кормов на одну корову (44,73-50,06]. На втором месте хозяйства с показателем в (50,06-55,39], таким образом можно сказать, что у подавляющего большинства хозяйств показатель расхода кормов на одну корову находится в промежутке (44,73-55,39].

Используя исходные данные таблицы, дадим оценку распределения хозяйств по расходу кормов на одну корову, используя структурные средние. Данные средней величины позволяют устранить влияние аномальных значений показателя.

Мода - это значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – вариант, имеющий наибольшую частоту.

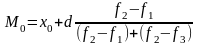(6)

где М₀ - мода;

х₀ - начало (нижняя граница) модального интервала (с наибольшей численностью);

d - величина модального интервала;

f₁ - частота интервала, предшествующего модальному;

f₂ - частота модального интервала;

f₃ - частота интервала, следующего за модальным.

Модальный интервал: (44,73-50,06]

Значит, в данной совокупности встречаются хозяйства, имеющие затраты корма на одну корову 49,29 ц к. ед..

Медиана – это вариант, который находится в середине вариационного ряда. Она делит ряд на две равные части – со значениями признака меньше медианы и со значениями признака больше медианы.

где М_е - медиана;

х₀ - нижняя граница медианного интервала;

d - величина медианного интервала;

åf – сумма частот ряда;

f_m - частота медианного интервала;

S_m-1 - сумма накопленных частот интервалов, предшествующих медианному.

Для того чтобы найти медианный интервал нужно определить номер медианы для четного объема совокупности:

В нашем случае медиана будет равна:

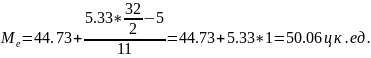
Это означает, что 50% хозяйств имеют затраты корма на одну корову менее чем 50,06 ц к. ед. и 50% хозяйств имеют затраты корма на одну корову более чем 50,06 ц к. ед..

Квартиль – это вид структурной средней величины, который делит изучаемую совокупность на четыре равные части. Определим номер квартиля в изучаемой совокупности:

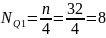
Квартильный интервал: (44,73-50,06]

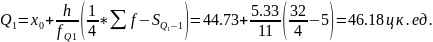
Аналогично определим квартиль третий:

(50,06-55,39] – это интервал для третьего квартиля.

.

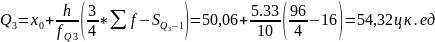Это означает, что 25% хозяйств имеют затраты корма на одну корову меньше, чем 46,18 ц к. ед., и 25% хозяйств имеют затраты корма на одну корову более чем 54,32 ц к. ед..

Дециль – это вид структурной средней величины, который делит изучаемую совокупность на 10 равных частей. Определим децильный интервал:

(39,4-44,73] – децильный интервал. Определим дециль первый:

Аналогично найдем дециль девятый. Для этого снова определим, какой из интервалов будет соответствовать децилю девятому.

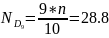
Это значение соответствует 4 интервалу (55,39-60,72], теперь найдем дециль девятый:

Это означает, что 10% хозяйств имеют затраты корма на одну корову менее чем 42,81 ц к. ед.. И 10 % хозяйств имеют затраты корма на одну корову более чем 57,87 ц к. ед..

Рассчитаем коэффициент децельной дифференциации затрат кормов на одну коров.

Значит, в 1,35 раз затраты корма на одну корову больше в 10% хозяйств в которых самый большой показатель затрат кормов на одну корову, чем в 10% хозяйств где этот показатель самый маленький.

Найдем Х_ср – среднее значение для ряда распределения.

Где 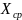- среднее значение для ряда распределения;

- средние значения х для каждой группы;

åf – общая сумма частот.

Значит среднее значение затраты кормов на одну корову в данной совокупности хозяйств составило 50,23 ц к. ед..

Проанализируем вариацию значений. Вариация – это различия значений признака у единиц совокупности. Вариацию значения признака Х можно определить с помощью коэффициентов абсолютной и относительной меры вариации.

Рассчитаем абсолютные показатели вариации.

Размах вариации – показывает вариацию в границах изучаемой совокупности.

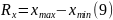
Где R_x- размах вариации;

X_max – максимальное значение признака Х;

X_min- минимальное значение признака Х.

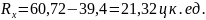
Квартильный размах вариации – показывает степень вариации значений признака Х в центре изучаемой совокупности.

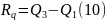
Где Rq – квартильный размах вариации;

Q₃- квартиль третий;

Q₁- квартиль второй.

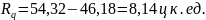
Для оценки степени вариации у совокупности единиц в целом используют среднее линейное отклонение.

Где x – анализируемый показатель;

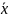- среднее значение анализируемого показателя;

f – частота.

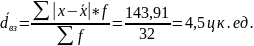
Найдем средний квадрат отклонения и среднее квадратическое отклонение.

Где 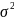- средний квадрат отклонения или дисперсия;

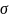- среднее квадратическое отклонение;

x – анализируемый показатель;

- среднее значение анализируемого показателя;

f – частота.

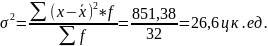
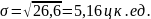
В данной совокупности хозяйств затраты корма на одну корову отклоняется от её среднего значения на 5,16 ц к. ед..

Рассчитаем относительные показатели вариации.

Рассчитаем коэффициент вариации.

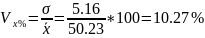
10 < 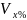< 30 => значит вариация умеренная, а совокупность более менее однородная.

Рассчитаем коэффициент осцилляции. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг общей средней.

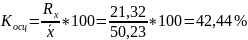
Найдем коэффициент относительного линейного отклонения, характеризующий долю усредненного значения абсолютных отклонений (модуль отклонений) от средней величины.