47, Прямолинейные образующие поверхностей второго порядка

Определение. Прямая, лежащая на поверхности, называется прямолинейной образующей этой поверхности.

Рассмотрим вопрос о том, имеют ли прямолинейные образующие изученные выше поверхности II порядка.

1.Так как эллипсоид – фигура ограниченная, заключенная в параллелепипеде

,

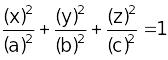то он не имеет прямолинейных образующих.

2. Рассмотрим двуполостный гиперболоид

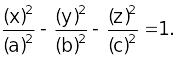
Изучая его методом сечений (см. Глава 11, § 107), было выяснено, что сечение поверхности плоскостью z = h при любом h не

содержит прямых линий. Поэтому гиперболический параболоид не имеет прямолинейных образующих, параллельных плоскости или лежащих в этой плоскости.

Если прямая не параллельна , не лежит в ней, то такая прямая пересекает плоскость z = h в некоторой точке, которая не лежит на нашей поверхности, так как двуполостный гиперболоид не имеет общих точек с . Следовательно, на нашей прямой есть точки, не принадлежащие поверхности, и поэтому такая прямая не может быть прямолинейной образующей двуполостного гиперболоида.

3. Аналогично можно показать, что у эллиптического параболоида нет прямолинейных образующих.

4. Прямолинейные образующие однополостного гиперболоида

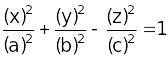: (1)

напоминают уравнение однополостного гиперболоида.

Преобразуем его:

,

. (1’)

Рассмотрим две системы уравнений:

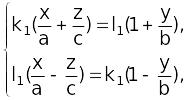(2)

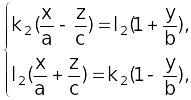(3)

где ,

.

Легко подсчитать, что в каждой из систем уравнений (3), (4) ранг матрицы, составленной из коэффициентов при x, y, z равен двум, то есть системы (3), (4) определяют прямую при фиксированных

Заметим, что если координаты некоторой точки удовлетворяют любой из систем уравнений (3), (4) (при фиксированных ), то они удовлетворяют уравнению (1’), а значит и (1), то есть .

Обратное тоже верно. То есть прямые, определяемые системами (3), (4) есть прямолинейные образующие однополостного гиперболоида.

Системы (3) и (4) при различных определяют два семейства прямолинейных образующих.

Свойства прямолинейных образующих однополостного гиперболоида.

1. Через каждую точку однополостного гиперболоида проходят две и только две прямолинейные образующие. Одна из них принадлежит семейству (3), а другая (4).

2. Любые две прямолинейные образующие одного семейства скрещиваются.

3. Любые две прямолинейные образующие из разных семейств лежат в одной плоскости.

4. Прямолинейные образующие гиперболического параболоида. Напомним, что уравнение гиперболического параболоида имеет вид:

(5)

или

(5’)

Рассмотрим 2 системы:

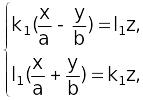(6)

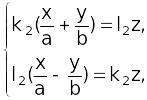(7)

где , .

Аналогично , однополостному гиперболоиду системы (6) и (7) определяют два семейства прямолинейных образующих гиперболического параболоида.

Замечание. Прямолинейные образующие гиперболического параболоида обладают свойствами 1 – 3., аналогичные свойствам однополостного гиперболоида.

Пример. Найти прямолинейные образующие однополостного гиперболоида

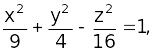
проходящие через точку

Решение.

Запишем уравнение в виде (1’).

.

Для 1 семейства имеем:

(*)

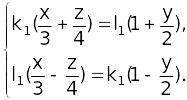Подставляя в (*) x = 6, y = 8, получим 2 , то есть можно, например, взять .

Подставляя эти значения в систему (*), имеем:

Эти уравнения определяют прямолинейные образующие, проходящие через точку и принадлежащие 1 семейству.

Аналогично системе (3) получили прямолинейные образующие 2 семейства, проходящие через точку .

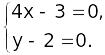
48. Поверхности вращения. Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d. Если уравнение поверхности в прямоугольной системе координат имеет вид: F(x² + y², z) = 0, то эта поверхность – поверхность вращения с осью вращения Оz. Аналогично: F(x² + z², y) = 0 – поверхность вращения с осью вращения Оу, F(z² + y², x) = 0 – поверхность вращения с осью вращения Ох. Запишем уравнения поверхностей вращения для некоторых частных случаев:

1. - эллипсоид вращения

2. - однополостный гиперболоид вращения

3. - двуполостный гиперболоид вращения

4. - параболоид вращения

Аналогично могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси Ох или Оу. Однако, перечисленные выше поверхности являются всего лишь частными случаями поверхностей второго порядка общего вида, некоторые типы которых рассмотрены ниже: 49. Цилиндрические поверхности. Определение. Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой. Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих:

1. - эллиптический цилиндр.

2) - гиперболический цилиндр.

2. x² = 2py – параболический цилиндр.

50. Конические поверхности второго порядка. Конические сечения

Определение. Конической поверхностью или конусом с вершиной в точке называется поверхность, которая вместе с каждой своей точкой М (М ) содержит и прямую . Прямые, проходящие через точку – вершину конуса, и лежащие на нем называются образующими конуса.

Замечание. Из определения конуса вовсе не следует, что он имеет единственную вершину.

Коническую поверхность можно получить следующим образом. Рассмотрим кривую и . Поверхность, образованная всеми прямыми, каждая из которых проходит через точку и через некоторую точку линии

, является конической.

Определение. Линия в этом случае называется направляющей конической поверхности.

Пусть направляющая задается уравнением

(1)

Образующие конической поверхности проходят через точку Напишем уравнение конической поверхности.

Пусть точка М(x, y, z) – произвольная точка поверхности S. Проведем образующую ; .

Так как ║ , то t =1 ; так как ( , ( , то

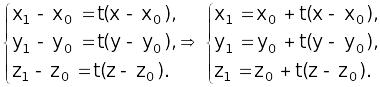(2)

Подставляя последние равенства в уравнения (1), получим:

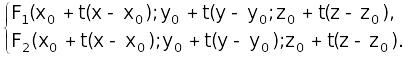
Выражая из последней системы t, получим уравнение конической поверхности.

Если направляющая – эллипс, то конус называется эллиптическим.

Пусть

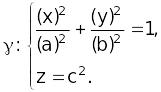– направляющая конуса.

– вершина конуса.

Составим уравнение конической поверхности S. Согласно (1), (2), имеем:

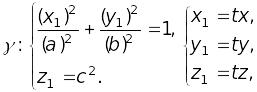
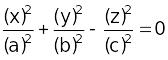– эллиптический конус.

Аналогично можно составить уравнения других конусов с различными направляющими.

Замечание. Если – окружность, то конус S называется круговым.

S: .

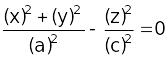Определение. Коническим сечением называется линия, по которой пересекаются круговой конус с произвольной плоскостью, не проходящей через его вершину.

Возможны 3 вида конических сечений.

По методу сечений.

1. Пусть плоскость сечения параллельна плоскости , то есть : z = h, тогда уравнение линии будет иметь вид:

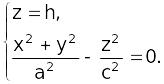
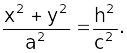
: , где .

Посмотреть

Окружность с центром в начале координат.

2.

;

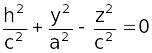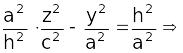
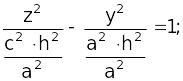
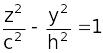– гипербола.

Посмотреть

Аналогично, для y = h получаем гиперболу.

Посмотреть

3. Рассмотрим плоскость, наклоненную под углом к . В сечении получаем либо параболу, либо эллипс.

51. Векторное п-мерное пространство, математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трёхмерного пространства.

Определение В. п. Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа (см. Векторное исчисление). В применении к любым векторам х, у, z и любым числам ,  эти правила удовлетворяют следующим условиям (условия А):

1) х + у = у + х (перестановочность сложения);

2) (х + у) + z = x + (y + z) (ассоциативность сложения);

3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x;

4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0,

5) 1 · х = х,

6) (x) = () х (ассоциативность умножения);

7) ( + ) х = х + х (распределительное свойство относительно числового множителя);

8) (х + у) = х + у (распределительное свойство относительно векторного множителя).

Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям А (условия 1—3 выражают, что операция сложения, определённая в В. п., превращает его в коммутативную группу). Выражение

₁e₁ + ₂e₂ + … + _ne_n (1)

называется линейной комбинацией векторов e₁, e₂,..., e_n с коэффициентами ₁, ₂,..., _n. Линейная комбинация (1) называется нетривиальной, если хотя бы один из коэффициентов ₁, ₂,..., _n отличен от нуля. Векторы e₁, e₂,..., e_n называются линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e₁, e₂,..., e_n равна нулевому вектору) векторы e₁, e₂,..., e_n называется линейно независимыми.

Векторы (свободные) трёхмерного пространства удовлетворяют следующему условию (условие В): существуют три линейно независимых вектора; любые четыре вектора линейно зависимы (любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми).

В. п. называется n-мepным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e₁, e₂,..., e_n, а любые n + 1 элементов линейно зависимы (обобщённое условие В). В. п. называются бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мepного В. п. образуют базис этого пространства. Если e₁, e₂,..., e_n — базис В. п., то любой вектор х этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов:

x = ₁e₁ + ₂e₂ +... + _ne_n.

При этом числа ₁, _2,..., _n называются координатами вектора х в данном базисе.

Примеры В. п. Множество всех векторов трёхмерного пространства образует, очевидно, В. п. Более сложным примером может служить так называемое n-мерное арифметическое пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел:  ₁,  ₂,...,  _n. Сумма двух векторов и произведение на число определяются соотношениями:

(₁, ₂, …, _n) + (₁, ₂, …, _n) = (₁ + ₁, ₂ + ₂, …, _n + _n);

(₁, ₂, …, _n) = (₁, ₂, …, _n).

Базисом в этом пространстве может служить, например, следующая система из n векторов e₁ = (1, 0,..., 0), e₂ = (0, 1,..., 0),..., e_n = (0, 0,..., 1).

Множество R всех многочленов ₀ + ₁u + … + _nuⁿ (любых степеней n) от одного переменного с действительными коэффициентами ₀, ₁,..., _n с обычными алгебраическими правилами сложения многочленов и умножения многочленов на действительные числа образует В. п. Многочлены 1, u, u²,..., uⁿ (при любом n) линейно независимы в R, поэтому R — бесконечномерное В. п.

Многочлены степени не выше n образуют В. п. размерности n + 1; его базисом могут служить многочлены 1, u, u²,..., uⁿ.

Подпространства В. п. В. п. R' называется подпространством R, если R'  R (то есть каждый вектор пространства R' есть и вектор пространства R) и если для каждого вектора v  r' и для каждых двух векторов v₁ и v₂ (v₁, v₂  R') вектор v (при любом ) и вектор v₁ + v₂ один и тот же независимо от того, рассматриваются ли векторы v, v₁, v₂ как элементы пространства R' или R. Линейной оболочкой векторов x₁, x₂,... x_p называется множество всевозможных линейных комбинаций этих векторов, то есть векторов вида ₁x₁ + ₂x₂ + … + _px_p. В трёхмерном пространстве линейной оболочкой одного ненулевого вектора x₁ будет, очевидно, совокупность всех векторов, лежащих на прямой, определяемой вектором x₁. Линейной оболочкой двух не лежащих на одной прямой векторов x₁ и x₂ будет совокупность всех векторов, расположенных в плоскости, которую определяют векторы x₁ и x₂. В общем случае произвольного В. п. R линейная оболочка векторов x₁, x₂,..., x_p этого пространства представляет собой подпространство пространства R размерности р. В n-мерном В. п. существуют подпространства всех размерностей, меньших р. Всякое конечномерное (данной размерности k) подпространство R' В. п. R есть линейная оболочка любых k линейно независимых векторов, лежащих в R'. Пространство, состоящее из всех многочленов степени  n (линейная оболочка многочленов 1, u, u²,..., uⁿ), есть (n + 1)-мepное подпространство пространства R всех многочленов.

52. Модели линейного векторного пространства