41. Поверхности второго порядка. Метод сечений

Определение. Поверхностью второго порядка называется множество всех точек пространства, координаты которых в какой-либо аффинной системе координат удовлетворяют алгебраическому уравнению второй степени:

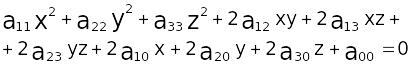, (1)

где – действительные числа, причем не все коэффициенты при членах второй степени равны нулю.

В изучении поверхностей второго порядка мы не будем исследовать уравнение (1) поверхности, а рассмотрим основные типы поверхностей, используя их простейшие (канонические) уравнения.

При этом мы будем использовать метод сечений, сущность которого состоит в следующем.

Пусть поверхность S задана в прямоугольной системе координат уравнением F(x,y,z)=0. Поверхность S пересекаем плоскостями, параллельными координатным плоскостям (или самими координатными плоскостями), и находим линии пересечения поверхности с этими плоскостями. По виду этих линий и выносится суждение о форме поверхности S. Применение метода сечений основано на следующей теореме.

Теорема 132. Пусть в прямоугольной системе координат заданы поверхность S уравнением (1) и плоскость , параллельная плоскости или совпадающая с ней, уравнением z = h. Если поверхность S пересекается с плоскостью по линии , то проекция линии на плоскость в системе координат имеет уравнение

F (x, y, h) = 0. (2)

Определение. Линия в пространстве ­– множество точек, принадлежащих двумерным поверхностям ψ и φ:

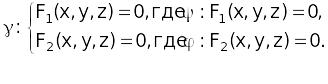
Примером линии может служить прямая, заданная пересечением двух плоскостей и

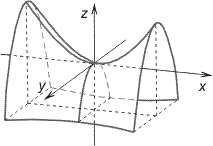
46. ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД

незамкнутая нецентральная поверхность второго порядка. В надлежащей системе координат (см. рис.) уравнение Г. п. имеет вид:

Сечения Г. п. плоскостями, параллельными плоскостям и , являются параболами, а сечения плоскостями, параллельными плоскости ,- гиперболами (плоскостью - двумя прямыми). Ось симметрии Т. п. наз. его осью; точка пересечения Г. п. с осью наз. вершиной Г. п. Если p = q, то Г. п. имеет две оси симметрии. Г. п.- линейчатая поверхность;

уравнения прямолинейных образующих, проходящих через данную точку Г. п., имеют вид:

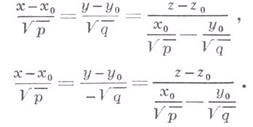
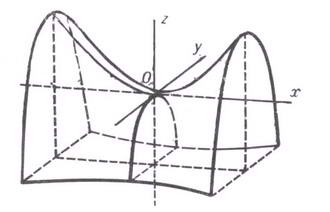
Гиперболический параболоид

Гиперболическим параболоидом называется поверхность второго порядка, заданная относительно специально выбранной прямоугольной системы координат уравнением: x²/p-y²/q=2z, p, q>0, p≥q (1). Если точка с координатами (x, y, z) лежит на гиперболическом параболоиде, то точки с координатами (±x, ±y, ±z) при любом наборе знаков также лежат на этой поверхности. Следовательно, плоскости xoy и yoz являются плоскостями симметрии гиперболического параболоида, а сечения, образованные данными плоскостями с поверхностью называются главными сечениями. Ось oz является осью симметрии гиперболического параболоида, если p≠q. Если p=q, то гиперболический параболоид имеет еще две оси симметрии, заданные уравнениями y=x, z=0 и y=-x, z=0. Вершиной гиперболического параболоида называется пересечение поверхности с oz. В данном случае вершиной поверхности является точка O(0, 0, 0).