1. Аффинная система координат (косоугольная система координат) — прямолинейная система координат в аффинном пространстве.
В
-мерном
пространстве она задаётся упорядоченной
системой линейно независимых векторов
,
выходящих из одной точки
.
Аффинными координатами точки
называют
такие числа
,
что
Tочку и систему векторов называют репером или аффинным базисом; прямые, проходящие через вектора — координатными осями.
На
аффинной плоскости
координату
называют
абсциссой,
а
—
ординатой
точки
.
В пространстве же координаты точки
называют её абсциссой, ординатой и
аппликатой.
Аналогичным образом именуют и координатные
оси.
ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ
Прямоугольная (или декартова) система координат в пространстве задается тройкой попарно перпендикулярных координатных осей, имеющих общее начало в точке О и одинаковый масштаб.
Оси координат в пространстве обычно обозначают Ох, Оу, Оz (оси абсцисс, ординат и аппликат соответственно).
В пространстве возможны правые (рис.)
и левые (рис.)
системы
координат; мы будем использовать правую
систему координат.
Орты осей Ох,
Оу,
Оz
— это единичные векторы
с
началом в точке О;
направления ортов совпадают с направлением осей.
Орты правой системы координат образуют правую тройку векторов.
Координатные плоскости хОу, уОz, хОz делят пространство на восемь октантов.
Координаты
х,
у,
z
точки Р
в пространстве определяются аналогично
координатам на плоскости:
это
координаты (на соответствующих осях)
оснований
перпендикуляров,
опущенных из точки Р
на оси Ох,
Оу,
Оz
, — соответственно абсцисса, ордината
и аппликата.
Координаты обычно указывают в
скобках:
Р(х;
у;
z).
Между точками в пространстве и
тройками их координат имеется взаимно
однозначное соответствие.
Расстояние между двумя точками
и
в
пространстве определяется с помощью
теоремы Пифагора:
В
частности, расстояние любой точки Р(х;
у;
z)
до начала координат равно
Координатами
вектора
в
прямоугольной системе координат Охуz
в пространстве называются его проекции
на координатные оси Ох,
Оу,
Оz:
.
Здесь α , β , γ — углы между вектором и
соответствующимиположительными
полуосями (рис.).
Вектор с координатами записывают в виде
или
.
При сложении векторов их соответствующие
координаты складываются, при умножении
вектора на число — умножаются на это
число:
.
Модуль вектора
вычисляется
по формуле
В
случае векторов на плоскости хОу
справедливы те же формулы, но отсутствует
третья координата; например,
Координаты
вектора
,
заданного двумя точками
и
равны
разностям соответствующих координат
точек А
и В:
,
т. е. чтобы найти координаты некоторого
вектора, достаточно из координат его
конца вычесть одноименные координаты
его начала.
Любой
вектор
на
плоскости может быть разложен
по ортам
прямоугольной
системы координат хОу:
.
Разложение по ортам
в
пространстве имеет вид
.
Векторные слагаемые
называются
составляющими
(или компонентами)
вектора
по
осям Ох,
Оу,
Оz.
Условие
коллинеарности двух векторов.
Два ненулевых вектора
и
коллинеарны
тогда и только тогда, когда их одноименные
координаты пропорциональны, т. е.
(1)
В равенстве (1) некоторые из знаменателей
могут оказаться равными нулю.
Условимся
всякую пропорцию
понимать
в смысле равенства
.
Например, равенства
означают,
что
,
т. е. что
.
В
случае векторов на плоскости условие
(1) принимает вид
(2)
Пусть
даны точки
и
.
Требуется найти точку М(х;
у;
z),
лежащую на отрезке
и
делящую его в данном отношении:
Очевидно,
что
или
Значит,
откуда
находим
(3)
Если
точки
и
принадлежат
плоскости хОу,
то в формулах (3) третья координата
отсутствует.
2. Расстояние между двумя точками. Деление отрезка в данном отношении
Расстояние
d между двумя точками
(
,
,
)
и
(
,
,
)
в пространстве определяется формулой
.
Координаты
x, y, z точки М, которая делит отрезок
,
ограниченный точками
(
,
,
)
и
(
,
,
),
в отношении
,
определяется по формулам
,
,
.
В
частности, при
имеет
координаты середины данного отрезка:
,
,
.
18. Прямая в пространстве. Различные способы задания прямой в пространстве. Уравнение прямой заданной точкой и направляющим вектором.
Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.
Итак,
если уравнения двух непараллельных
плоскостей --
и
,
то прямая, являющаяся их линией
пересечения, задается системой уравнений
|
(11.11) |
И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.
Уравнения (11.11) называют общими уравнениями прямой в пространстве.
Замечание 11.2 Любые попытки с помощью преобразований уравнений системы (11.11) получить одно (линейное) уравнение, задающее прямую, обречены на неудачу. Одно уравнение -- это уравнение плоскости.
Общие уравнения прямой "неудобны" для получения информации о положении прямой.
Например, чтобы найти координаты какой-нибудь точки на прямой, нужно провести довольно сложные вычисления. А именно, задать произвольно какую-нибудь координату, подставить ее в систему (11.11) и из получившейся системы двух уравнений с двумя неизвестными найти две остальные координаты. Причем может оказаться, что полученная система не имеет решений. Тогда нужно произвольно задать другую координату и из системы найти две оставшиеся координаты.
Пример
11.2
Требуется найти какую-нибудь точку
на
прямой
Решение.
Положим
.
Получим систему
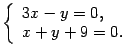
Решая
ее, находим
,
.
Ответ:
.
Можно задать прямую в пространстве и другим способом.
Ненулевой вектор, лежащий на прямой (параллельный ей) называется направляющим вектором прямой.
Пусть
для прямой
известны
ее направляющий вектор
и
точка
,
лежащая на этой прямой. Пусть
--
произвольная (текущая) точка прямой
.
Обозначим через
и
r
радиус-векторы точек
и
соответственно
(рис. 11.11).
Рис.11.11.Векторное уравнение прямой
Тогда
вектор
коллинеарен
вектору p
и, следовательно,
,
где
--
некоторое число. Из рис. 11.11 видно, что
|
(11.12) |
Это уравнение называется векторным уравнением прямой или уравнением в векторной форме. При каждом значении параметра мы будем получать новую точку на прямой .
Замечание
11.3
Если в качестве параметра
взять
время, то точка
будет
двигаться по прямой со скоростью
,
причем в момент времент
ее
положение совпадает с точкой
.
Вектор скорости точки совпадает с
вектором p.
От
векторного соотношения (11.12)
перейдем к соотношениям координат. Так
как
--
координаты точки
,
то
,
,
.
Из формулы (11.12)
получим
|
(11.13) |
Полученная система уравнений называется параметрическими уравнениями прямой.
Обратим внимание на то, что по параметрическим уравнениям легко установить направляющий вектор прямой и координаты одной из ее точек. Коэффициенты перед параметром дают координаты направляющего вектора, а свободные члены в правой части -- координаты точки на прямой.
Так как направляющий вектор прямой определяется с точностью до умножения на число, отличное от нуля, а в качестве точки можно взять любую точку прямой, то одна и та же прямая может задаваться бесконечным множеством систем параметрических уравнений. Причем разные системы могут быть не похожими друг на друга.
Из уравнений (11.13) выразим параметр :
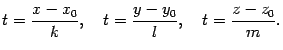
Так как во всех трех соотношениях параметр имеет одно и то же значение, то
|
(11.14) |
Эти уравнения называются каноническими1 уравнениями прямой.
Замечание
11.4
В канонических уравнениях прямой
допускается в знаменателе писать 0. Это
не означает, что можно выполнить деление
на 0. Просто из канонических уравнений
мы получаем информацию о том, что
направляющий вектор прямой имеет
координаты
,
из которых одна нулевая.
Пример 11.3 Прямая с каноническими уравнениями
имеет
направляющий вектор
.
Замечание 11.5 Канонические уравнения прямой (11.14) нельзя рассматривать как одно уравнение (в них два знака "=" и следовательно, два уравнения). Они составляют своеобразным способом записанную систему из двух уравнений
Возможны, впрочем, еще две записи системы, подумайте какие.