Изохорный процесс
Изохорный процесс происходит при нагревании или охлаждении газа в постоянном объеме. Это может быть цилиндр с неподвижным поршнем или резервуар постоянного объема.
Уравнение изохорного процесса υ = const. Соотношение между параметрами состояния в изохорном процессе в соответствии с законом Шарля для идеальных газов
р1/Т1 = p2/T2.
В рυ-координатах изохорный процесс изображают отрезком прямой, параллельной оси ординат (рисунок 3.4).
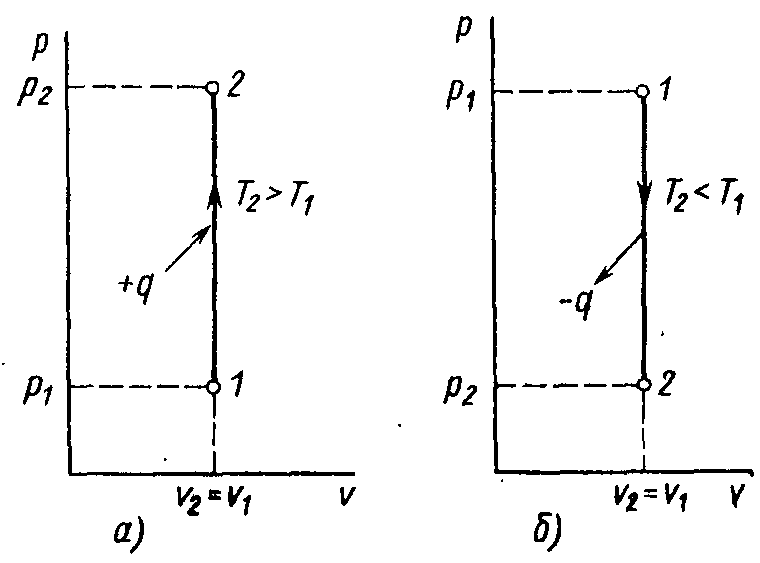
а – с подводом теплоты; б – с отводом теплоты
Рисунок 3.4 – Диаграмма изохорного процесса
При нагревании газа его давление и температура повышаются, а при охлаждении – уменьшаются. Механическая работа газа а в изохорном процессе равна нулю, так как нет изменения объема:
υ = const; dυ = 0;
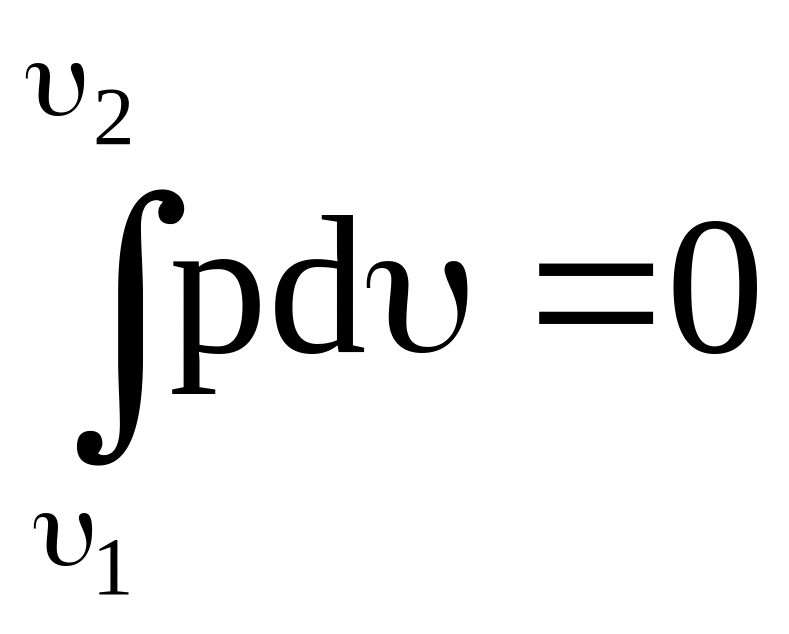
По первому закону термодинамики теплота изохорного процесса
q = Δu + a = Δu
Так как a = 0, то подводимая к газу теплота идет на изменение его внутренней энергии. Поэтому в изохорном процессе с подводом теплоты внутренняя энергия газа, а следовательно, и его температура повышаются, а в процессе с отводом теплоты – снижаются. Принимая теплоемкость тела не зависящей от температуры, теплота q изохорного процесса
q = cυ(T2 – T1).
Из последнего равенства следует, что изменение внутренней энергии
Δu = u2 – u1 = cυ (Т2 – T1).
Так как изменение внутренней энергии не зависит от характера процесса, то по данной формуле можно определять изменение внутренней энергии в любом термодинамическом процессе.
Изобарный процесс
Изобарный процесс происходит при нагревании или охлаждении газа с постоянным давлением. Такой процесс может быть получен в цилиндре с поршнем, на который действует постоянная нагрузка. Уравнение изобарного процесса р = const. При изобарном подводе теплоты объем газа и его температура увеличиваются, при отводе – уменьшаются. По закону Гей-Люссака изменение объема газа в процессе с постоянным давлением прямо пропорционально изменению его абсолютной температуры, т. е.
υ2/υ1 = Т2/Т1
Изменение внутренней энергии в изобарном процессе
Δu = cυ(Т2 – Т1)
Уравнение изобарного процесса. В рυ-координатах изобарный процесс изображается отрезком прямой, параллельной оси абсцисс (рисунок 3.5).
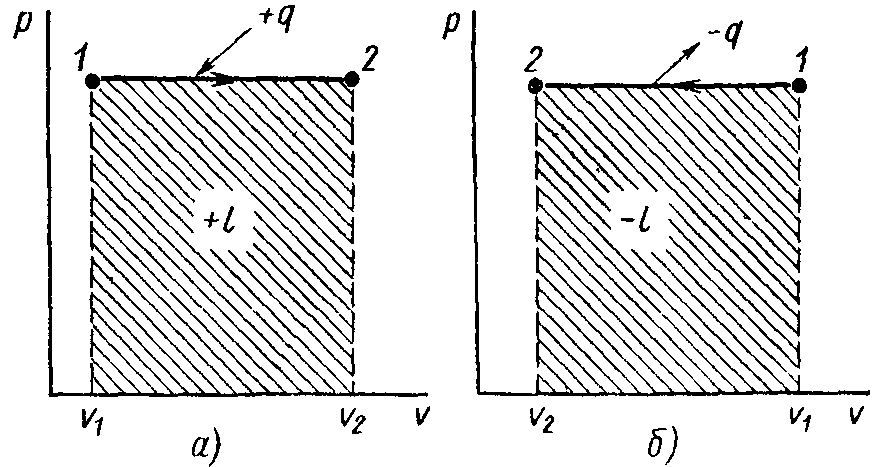
а – с подводом теплоты; б – с отводом теплоты
Рисунок 3.5 – Диаграмма изобарного процесса
Работа газа в изобарном процессе
a = р(υ2 – υ1) = R(T2 – T1),
так как по уравнению состояния pυ = RT.
Учитывая, что р2 = р1 располагаемая работа a в изобарном процессе
ao = υ(p2 -– p1) = 0.
Теплота, необходимая для совершения процесса, по первому закону термодинамики
q = Δu + a = Сυ(Т2 – Т1) + R(T2 – T1) = ср(Т2 – T1).
Сравнивая выражения для определения изменения внутренней энергии
Δu = cυ(T2 – T1) и теплоты q = ср (Т2 – T1), можно определить долю теплоты α, затрачиваемую на изменение внутренней энергии, и 1 – α, затрачиваемую на совершение механической работы:
α = Δu/q = cυ(T2 – T1)/cp(T2 – T1) = 1/k
1 – α = (k – 1)/k
Из этих соотношений следует, что с увеличением атомности газа, т. е. с уменьшением k доля теплоты, превращаемой в механическую работу, уменьшается, так как доля теплоты, идущей на изменение внутренней энергии, увеличивается.