Энтальпия

В термодинамике важную роль играет сумма внутренней энергии системы U и произведения давления системы р на ее объем V, называемая энтальпией и обозначаемая Н:

Н = U + pV

Так как входящие в нее величины являются функцией состояния, то и сама энтальпия является функцией состояния.

Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).

Энтальпия обладает свойством аддитивности. Величина

h = u + pυ

называемая удельной энтальпией (h = H/M), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.

Поскольку энтальпия есть функция состояния, то она может быть представлена в виде функции двух любых параметров состояния:

h = ψ₁ (p, υ); h = ψ₂(υ, T ); h = ψ₃(p, T),

а величина dh является полным дифференциалом.

Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от характера процесса.

Физический смысл энтальпии выясним на следующем примере. Рассмотрим расширенную систему, включающую газ в цилиндре с поршнем с грузом общим весом G (рисунок 3.3).

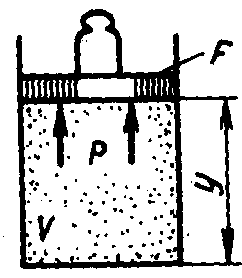
Рисунок 3.3 – К определению физического смысла энтальпии

Энергия этой системы складывается из внутренней энергии газа и потенциальной энергии поршня с грузом в поле внешних сил:

Е = U + Gy

В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа:

E = U + pFy = U + pV.

Получаем, что Е = Н, т.е. энтальпию можно трактовать как энергию расширенной системы.

Уравнение δq = du + pdυ в случае, когда единственным видом работы является работа расширения, с учетом очевидного соотношения

pdυ = d(pυ) – υdp

может быть записано в виде

δq = d(u + pυ) – υdp

или

δq = dh – υdp

Из этого соотношения следует, что если давление системы сохраняется неизменным, т.е. осуществляется изобарный процесс (dp = 0), то

δq = dh

q_p = h₂ – h₁

т.е. теплота, подведенная к системе при постоянном давлении, идет только на изменение энтальпии данной системы.

Для идеального газа

dh = du + d(pυ) = c_pdT + RdT = (c_υ + R)dT = c_pdT

Так как между энтальпией и внутренней энергией существует связь (h = u + pυ), выбор начала отсчета одной из них не произволен: в точке, принятой за начало отсчета внутренней энергии, h = pυ.

Например, для воды при t = 0,01 ºС и р = 610,8 Па, U = 0, а h = pυ = 610,8·0,001 = 0,611 Дж/кг.

При расчетах практический интерес представляет изменение энтальпии в конечном процессе:

.

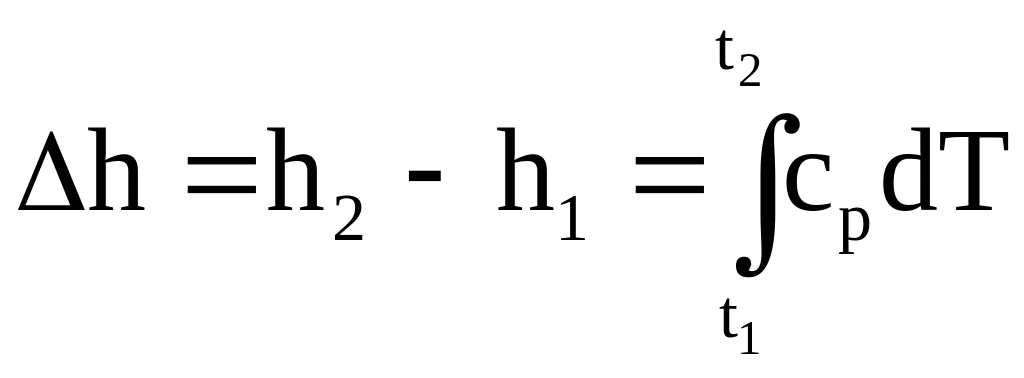Состояние рабочего тела в каждый момент термодинамического процесса должно удовлетворять уравнению состояния идеального газа. Соотношение между теплотой процесса, изменением внутренней энергии рабочего тела и совершаемой или получаемой им работой должно соответствовать первому закону термодинамики. Поэтому исследование термодинамических процессов базируется на уравнениях состояния идеального газа и первого закона термодинамики.

Необходимо составить уравнение термодинамики термодинамического процесса, установить характер изменения внутренней энергии в процессе, получить математические выражения для определения механической и располагаемой работы процесса, а также количества внешней теплоты, подводимой или отводимой в процессе. Для каждого процесса устанавливают соотношение между параметрами состояния в начале и конце процесса и представляют графическое изображение в рυ-координатах. Графики основных термодинамических процессов соответственно называются изохорой, изобарой, изотермой, адиабатой и политропой.