Лекція 8

План лекції:

• Бульові (логічні) похідні;

• Метод активізації шляхів

8 Побудова тестів перевірки дискретних пристроїв методом активізації шляхів

8.1 Бульові (логічні) похідні

Для забезпечення бачності несправності може бути використаний апарат бульових похідних.

Бульові (логічні) похідні, подібно звичайним похідним, зв'язують зміни функції зі змінами її аргументів. Розглянемо похідні одного аргументу.

Бульова похідна від логічної функції на деякому наборі дорівнює 1, якщо зміна значення змінної x_i на протилежне приводить до зміни функції, у противному випадку .

Приклад 8.1 На Рис.8.1 показано карти Карно деякої функції (а) і похідних (б), (в), (г). Як видно,

Рис.8.1 Карти Карно функції F(x₁,x₂,x₃) і її похідних

Карти Карно на Рис.8.1,д,е,ж пояснюють, як можна знайти похідні . Варто виділити усі пари кліток, що є суміжними для змінної x_i. Якщо значення в парі кліток збігаються, то значення похідної в цих клітках дорівнюють 0, у супротивному випадку вони дорівнюють 1.

З цього способу обчислення похідної ясно, по-перше, що вона не завжди залежить від змінної x_i. По-друге, неважко установити, що , тобто похідні від функції і її заперечення збігаються. Також збігаються похідні від функції F за змінною x_i і її запереченню .

На підставі викладеного можна дати узагальнене визначення бульової похідної як

(8.1)

де отримують з F прирівнюванням змінної x_i відповідно нулеві й одиниці.

П риклад 8.2. Нехай (див. Рис.8.2,б). Тоді

Рис.8.2 Приклад логічної схеми і карти Карно до неї

Вираз (8.1) можна записати і трохи інакше

(8.2)

де отримують з F заміною x_i. на і на x_i..

Появу несправності в точці схеми, у якій повинен діяти сигнал , можна розглядати як зміну змінної Z. Для з'ясування питання про бачність несправності варто описати вихідну змінну Y як функцію вхідних змінних і змінної й обчислити похідну . На всіх наборах, де , несправність проявиться на виході схеми.

Приклад 8.3. Для схеми (див. Рис.8.2, а) у випадку несправності на нижньому вході елемента 3 маємо

. (8.3)

Представляючи цю функцію картою Карно (Рис.8.3,а), знаходимо похідну: (Рис.8.3, б).

Р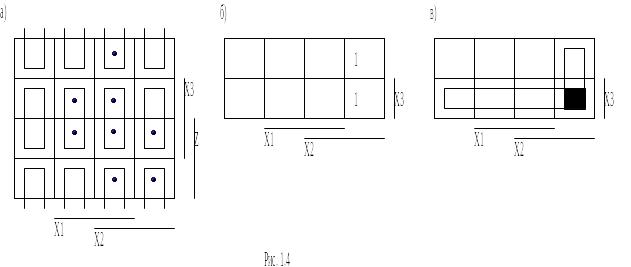 ис.8.3 Карти карно функції (8.3) і її похідної за змінною Z

Одночасне виконання умов керованості і бачності можна записати тепер у виді кон’юнкції де , якщо С=0, інакше . Несправність може бути виявлена на кожному з наборів, що задовольняють рівнянню

(8.4)

Іноді це рівняння записують інакше

(8.5)

У випадку несправності більш загального виду, ніж константна, коли сигнал у підозрюваній точці описується перекрученою (оберненою) функцією , вираз (8.5) прийме вид

(8.6)

У будь-якому випадку у виразах (8.4), (8.5), (8.6) перший співмножник описує умови керованості, другий - умови бачності.

8.2 Метод активізації шляхів

Використовуючи термін «транспортування несправностей», мають на увазі бачність несправності на виходах ЦП. При цьому мають на увазі, що у схемі можна виділити ланцюжок елементів від місця підозрюваної несправності до виходу (або до контрольної точки), стан яких однозначно визначається наявністю (відсутністю) несправності.

Приклад ланцюжка елементів показаний на рис. 8.4. Очевидно, що транспортування несправності буде забезпечене лише за умови, що у всіх ланках ланцюжка зміна Z_i обов'язково спричинить зміну , тобто для всіх m елементів:

.

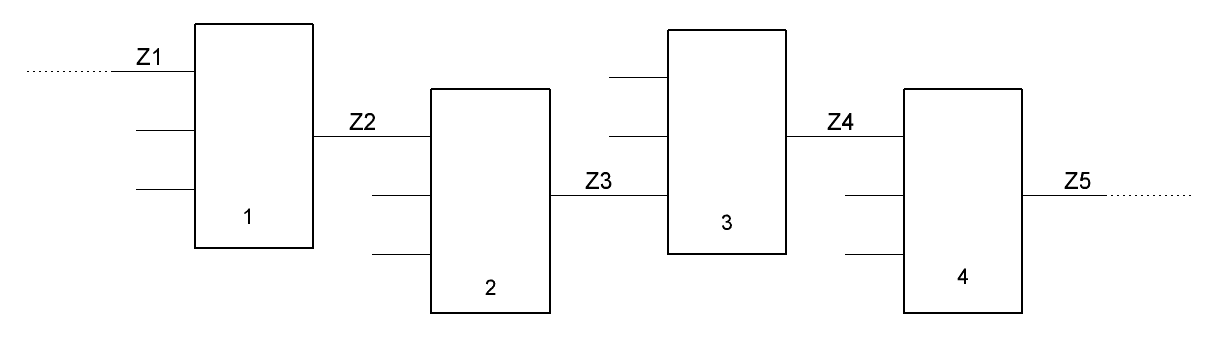
Рис.8.4 Приклад ланцюжка елементів

Очевидно також, що умова для кожного елемента буде виконана, якщо на інші входи цього елемента будуть подані відповідні логічні сигнали. Ця умова забезпечується відповідним набором вхідних сигналів.

Задача побудови тесту для ЦП за розглянутим методом, власне, і полягає в тому, щоб для кожної несправності знайти в схемі транспортуючий ланцюжок, визначити необхідні стани елементів ланцюжка і підібрати такий вхідний набір, що забезпечує ці стани.

Коли ланцюжок побудований, говорять, що знайдено активізований (істотний, чуттєвий) шлях.

Щоб вирішувати такі задачі, необхідно насамперед навчитися транспортувати несправності через окремі, для початку - найпростіші елементи, що ми і розглянемо нижче.

Відмітимо декілька попередніх тверджень:

• забезпечити чутливість виходу елемента до зміни на деякому його вході логічного рівня з 0 на 1 (з 1 на 0) - значить одночасно забезпечити і перевірку несправності C на цьому вході (а також на виході попереднього елемента, що зв'язаний з цим входом);

• будуючи ланцюжок для транспортування несправності, наприклад, із входу елемента 1 (див. рис. 8.4), ми тим самим забезпечуємо транспортування відповідних несправностей і з виходу елемента 1, із входу елемента 2 і т.д.;

• знайти умови транспортування логічних рівнів 0 і 1 через усі входи елемента на його вихід - значить знайти тест для цього елемента, повний щодо безлічі всіх ОКН на його входах і виході.

Для логічних елементів тести будуються легко шляхом розв’язання рівняння (8.4).

Для n-входового елемента додавання за модулем 2 (М2) на всіх наборах. Тому два набори 00...0 і 11...1 перевіряють всі ОКН на входах. Якщо n парне, то додатково потрібно подати ще набір, що містить непарне число одиниць, для перевірки на виході. Для двовходового елемента М2 повним тестом можуть служити, наприклад, набори 00, 01, 11.

Несправності зовнішніх входів і виходу (виходів) елемента називають іноді контактними несправностями. Якщо деякий елемент, наприклад елемент М2 (рис. 8.5) побудований з найпростіших елементів, то повнота тесту щодо контактних несправностей ще не гарантує перевірки усіх внутрішніх ОКН.

Частина внутрішніх ОКН, звичайно, виявляється при транспортуванні контактних несправностей із входів на вихід. Виникає питання про те, чи усі несправності комбінаційної схеми потрібно розглядати, щоб забезпечити повноту тесту? Виявляється, досить розглянути множину характеристичних несправностей, тобто ОКН зовнішніх входів (контактних ОКН) і ОКН у всіх ланках розгалуження.

Наприклад, для схеми (див. рис. 8.5) досить розглянути ОКН у точках 1,2,3,4,6,7,8,9.

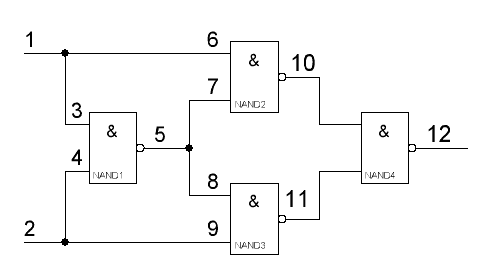
Рис.8.5 Схема, що реалізує функцію додавання за модулем 2

Розглянемо табл. 8.1, у якій представлені функції, що реалізуються схемою (див. рис. 8.5) при ОКН у всіх пронумерованих точках. Таблиці такого роду називають таблицями функцій несправностей (ТФН).

Таблиця 8.1

Набір 2 1	Справна схема	Номер точки характер несправності 1 2 3 4 5 6 7 8 9 10 11 12 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
0 0 0 1 1 0 1 1	0 1 1 0	0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 1 0 0 1 0 1 1 0 1 1 1 0 0 1 0 1 0 1 1 1 1 1 1 0 1 1 0 1 1 0 0 1 1 0 1 1 0 1 1 1 1 1 0 1 0 0 1 1 1 0 0 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 0 1

Рядки ТФН можуть відповідати і не усім вхідним наборам, а лише включеним у тест. Перевага ТФН полягає в їхній універсальності - вони можуть бути складені для будь-якого типу логічних несправностей, а не тільки константних.

Недолік ТФН - їхня громіздкість, так що практично вони можуть бути складені тільки для невеликих схем.

Для відшукання мінімального повного тесту по ТФН на основі останньої будують бульову матрицю, обчислюючи суму за модулем 2 стовпця кожної несправності зі стовпцем справної схеми. Для матриці знаходять найкоротше рядкове покриття. Набори, що відповідають рядкам, які ввійшли в покриття, складають мінімальний тест.

Приклад 8.2. За табл. 8.1 побудуємо бульову матрицю:

1 2 3 4 5 6 7 8 9 10 11 12

Усі рядки цієї матриці - обов'язкові. Покриття складається з усіх рядків, тест включає всі можливі набори (такий тест називають тривіальним). Зверніть увагу на те, що стовпці всіх несправностей, що не відносяться до характеристичних, поглинаються іншими стовпцями, тобто свідомо не впливають на склад покриття.

Контрольні запитання

1. Дайте визначення бульової похідної.

2. Поясніть порядок визначення бульової похідної за картою Карно.

3. У якому випадку процес тестування цифрової схеми вважають керованим?

4. Що розуміють під терміном «транспортування несправностей»?

5. Що є умовою транспортування несправностей?

6. Що таке активізований шлях?

7. Які несправності називають контактними?

8. Які несправності називають характеристичними?

9. Що виражає таблиця функцій несправностей (ТФН)?

10. Для чого формують бульову матрицю за ТФН?

Завдання на самостійну роботу

1. Дайте відповіді на контрольні запитання.

2. Нанесіть на карти Карно похідні функції (див. Рис.8.2,б).