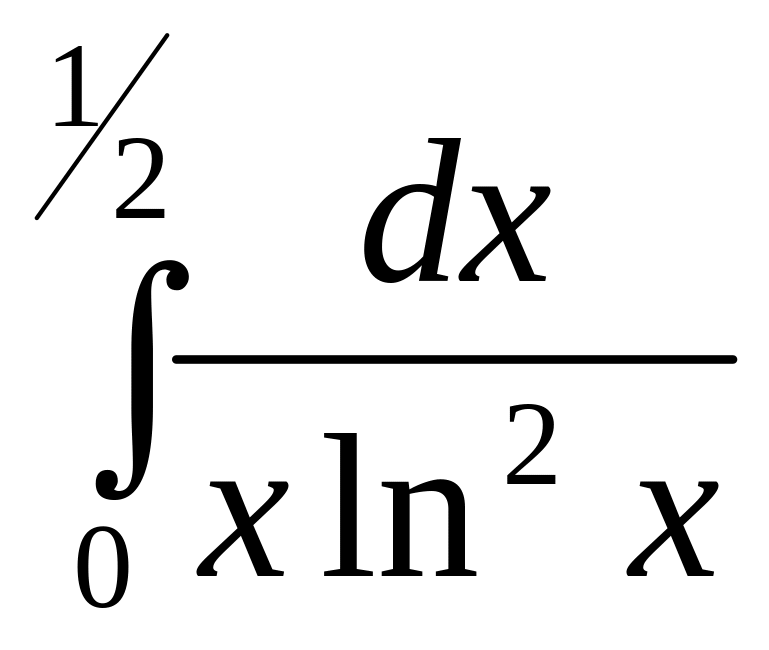Zavd_dlya_pidgot_do_ekzamenu_2011-2012_2_semest

Питання

для пiдготовки до екзамену 2008-2009 (стаціонар, 2 семестр)

1. Границя числової послідовності. Основні властивості числових послідовностей.

2. Нескінченні границі. Число е. Натуральні логарифми.

3. Границя функції в точці. Однобічні границі. Границя функції на нескінченності. Нескінченно велика функція.

4. Нескінченно малі величини і їх властивості. Порівняння нескінченно малих великих.

5. Основні теореми про границі. Розкриття деяких невизначеностей при знаходженні границь. Дві важливі границі.

6. Властивості неперервних функцій (основні теореми).

7. Застосування похідної до дослідження функцій.

8. Еластичність функції, її властивості.

9. Еластичність попиту від ціни, граничний дохід.

10. Поняття функції кількох змінних. Основні поняття. Відкриті та замкнені множини. Означення функції кількох змінних. Область визначення та множина значень.

11. Частинні прирости і частинні похідні першого порядку.

12. Повний приріст і повний диференціал.

13. Частинні похідні і повні диференціали вищих порядків.

14. Екстремум функції кількох змінних.

15. Використання критерію Раусса-Гурвіца для дослідження екстремуму функції.

16. Поняття первісної функції та невизначеного інтеграла. Основні властивості первісної та невиз­наченого інтеграла.

17. Таблиця основних інтегралів та перевірка їх правильності. Основні правила інтегрування.

18. Безпосереднє інтегрування та інтегрування заміною змінної.

19. Інтегрування частинами. Основні типи інтегралів, що інтегруються частинами.

20. Визначений інтеграл. Обчислення площі криволінійної трапеції.

21. Основні властивості визначеного інтеграла.

22. Інтеграл із змінною верхньою межею інтегрування. Формула Ньютона-Лейбніца.

23. Заміна змінної та інтегрування частинами у визначеному інтегралі.

24. Невласні інтеграли з нескінченими межами та від необмежених функцій.

25. Основні поняття диференціальних рівнянь. Задача Коші.

26. Диференціальні рівняння з відокремлюваними змінними.

27. Однорідні диференціальні рівняння першого порядку.

28. Лінійні диференціальні рівняння першого порядку.

29. Лінійні однорідні диференціальні рівняння другого порядку з сталими коефіцієнтами. Знаходження загального розв’язку.

30. Лінійні неоднорідні диференціальні рівняння другого порядку з сталими коефіцієнтами. Знаходження частинного розв’язку методом варіації сталих.

31. Неперервність функцій. Два означення неперервності функції.

32. Розриви функції. Класифікація точок розриву функції.

33. Похідна за напрямом. Градієнт.

34. Теорема про середнє значення.

Завдання до екзамену з курсу

„Математика для економістів ”

Знайти границю послідовності:

1. ;

2. ;

3. ;

4. ;

5. ;

6. 

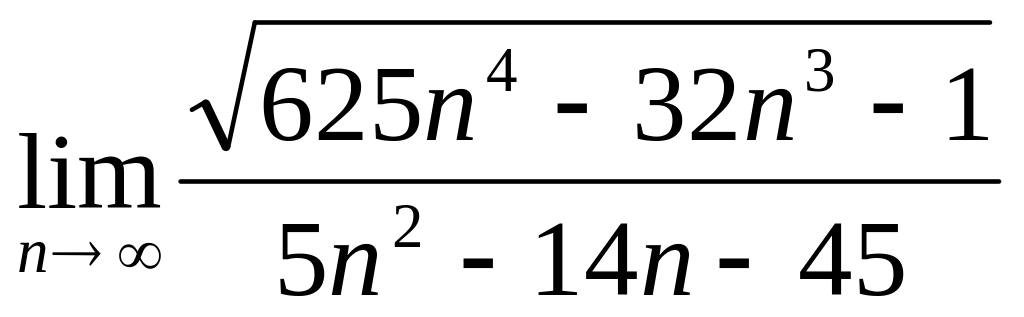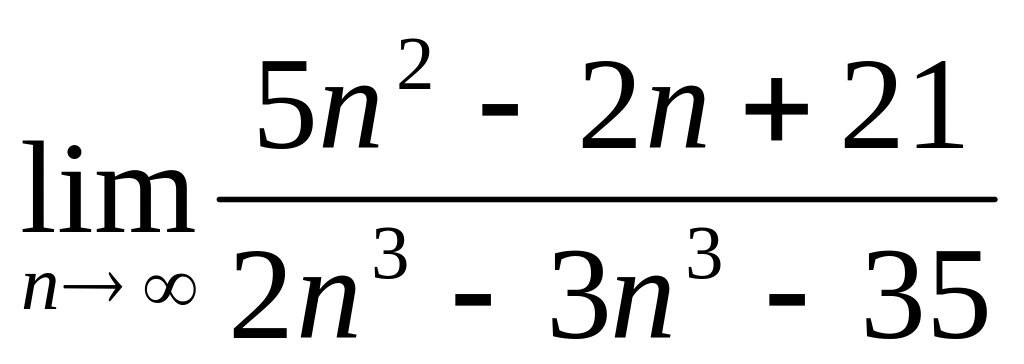Обчислити границі, застосувавши правило Лопіталя:

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. .

17. ;

18. 

19. ;

20. ;

21. 

22. ;

23. ;

24. ;

25. 

26. ;

27. ;

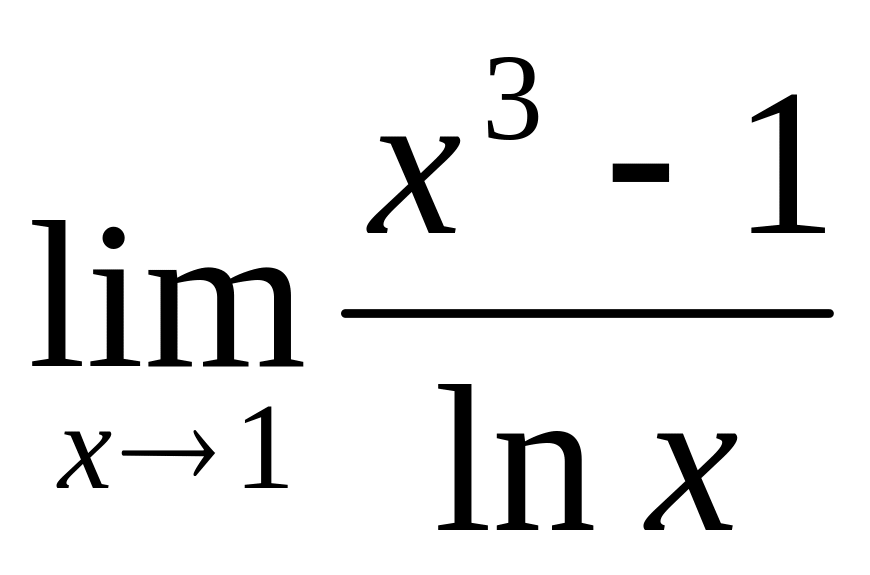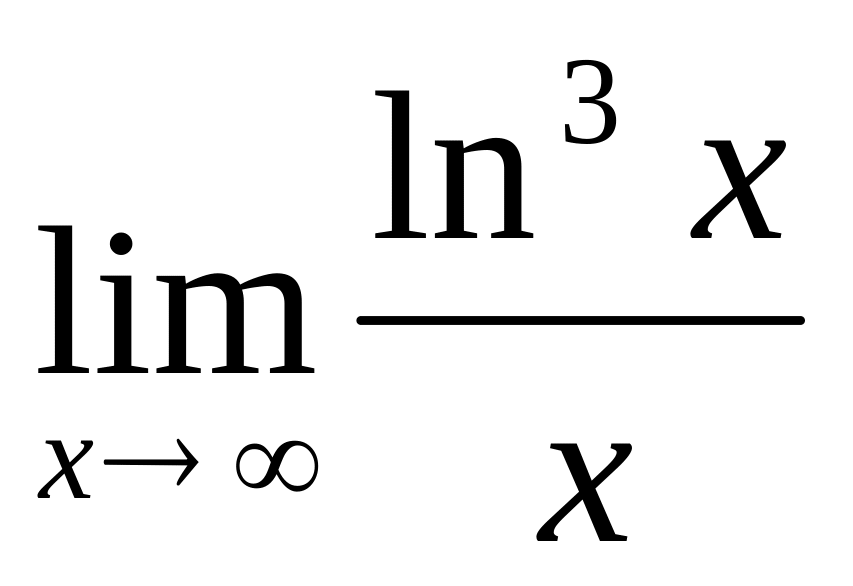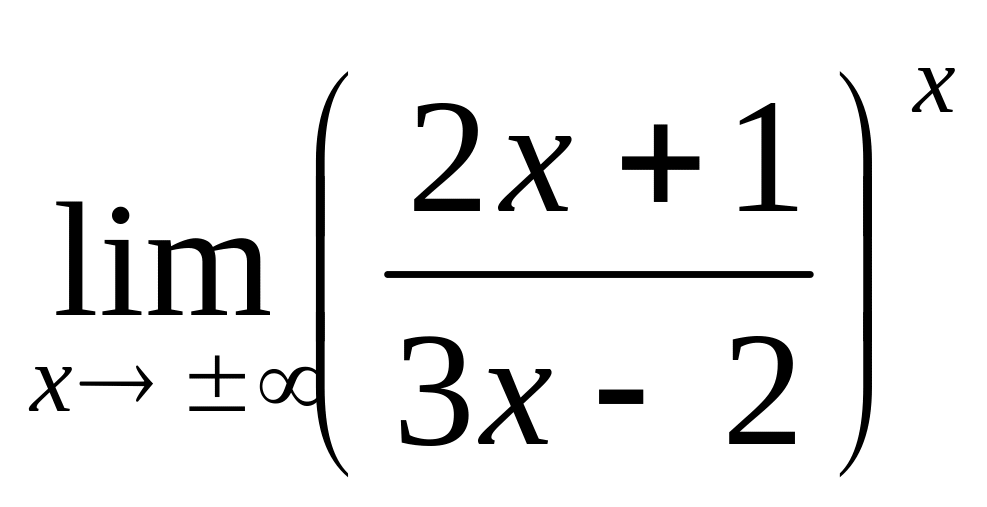
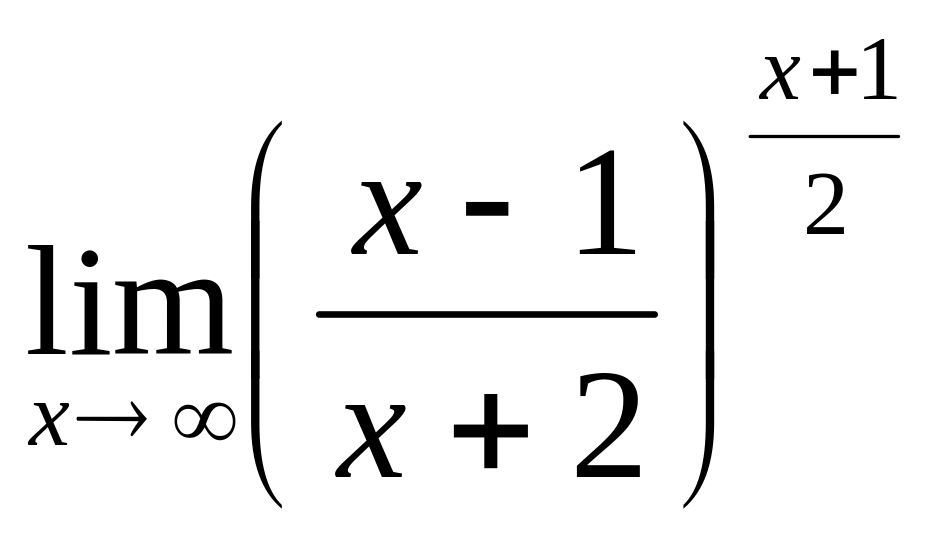Знайти локальні екстремуми та інтервали монотонності функцій:

28. 

29. ;

30. ;

31. ;

32. ;

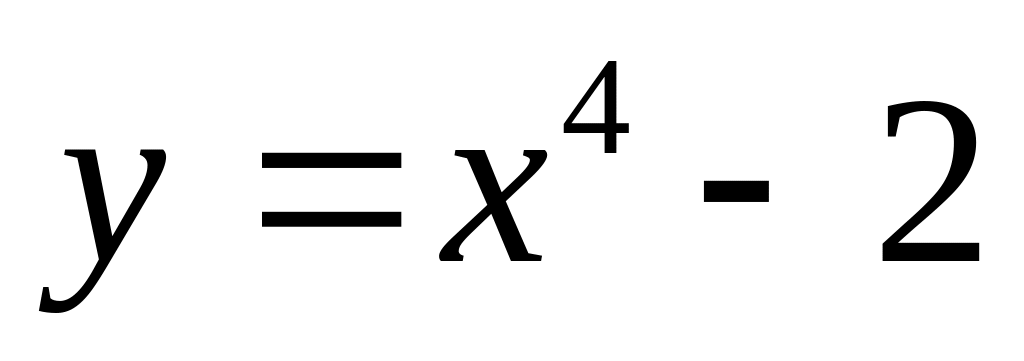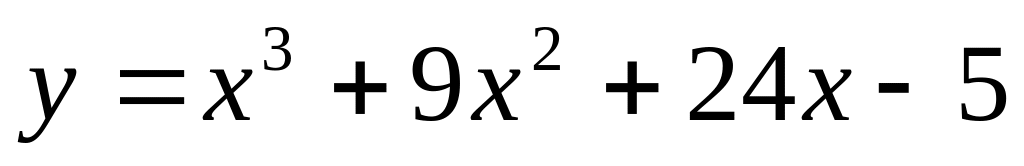Дослідити функцію на екстремум:

33. ;

34. ;

35. ;

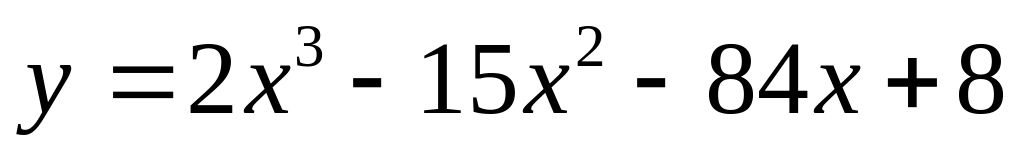Знайти найменше і найбільше значення функцій:

36. на відрізку ,

37. на відрізку ,

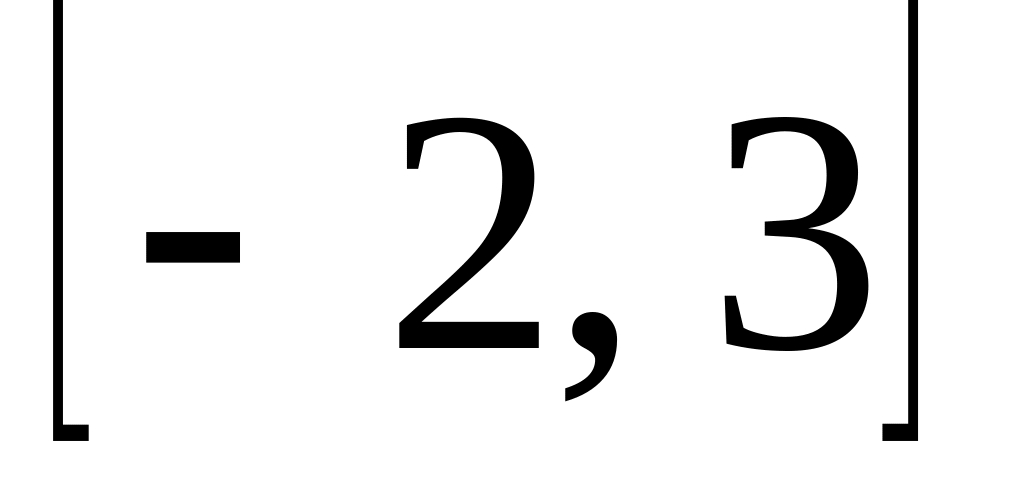38. на відрізку .

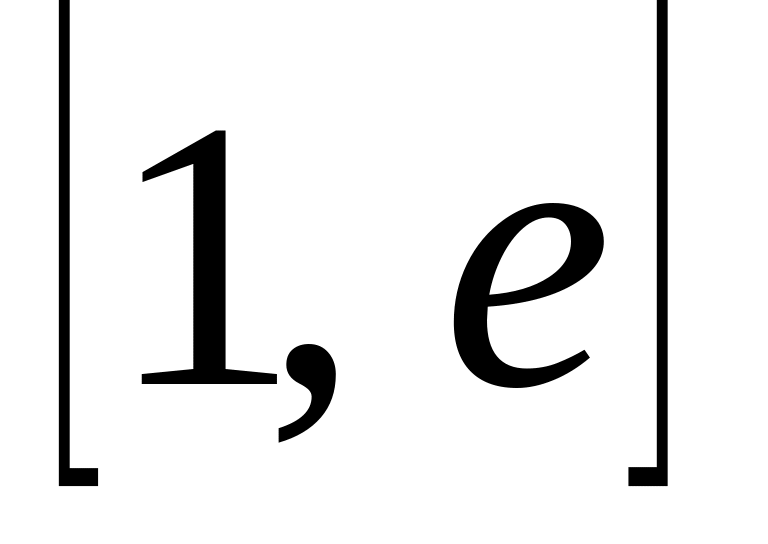Функції багатьох змінних

Встановити, чи є множина Е в просторі а) зв’язною, б) відкритою, в) областю:

39. ,

40. ,

Знайти область визначення функцій та зобразити її графічно:

41. ,

42. ,

43. .

Побудувати лінії рівня даних функцій:

44. ,

45. ,

46. .

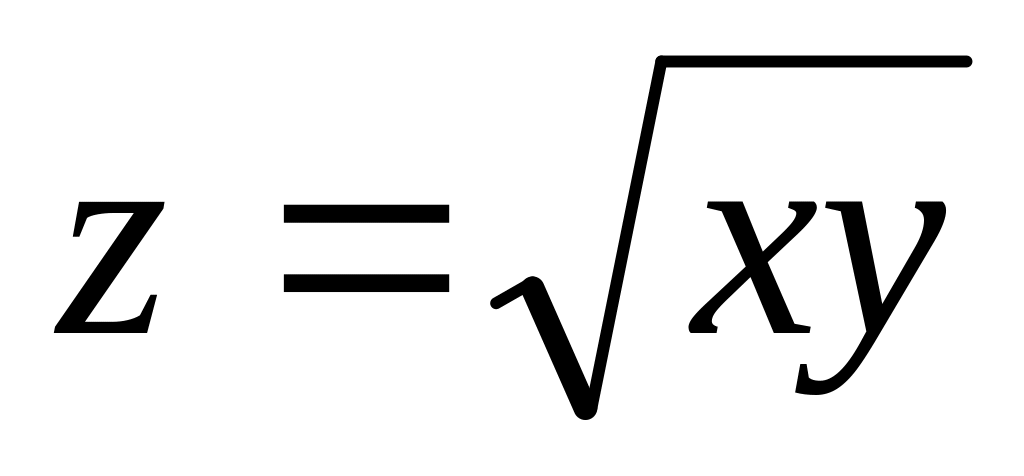Знайти усі похідні першого та другого порядків функцій:

;	;
;	.

Для заданих функцій у заданих точках знайти похідні за напрямом :

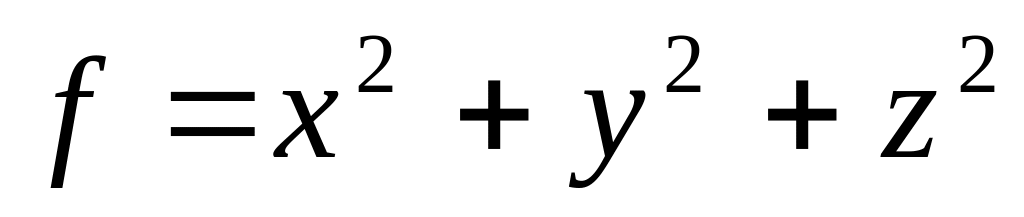, М(0, 1, 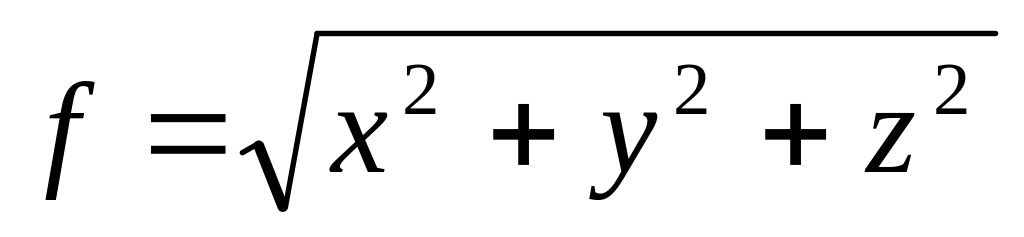1), ;	, М(1,1,1), ;
, М(1,0,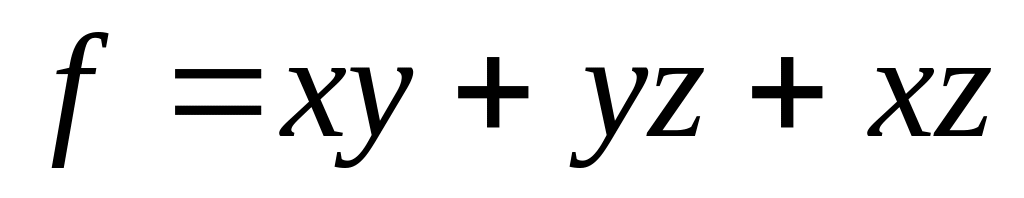1), ;	, М(1,1,1), ;.

Для заданих функцій знайти похідні за напрямом та градієнт в точці М0:

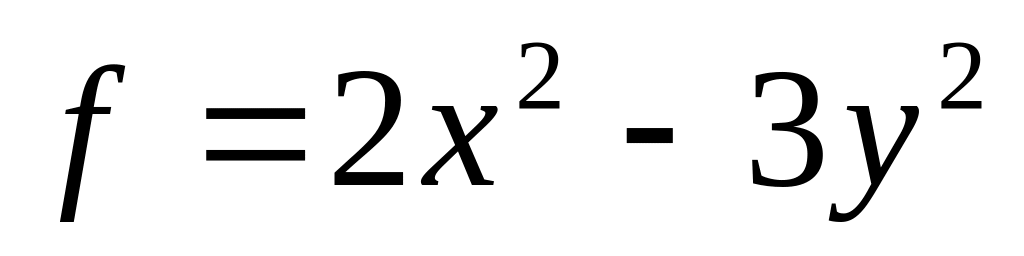55. , , М0(0,-2);

56. , , М0(1,-1);

57. , , М0(2,1);

Знайти повний диференціал функцій:

,	,
,	.

Для заданих функцій знайти і ідентифікувати стаціонарні точки:

,	,
,	.

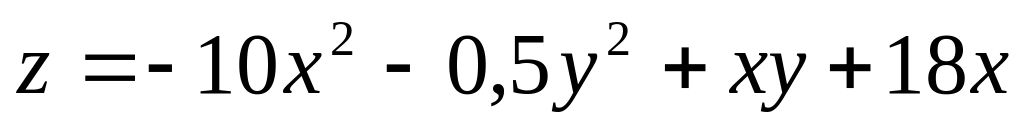Знайти екстремуми функцій:

,	,
,

Для заданих функцій і обмежень з допомогою методу Лагранжа знайти стаціонарні точки і ідентифікувати їх:

,	,
,	.

II. Інтеграли

1. Знайти первісну:

Застосовуючи підстановки (заміни змінної), знайти інтеграли:

Застосовуючи метод інтегрування частинами, знайти наступні інтеграли:

Застосовуючи формулу Ньютона-Лейбніца, знайти інтеграли:

Обчислити невласні інтеграли:

Побудувати рисунок та обчислити за допомогою визначеного інтегралу площу, утвореної фігури:

Інтегрування дробово-раціональних функцій

III. Диференціальні рівняння

Знайти загальний розв’язок або загальний інтеграл рівняння з відокремлюваними змінними:

;	;	;
;	;	.

Знайти загальний розв’язок лінійних диференціальних рівнянь першого порядку:

;	;	;
;	;	.