6.1.2. Невизначеність

Спроби класифікації невизначених явищ були неодноразово. Однією з найбільш удалих є класифікація, наведена на рис. 6.4.

Рис. 6.4. Основні види невизначеності

Однак, і вона, через відсутність єдиного підходу до визначення використовуваних понять далека від досконалості. Як видно з рисунка, до невизначеного пропонується відносити надзвичайно широкий спектр явищ, включаючи навіть нечітко-множинні лінгвістичні об'єкти.

С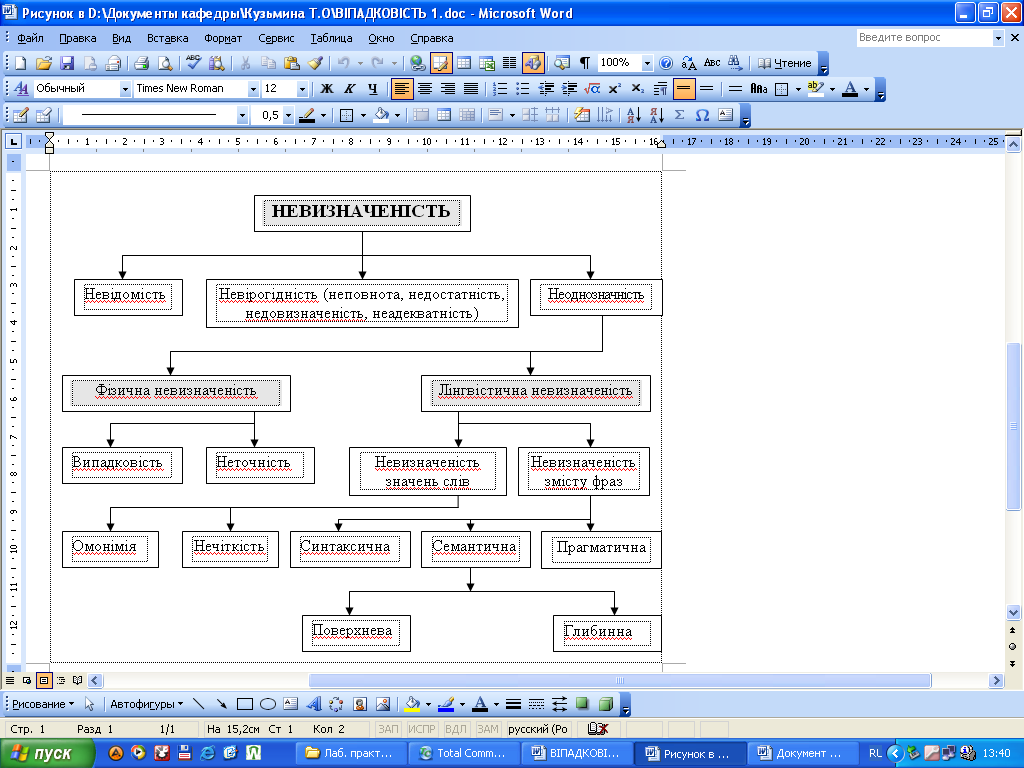 тановить інтерес трактування поняття невизначеності, що використовується в метрології. З доручення Міжнародного комітету мір і ваг (МКМВ) Міжнародним бюро мір і ваг (МБМВ) була створена робоча група з питання визначення невизначеності виміру. Ця робоча група підготувала рекомендацію INC-1 (1980) «Вираження експериментальних невизначеностей». В 1981 році на її основі МКМВ розробив рекомендацію 1 (З 1-1981). У розвиток цих рекомендацій під керівництвом ISO й при участі Міжнародної електротехнічної комісії (IEC), МКМВ і ряду інших міжнародних організацій розробленo «Посібник з вираження невизначеності вимірів».

У цьому керівництві відзначається, що на практиці існує «багато можливих джерел невизначеності при вимірі, включаючи:

1. неповне визначення вимірюваної величини;

2. недосконалу реалізацію визначення вимірюваної величини;

3. нерепрезентативну вибірку – обмірюваний зразок може не представляти обумовлену вимірювану величину;

4. навколишнього середовища, що впливають на вимір або недосконалий вимір умов навколишнього середовища;

5. суб'єктивну систематичну погрішність оператора при знятті показань аналогових приладів;

6. кінцеву розв'язну здатність приладу або межу чутливості;

д) неточні значення, приписані еталонам, які використовуються для виміру, і стандартним зразкам речовин і матеріалів;

h) неточні значення констант і інших параметрів, отриманих із зовнішніх джерел і використовуваних в алгоритмі обробки даних;

і) апроксимації й припущення, що використовуються в методі виміри й вимірювальній процедурі;

j) зміни в повторних спостереженнях вимірюваної величини при однакових умовах.

Ці джерела не обов'язково є незалежними й деякі із джерел від а) до і) можуть вносити вклад у джерело j)».

На жаль, вірно відмічені джерела невизначеності реально або взагалі не враховуються керівництвом і іншими документами, що його розвивають або підмінюються випадковими. Розроблювачі цих документів не вловили головного, що ділення на детерміновані й випадкові явища, не коректно.

Взагалі, невірно розглядати випадковість як протилежність детермінованості. Вірніше ділити множину явищ на детерміновані й на недетерміновані, тобто невизначені.

6.1.3. Оцінка невизначеності вимірів під час проведення випробувань

У зв'язку з процесами інтеграції до ЄС, входження України у світовій ринок, стають актуальними питання оцінки відповідності продукції міжнародним чи національним стандартам. Особливої уваги вимагає проведення випробування, як інструмент оцінки відповідності. Вихідною процедурою під час проведення випробувань є вимірювання.

В Україні запроваджено національний міжнародний стандарт ДСТУ ISO/IEC 17025 «Вимоги до компетентності випробувальних та калібрувальних лабораторій», який законодавчо закріпив необхідність наявності (застосування) процедури оцінювання невизначеності вимірів (а саме оцінка точності отриманих результатів), які проводяться у лабораторіях, які претендують на міжнародне визнання своїх результатів вимірів.

Невизначеністю вимірів називається параметр, який пов'язаний з результатом вимірів та характеризує розсіювання значень, які можна обгрунтовано приписати вимірюваній величині. Існує два способа А та В оцінки невизначеності:

А – складові, оцінювані шляхом застосування статистичних методів (наприклад, обробка результатів багатократних вимірів);

Б – складові оцінювані не статистичним способом (за характеристиками, узятими з попередніх експериментів з паспорта на прилад, методик виконання вимірів, довідників тощо.). До джерел цих невизначеностей відносяться: випадкові похибки однократних вимірів; поправки, запроваджувані в результати виміру, не виключені систематичні похибки довідкових даних та ін.

При математичній обробці багатократних вимірів вирішують дві задачі. Перша задача вирішується способом А, при цьому визначається деяке близьке значення У вимірюваною величини, назване оцінкою і найкращим чином відповідає отриманим результатам. При рішенні задач другим способом Б визначають експериментальну стандартну невизначеність результатів окремих спостережень U результату вимірів.

При статистичної обробці результатів проводилися такі операції:

1) Виняток із числа результатів спостереження результатів, які мають грубі промахи і систематичні похибки;

2) Обчислення середнього арифметичного за групами відкоректованих результатів:

(6.1)

де К – число вимірів в групі; Р_рі – навантаження при розриві, Н.

3) Знаходимо найкращу оцінку вимірюваною величини , як середнє арифметичне

(6.2)

де J – кількість груп.

4) Визначення оцінки внутрішньо групової дисперсії S_s²:

(6.3)

5) Знаходимо експериментальну дисперсию середніх арифметичних груп. Така оцінка одна.

(6.4)

6) Визначаємо дві незалежні оцінки усередненій внутрішньогруповий дисперсії спостережень:

(6.5)

має кількість ступенів свободи J-1;

(6.6)

має кількість ступенів свободи J(K-1)

7) Визначаємо розрахункове значення критерію Фішера за такою формулою:

(6.7)

Критичне значення F для ймовірності 0,95 при числі ступенів свободи знаходимо за таблицею, F_табл.. Якщо F_розр. < F_табл, існування міжгрупової похибки заперечується і однорідність зразків вважається задовільною. Оцінену дисперсію визначаємо:

(6.8)

має кількість ступенів свободи J -1.

Розширена невизначеність (U) результату вимірювань розраховується за такою формулою:

U=tp S

(6.9)

де t_p – критерій Стьюдента.

Розширена невизначеність, як інтервальна оцінка результату вимірів, характеризує розсіювання значень, які можуть бути обґрунтовано приписані вимірюваній величині.